| 【問1】 表のような定格を有するA、B2台の三相変圧器を並行運転して、三相負荷に電力を供給している。変圧器の一次側に60〔kV〕の電圧を加えた場合、次の問に答えよ。ただし、負荷は供給電圧が
6.6〔kV〕のとき消費電力が6 000〔kW〕の抵抗負荷とし、また変圧器励磁電流および巻線の抵抗は、無視するものとする。 (1) 変圧器に流れる循環電流はいくらか。 (2) A変圧器の二次側の断路器を解放して、負荷をB変圧器のみに持たせた場合、開放した断路器の極間電圧はいくらか。
|
〔解き方〕
(1) A変圧器のリアクタンスXA 〔Ω〕、B変圧器のリアクタンスXB
〔Ω〕とすると、
XA=(%XA )×![]() = 0.595〔Ω〕
= 0.595〔Ω〕
XB=(%XB )×![]() =
0.952〔Ω〕
=
0.952〔Ω〕
A,B両変圧器の二次側に誘起される相電圧をEA 〔kV〕,EB 〔kV〕とすると、
EA=![]() =3.92
〔kV〕
=3.92
〔kV〕
EB=![]() =3.79 〔kV〕
=3.79 〔kV〕
A,B両変圧器の内部誘導起電力は同相であるので、これらの差は、
3.92−3.79=0.13 〔kV〕= 130〔V〕
循環電流をI C とすると、
I C=![]() =84.0 〔A〕 ・・・・・〔答〕
=84.0 〔A〕 ・・・・・〔答〕
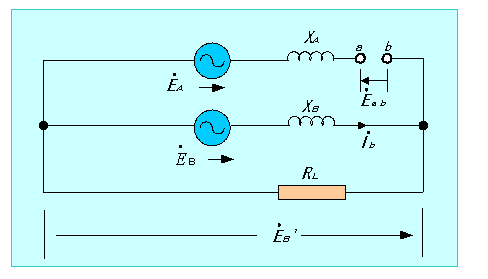
(2) 問題の回路を1相分について描くと図のようになる。
RL=
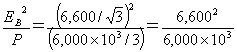 =7.26〔Ω〕
=7.26〔Ω〕 B変圧器の端子電圧
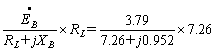
= 3.73−j0.488 〔kV〕
また、A変圧器は無負荷であるので、内部誘導起電力はそのまま端子電圧となって現れる。したがって、断路器の極間電圧
=3.92−(3.73−j0.488)=0.19+j0.488
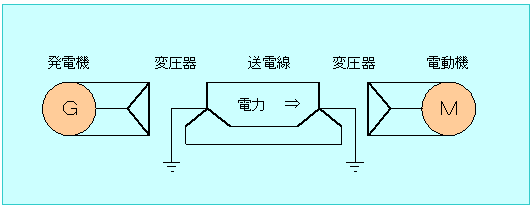
| 【問2】図の送電系統において、送電線に次の事故が発生したとき、送電電力が事故前の何分の1になるかを求めよ。
(1) 任意の地点で1線地絡事故が発生した場合 (2) 任意の地点で2相短絡事故が発生した場合 (3) 任意の地点で2線地絡事故が発生した場合 |
〔解き方〕
送電電力は、回路の抵抗、静電容量を無視できる純リアクタンス回路の場合、次式で表される。
P=![]()
ただし、P:送電電力,VS:送電端電圧,Vr:受電端電圧,
xa,xb;故障点からVSおよびVr側を見た正相リアクタンス
δ;送電端電圧と受電端電圧との位相差(相差角)
地絡あるいは短絡事故の場合の等価回路は図のとおりで、事故の種類に応じてxCを挿入することによって事故前後の送電電力を計算できる。
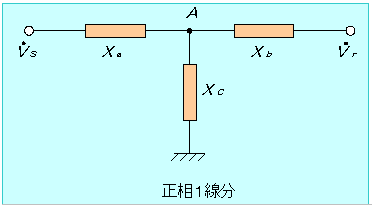
・1線地絡の場合;xC=x0+x2
・2相短絡の場合;xC=x2
・2線地絡の場合;xC=
と表すことができる。
事故直後の送受電端電圧間の相差角は、発電機回転子の慣性が非常に大きいので事故前とほとんど変化しない。
よって、事故直後の送電電力P 'は、
P'=
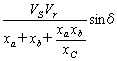
したがって、事故後の送電電力の比(P '/P)は、

となる。
また、題意より事故点から見た零相、正相、逆相リアクタンスがおのおの相等しいので、
x0=x1=x2=
である。
したがって、
(1) 1線地絡の場合
xC=x0+x2=
∴
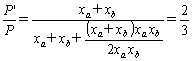 ・・・・・〔答〕
・・・・・〔答〕(2) 2相短絡の場合
xC=x2=
∴
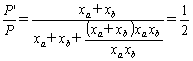 ・・・・・〔答〕
・・・・・〔答〕(3) 2線地絡の場合
xC=
∴
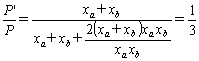 ・・・・・〔答〕
・・・・・〔答〕以上の結果から、いずれの場合もリアクタンス値には無関係で一定となり、事故点の位置には影響されない。