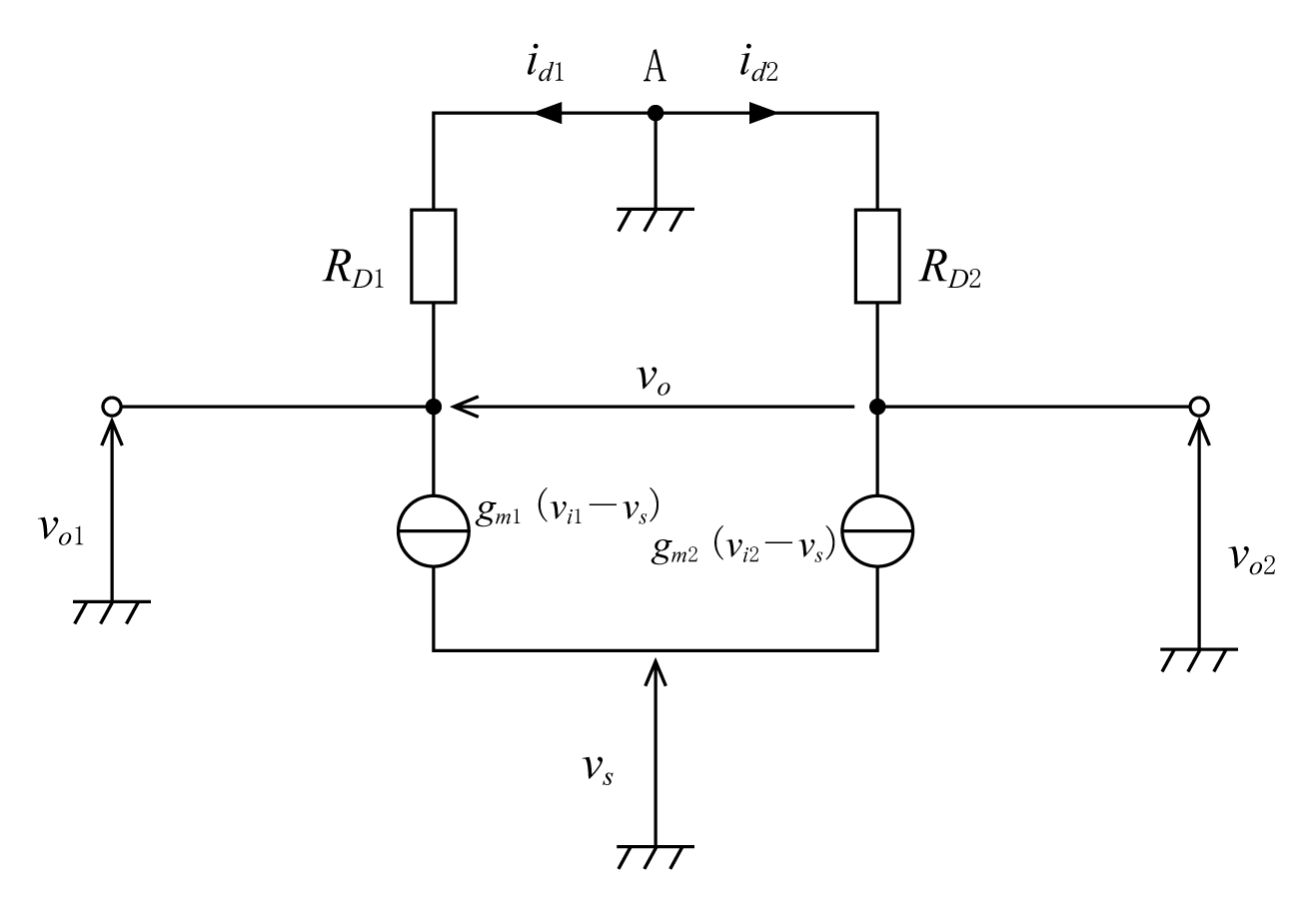〜終わり〜
■ぜひアンケートにご協力下さい■


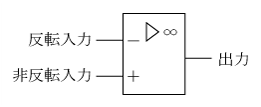
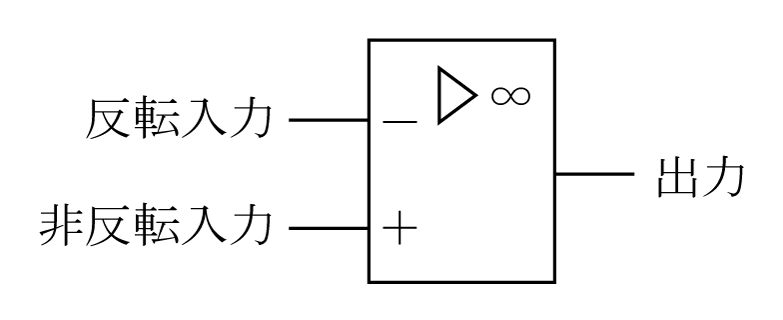
オペアンプはoperational amplifierの略称で、演算増幅器とも呼ばれている。オペアンプは第1図に示す図記号で表され、二つの入力端子と一つの出力端子を備えている。
オペアンプの二つの入力端子は、それぞれ反転入力端子と非反転入力端子と呼ばれている。また、オペアンプには一般に正電源及び負電源の二つの直流電源が入力される電源端子が設けられている(第1図には示していない)。
理想的なオペアンプにおける二つの入力端子間のインピーダンス、すなわち入力インピーダンスは、∞〔Ω〕、出力インピーダンスは、0〔Ω〕である。また、電圧増幅度(電圧利得)は無限大であり、周波数特性は0〔Hz〕(直流)〜∞〔Hz〕である。
これらの数値はあくまで理想値であって、実際のオペアンプとは異なっている。例えば、長い間にわたって汎用的に使用されているμA741シリーズのオペアンプの特性は、第1表に示すようになっている。理想的なオペアンプほどではないものの入力インピーダンスと電圧増幅度が大きい一方、出力インピーダンスは極めて小さいことが分かる。
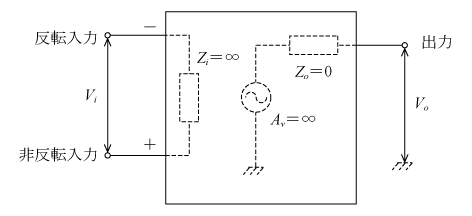
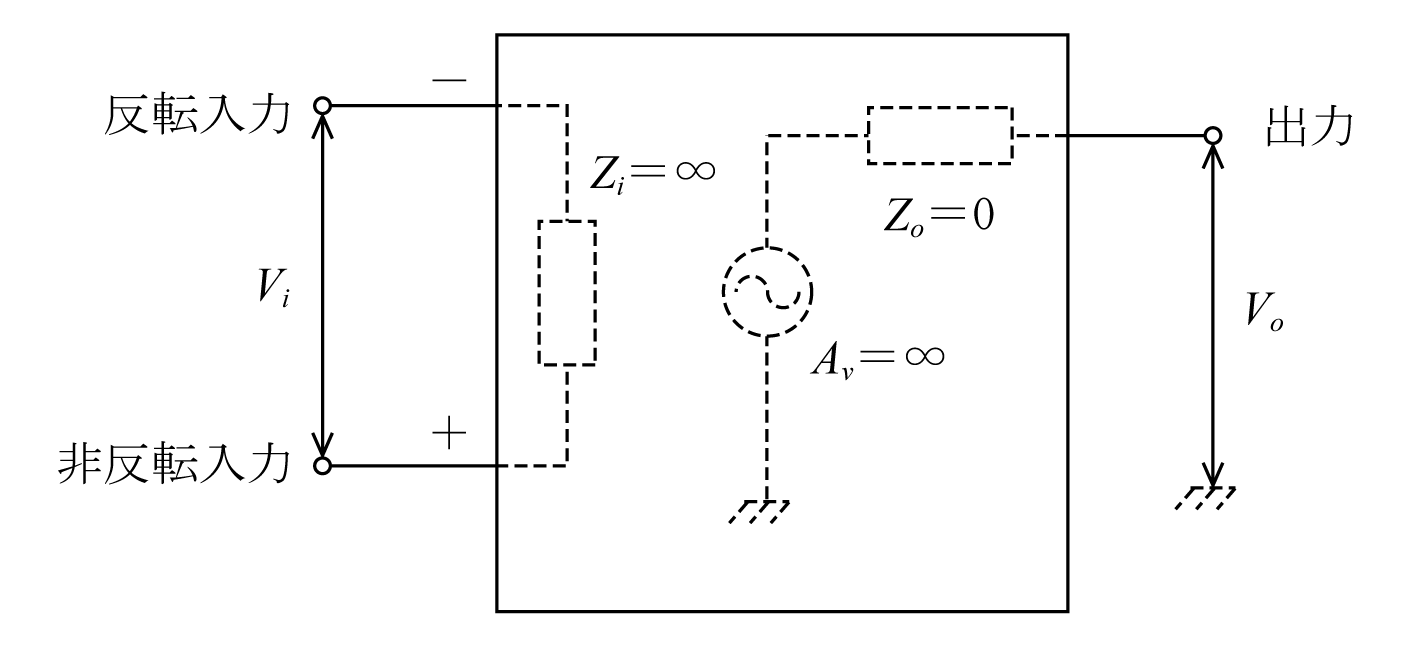
このような特性のオペアンプは、第2図の等価回路に示されるように差動増幅器の二つの入力端子をそれぞれ反転入力端子および非反転入力端子とし,この差動増幅器の出力端子に現れる差動電圧出力を無限大になるまで増幅した回路と考えることができる。
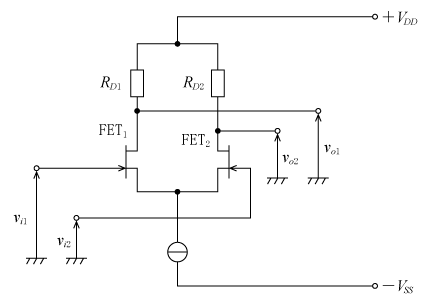
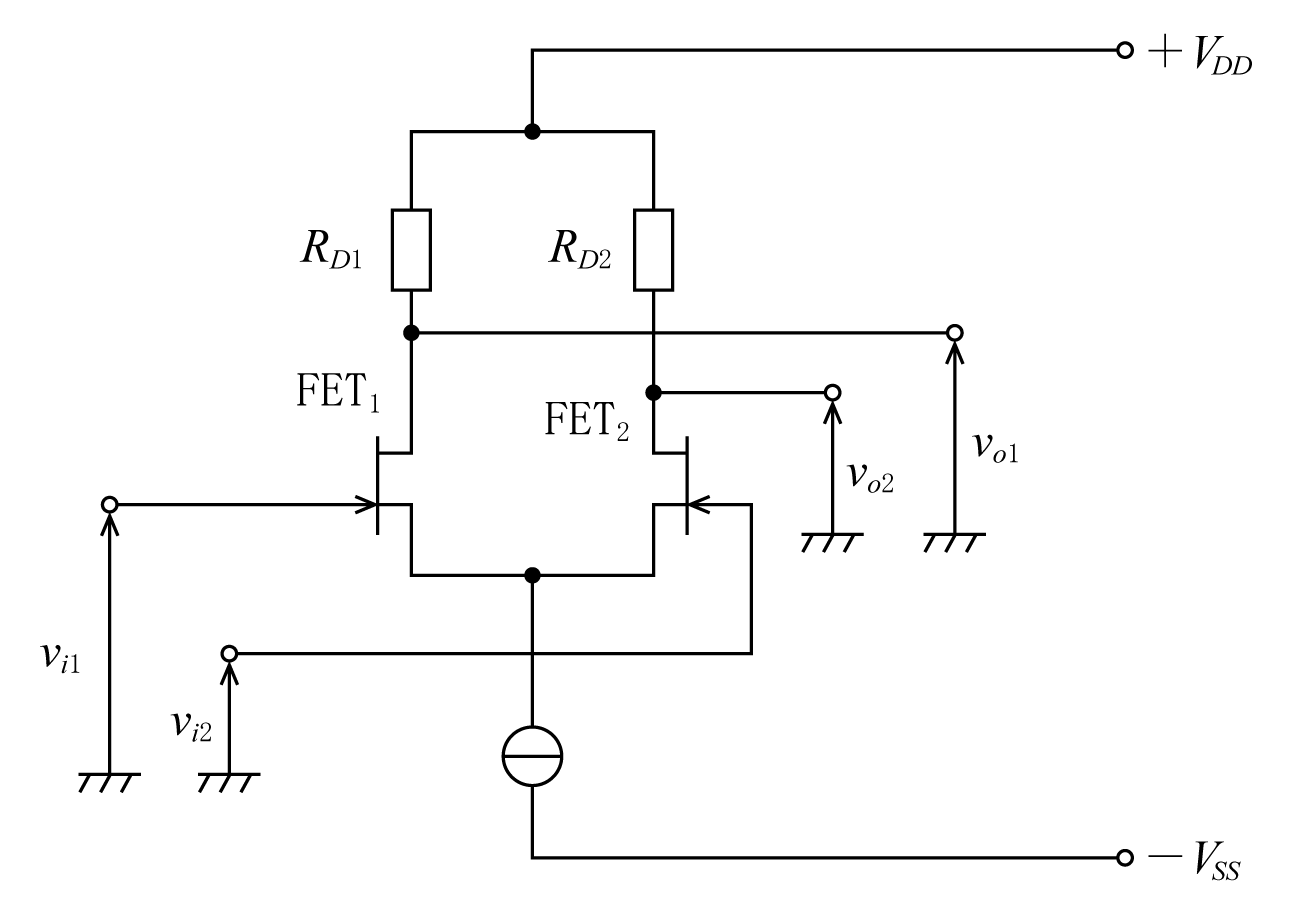
オペアンプを構成する差動増幅器について解説する。例えば、FET(電界効果トランジスタ)を2個用いて構成した差動増幅回路の一例を第3図に示す。二つのFETのゲートがそれぞれ差動増幅回路の入力端子(反転入力端子及び非反転入力端子)であり、また二つのFETのドレインが出力端子である。
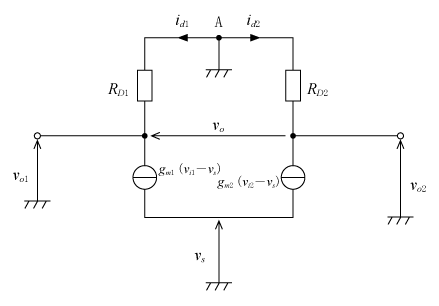
ここでFETの出力インピーダンスrdがドレインに接続された抵抗RD1,RD2に比べて十分大きいと仮定する。すると差動増幅回路の小信号等価回路は第4図に示すようになる。
この等価回路でFETのソース端子は非接地となっている。これは入力端子に与えられる入力信号(交流信号)が直流定電流源に流れないため交流的にみれば非接地と等価なためである。
さて、FET1及びFET2のドレイン電流をそれぞれid1及びid2とすれば、出力端子の電圧vo1,vo2は、それぞれ次式に示すようになる。
各FETの相互アドミタンスをgm1,gm2とし、ソース端子の電圧をvsとすれば、ドレイン電流id1,id2は、
と求まる。また、点Aにおける電流はキルヒホッフの電流則から次式となる。
ここで,RD1= RD 2= RD,gm1= gm2= gmとすれば、(1)〜(5)式から次式が導かれる。
次にvo1とvo2の差電圧voを求めれば、
となる。この差電圧voを差動出力電圧という。また、
![]()
![]() は二つの入力端子の差電圧であり、差動入力電圧と呼ばれている。
は二つの入力端子の差電圧であり、差動入力電圧と呼ばれている。
差動増幅回路はこのように二つの入力端子に与えられた電圧の差を増幅し、その結果として二つの出力端子間に差電圧として出力するようになっている。
差動増幅回路を構成する回路要素は、周囲温度の変化によってその特性が変化する。特にFETは周囲温度の変化の影響を受けやすくドレイン電流の変化となって現れる。しかし、FET1とFET2の温度特性が等しいとすれば、周囲温度の変化によるid1及びid2の変化量も等しくなる。更にVGSの変化もFET1、FET2で同様に変化するため差動電圧出力は、周囲温度の変化を受けることがない。
したがって、差動増幅器は温度変化による特性変化の影響を受けることなく、安定した動作をすることができる。