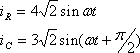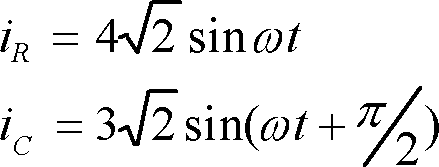1　加法定理が基本

　〔例題1〕　第1図の回路で

とすると、合成電流iおよび、その実効値を求めよ。

■第1図■

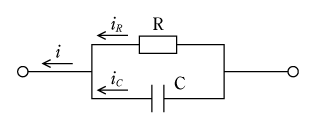
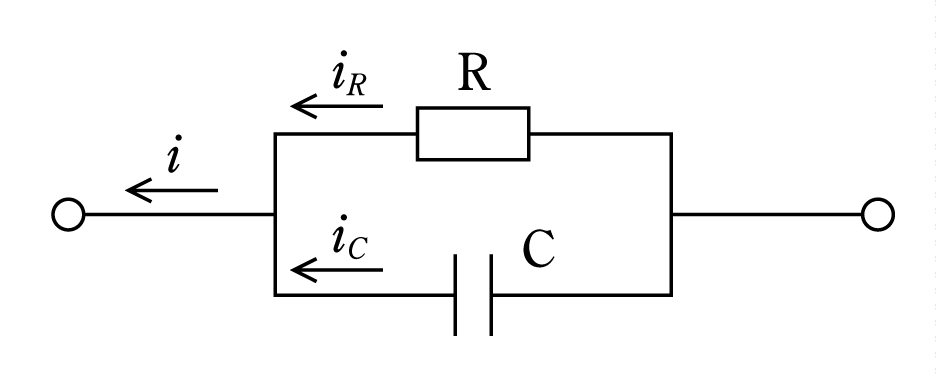
　〔解答〕　解答を手がけるとまず最初に壁にぶつかるのは

　ここでは三角比から発展したいくつかの公式が使えないとどうしようもなくなる。正解例を示すと次のようになる。

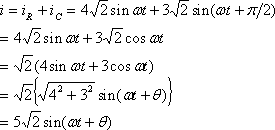
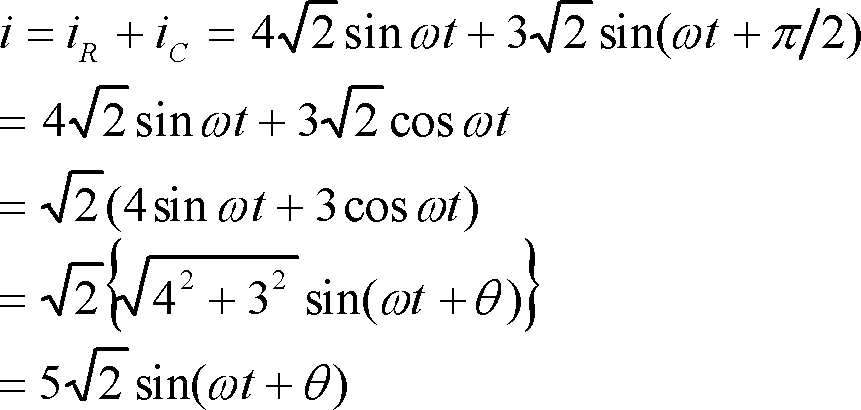
　また、合成電流の実効値Iは、最大値が であるからI=5Aとなる

　さて、この例題1ではいくつかの式の変形を行なっているが、主なものは次の2項目である。

　(1)　sinが だけずれればcosになる。

　(2)　 を適用する。ただし

　この公式は瞬時値の和などに使う公式であるが、どうしてこの式が成り立つかについてはこのあとの加法定理を用いて証明できる。加法定理についてはこの公式ばかりではなく、いろいろな公式の基礎になっているので、しっかりつかんでいてほしいと思う。

2　加法定理を知れば、あとの公式はいもずる式に導かれる

　この定理は二つの角の和や差の三角関数すなわち

　　 がどんな式で表わされるかを示したものである。

　　〔加法定理〕　　　　　　　　　　　　　　　　　　　（複合同順）　

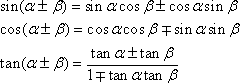
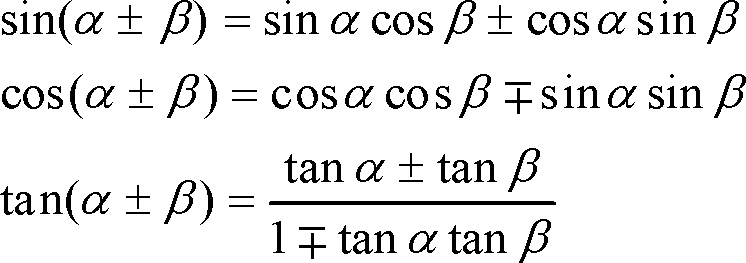
3　加法定理の証明をおぼえよう

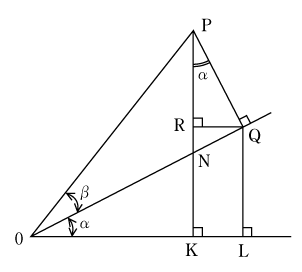
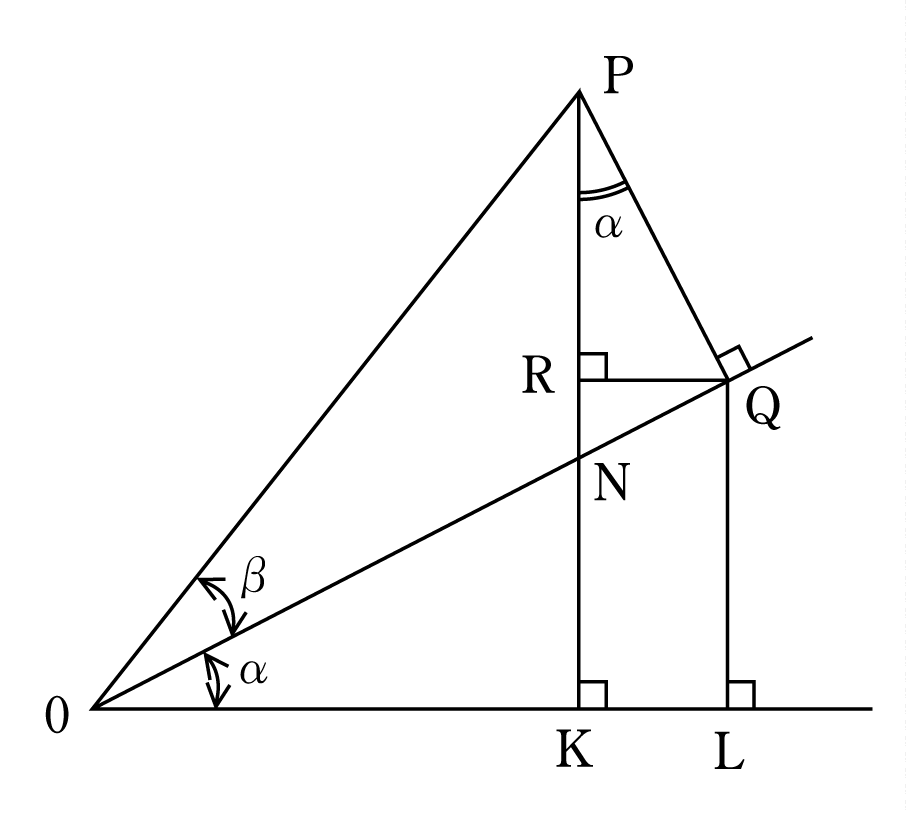
　第2図でαとβの二つの角の和の三角関数 を求めてみよう。

　（着眼点）

　第2図において、三つの三角形△PQO,　△PQR、△QOLのそれぞれについて

　 　がどんな辺の比で表わされるかをしっかりつかむことが大切である。ここで、∠QOK=α、△ONK∽△RNQ（相似）であることから、∠RQN=αとなり、さらに∠QPR=αとなることがわかる。

　ここでちょっとテクニックを使う。前の項の分母、分子に を、後の項の分母、分子に をかけると、

■第2図■

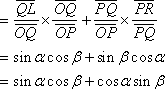
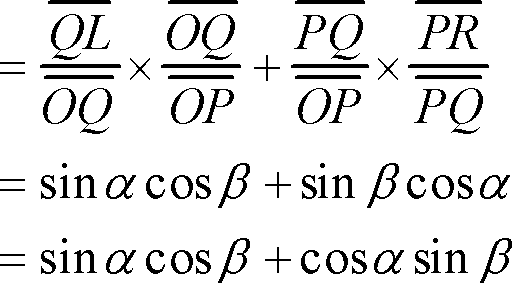
　また　

　ここで前と同じように分母、分子に をかけて

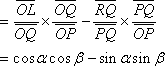
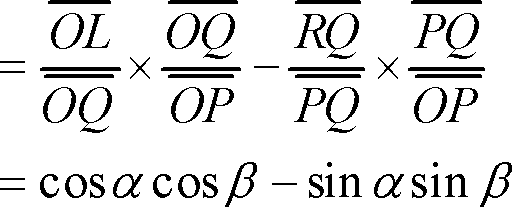
　以上のように、 および だけ記憶しておけば、あと積や和の公式は、この加法定理を変形していくだけで導くことができる。変形のしかたはつぎのように行えばよい。

　 　　　左式の右辺において

　 であるから、βのかわりに―βとおけば

　　　 　　　が得られる

　公式の右辺の組み合わせをよく見ると、sinの場合はサインコスコスサイン、またcosの場合はコスコスサインサインのように覚えやすい組み合わせになっていることに気がつくと思う。

4　加法定理をもちいた証明問題

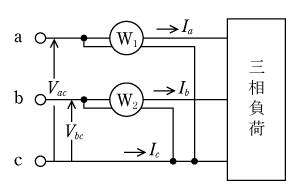
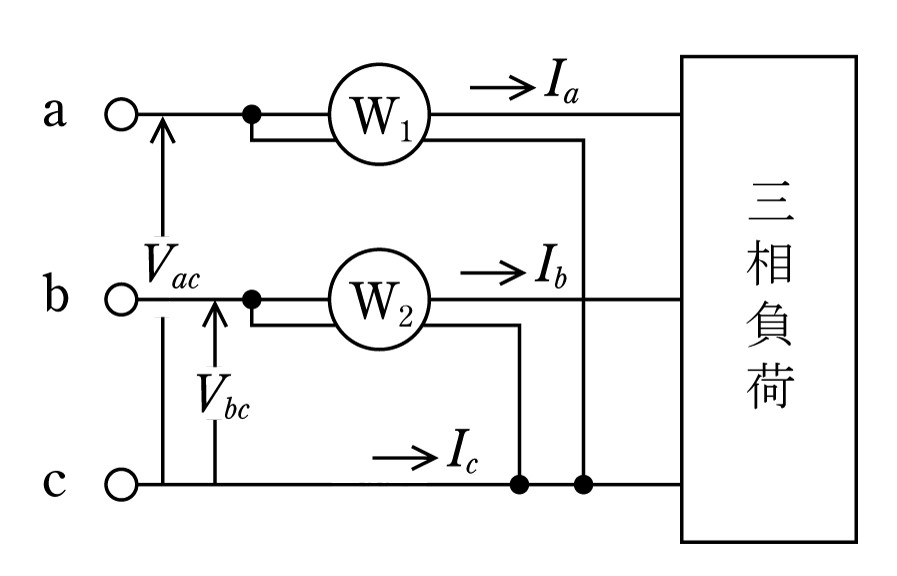
　〔例題2〕第3図の対称三相回路において、

　ac間にW₁、bc間にW₂の単相電力計を

　2個接続したとき、電力計の指示の和は

　負荷の三相電力を示すことを証明せよ。

　　ただし、負荷の力率をcosθとする。　　　　　　

■第3図■

　〔解答〕

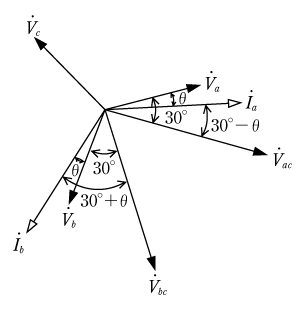
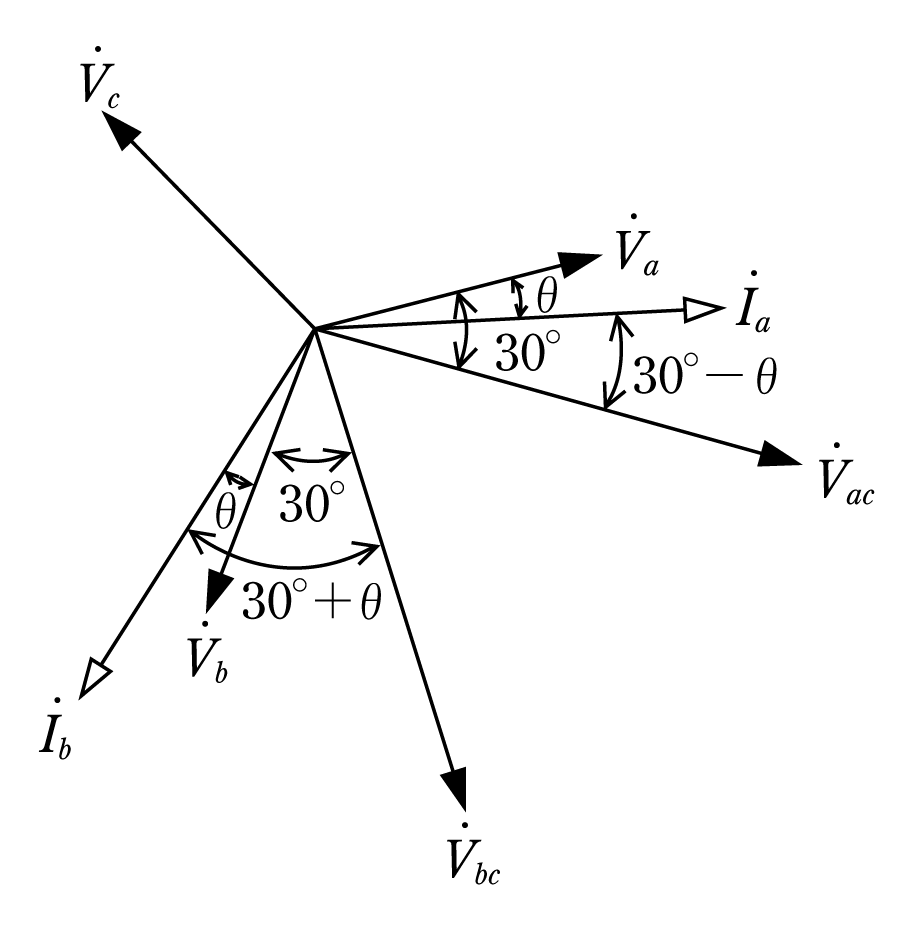
　相電圧を　 　線電流を　 　とするとベクトル図は第4図のようになる。W₁、W₂の指示をP₁、P₂　とすると

■第4図■

　ベクトル図より　　　

とすれば　加法定理によって展開し

　 　が得られる。

　これは三相電力を測定するための電力計は2個でよいことを示す（ブロンデルの定理という）

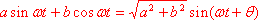
5　 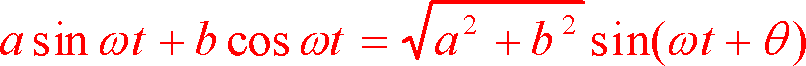の証明

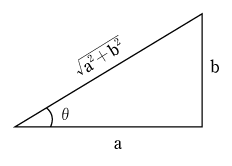
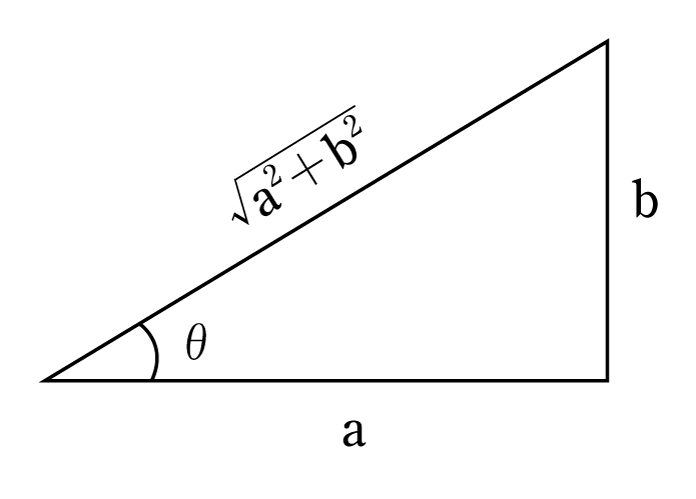
　例題1で用いたこの式の一体どこから が出てきたのか考え込んでしまうかもしれないが、これも加法定理をうまく利用しようという考えから出ている。一方がsin（正弦）で他方がcos（余弦）なので第5図のような直角三角形を念頭に置き、加法定理を使ううえで、 を下記のように をくくり出した式をつくる。

■第5図■

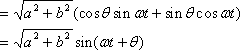
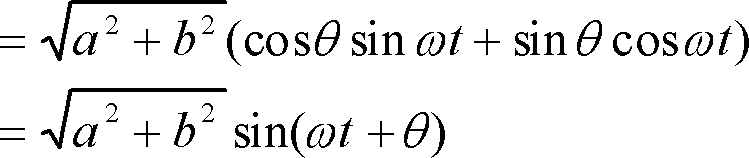
　結果を見れば、じつに簡単な形にまとまっていますが、要点は加法定理が使えるような形に式を変形したわけである。

6　公式は自分で作れる

　加法定理

　　

　　

において　α=β　とすれば、2倍角の公式が得られる

　また加法定理

において、上記の公式 と の和および差をつくれば次の公式が得られる

　同様に　 と の和および差をつくれば次の公式が得られる

　これらは積から和への公式となるものであるが、そのほか和から積の公式などこれらを変形することで求めることができる。三角関数は公式が多くて面白くないと思うかもしれないが、公式に振り回されるのではなく、公式を振り回すような積極的な姿勢で取り組んで欲しいと思う。