〜終わり〜
■ぜひアンケートにご協力下さい■


三角関数の加法定理を用いると、数多くの一連の関連公式を導出することができる。正弦波交流電圧の実効値の算出、平衡三相回路の各相電流和が0になることの証明、有効電力の公式の導出などを例題として、これらの関連公式をどう生かすかを解説する。
〔例題1〕 正弦波交流電圧
![]()
![]() の実効値Eは、
の実効値Eは、
![]()
![]() で示されることを証明せよ。
で示されることを証明せよ。
(解答)実効値の定義が、瞬時値の二乗の平均の平方根であることを知っていればそのとうりに三角関数の関連公式を展開していけばよい。
解きかたの順序
① 瞬時値
![]()
![]() を二乗すると
を二乗すると
![]()
![]()
② ①式の
![]()
![]() の部分を、下記の2倍角の公式に置き換える
の部分を、下記の2倍角の公式に置き換える
〔2倍角の公式〕
![]()
![]() よって
よって
![]()
![]()
③ よって瞬時値の式は
![]()
![]()
![]()
![]()
④ ③式の平均を求めるとマイナスの部分
![]()
![]() は1〔Hz〕の平均をとると0になる。
は1〔Hz〕の平均をとると0になる。
⑤ 結局③の平方根を求めると実効値Eは
![]()
![]() E=
E=
![]()
![]()
〔例題2〕平衡三相交流回路において、各相を流れる電流
![]()
![]()
![]()
![]()
![]()
![]() の和は
の和は
![]()
![]()
になることを証明せよ。
(解答)三角関数の関連公式を用いて、この証明をするためには、和を積になおす公式を使う必要があり、この公式を知らなければ答はオジャンになってしまう。しかし心配はいらない。加法定理にもどって公式をつくり直せばよい。ひとまず、この問題を解くための手順を示し、解答を求めることにしよう。
解きかたの順序
① まず
![]()
![]() を求める。
を求める。
![]()
![]()
② 和を積に直す公式(下記)にあてはめて、①式を変形する。
③
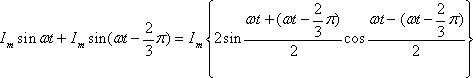
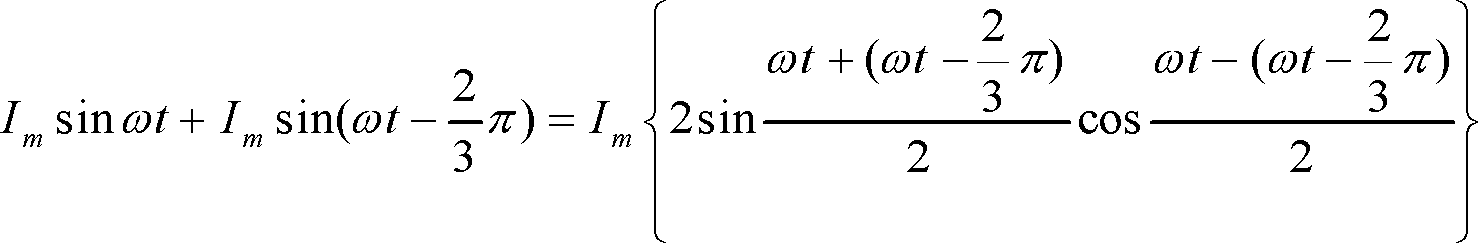
この式で
![]()
![]() だから
だから
![]()
![]()
④
![]()
![]() の結果に
の結果に
![]()
![]() をたす
をたす
![]()
![]()
![]()
![]()
ここで
![]()
![]() であるから
であるから
![]()
![]() となる
となる
上の2式を左辺どうし、右辺どうし加えると
ここで
![]()
![]() 、
、
![]()
![]() と置いてみればこの二つの式から
と置いてみればこの二つの式から
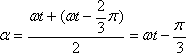
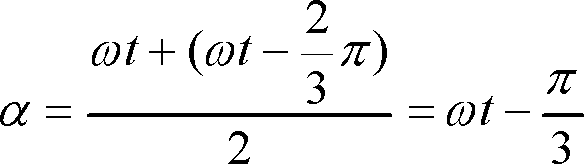
![]()
![]()
となるから、したがって
ここで
![]()
![]() であるから
であるから
となって
![]()
![]() の結果と同じになることがわかる。
の結果と同じになることがわかる。
たくさんある公式をみな覚えていることはよいが、あやふやな記憶に頼るくらいなら、やや遠まわりでも以上のように加法定理に一度もどって確かめることも良い。
解きかたの順序
① 電力の瞬時値を示す
② ①の式は積の形になっているので、積を和に変換する。
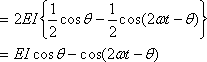
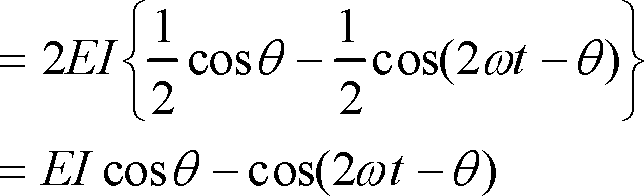
ここで括弧の2項目の
![]()
![]() は1〔Hz〕の平均をとると0のなるので電力の平均値Pは
は1〔Hz〕の平均をとると0のなるので電力の平均値Pは
P=EIcosθ〔W〕 となる。
例題3の積を和に変換した公式は、つぎの余弦の加法定理の操作によって得られたものである。
(2)式から(1)式を引くと
したがって
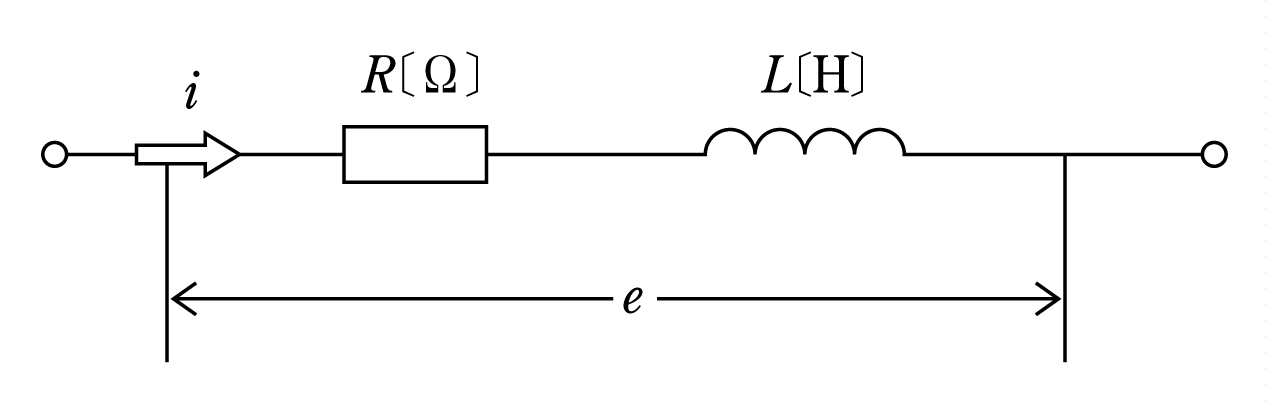
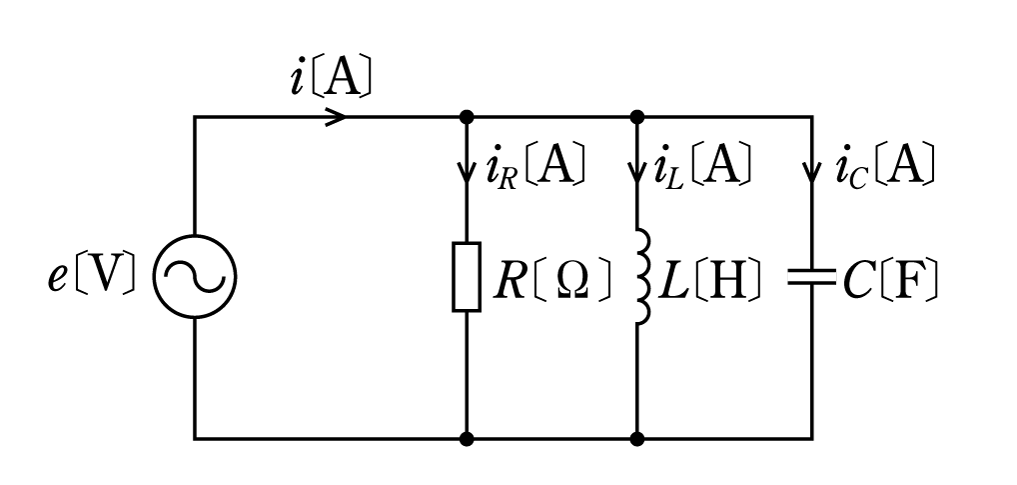
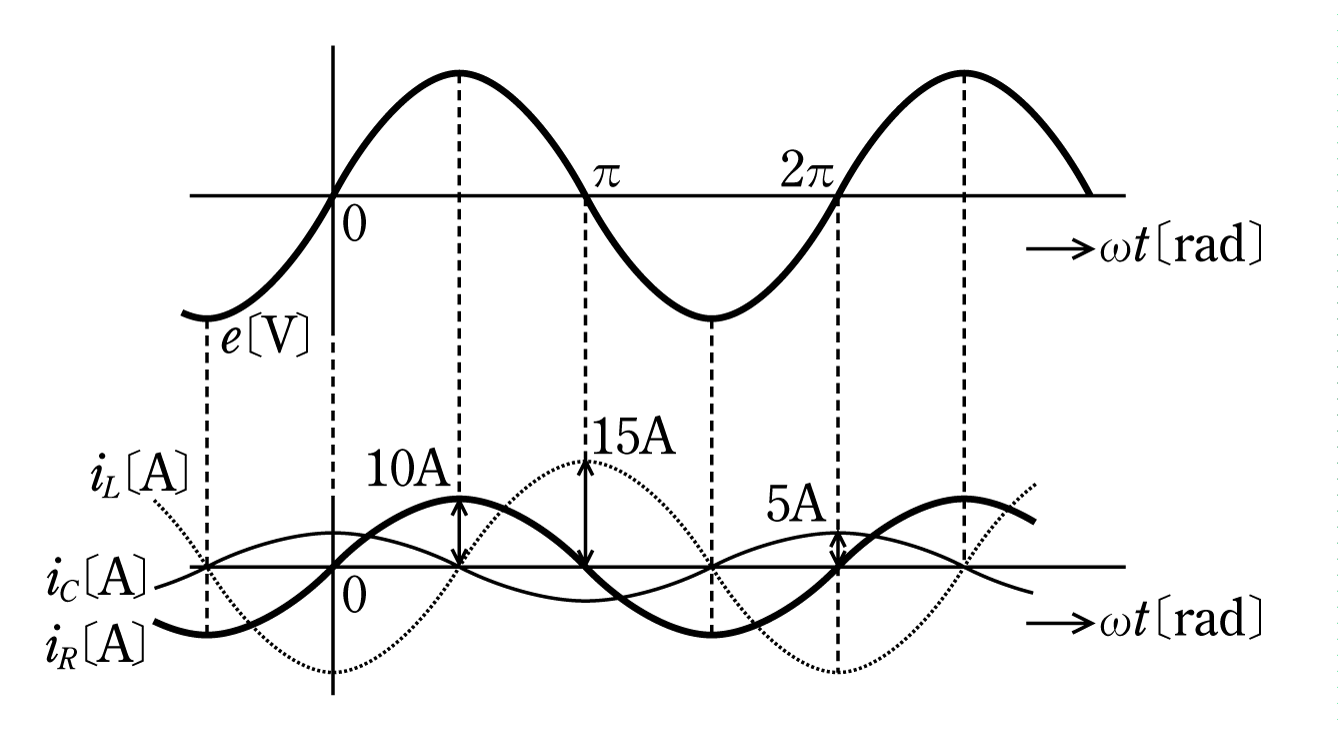
〔例題4〕第2図のように、R〔Ω〕の抵抗、インダクタンスL[H]のコイルおよび静電容量C[F]のコンデンサを並列に接続した回路がある。 この回路に正弦波交流電圧e[V]を加えたとき、この回路の各素子に流れる電流
![]()
![]() とe[V]の時間的変化はそれぞれ第3図のようで、それぞれの電流の波高値は10A,15 A、5Aであった。回路に流れる電流i[A]の電圧
とe[V]の時間的変化はそれぞれ第3図のようで、それぞれの電流の波高値は10A,15 A、5Aであった。回路に流れる電流i[A]の電圧
e[V]に対する位相として正しいのはつぎのうちどれか。
(1)30°遅れる (2)30°進む (3)45°遅れる
(4)45°進む (5)90°遅れる
解答と解説
各素子を流れる電流の瞬時値の和を求め加法定理を応用する。
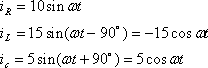
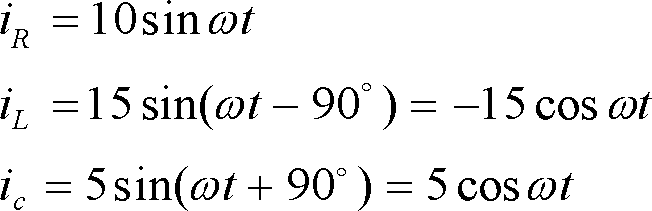
したがって
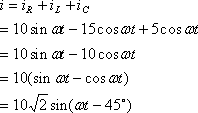
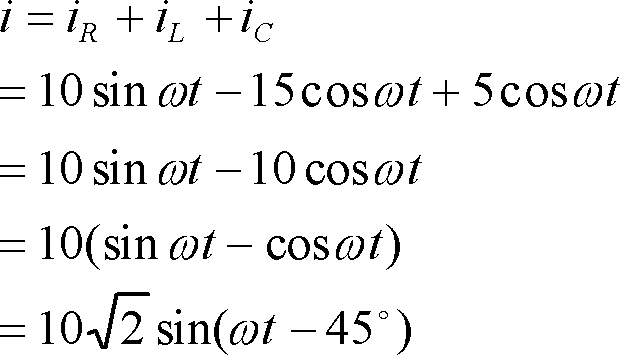
正解は(3)
(補足)
上式の変形は
![]()
![]() を応用している。
を応用している。
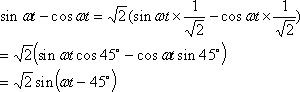
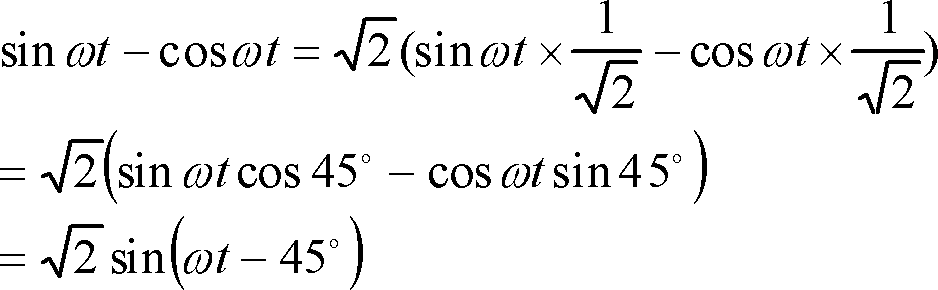
1行目の式の変形によって、正弦の加法定理が利用でき、位相の遅れが読み取れる式が得られた。