まず、交流ブリッジが平衡した条件のもとにおいて

①　各辺のインピーダンスを複素数で表わす。

②　対辺同士の積を等しいとおき、両辺が の形になるようにする。

③　両辺の実数部、虚数部同士が等しいとおく、あるいは等式成立の条件により、測定する未知数を導く。

　例題でこの手順を示してみよう。

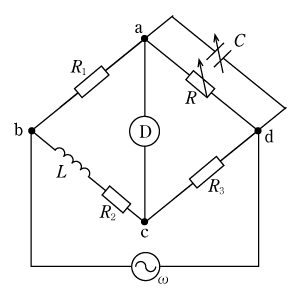
　[例題1]1図のようなマクスウェルの交流ブリッジにおいて、可変コンデンサCならびに可変抵抗Rを測定しようとしたところ、各素子が以下の値のとき、このブリッジは平衡状態になった。CとRの値はそれぞれいくらか。

　　　　R₁=15Ω　R₂=300Ω　R₃=120Ω　L=45μH

■第1図■

　[解答]ab間のインピーダンスを 同様にbc間、dc間、ad間のインピーダンスをそれぞれ とすると

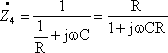
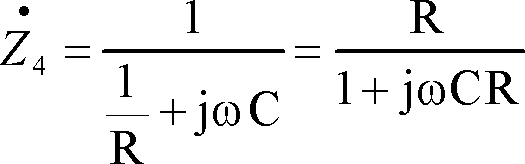
　ブリッジが平衡するための条件は　 　であるから

　右辺の分母を払うと

　よって

　ここで、両辺で実数どうし、虚数どうしは等しいので

　　　　　　 より　　　R=6Ω

　よってC=0.025μF

　[解説]　交流ブリッジの平衡条件が成立した時の解法は、上に述べた①、②、③の順序を正確に実行することによって、解答に到達することができる。

　しかし、実数部と虚数部を含んだ式を導く過程では、数学的処理が重要になる。

　①、②ができても、③の段階で数学的処理にとまどうと堂々巡りしてしまうことがある。時間的な制約のある電験問題などでは、特に数式処理に習塾しておいてほしい。

　このような事例を過去の電験問題から拾ってみることにする。

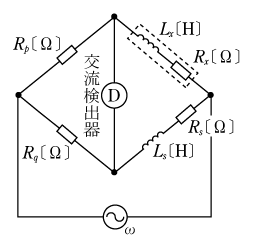
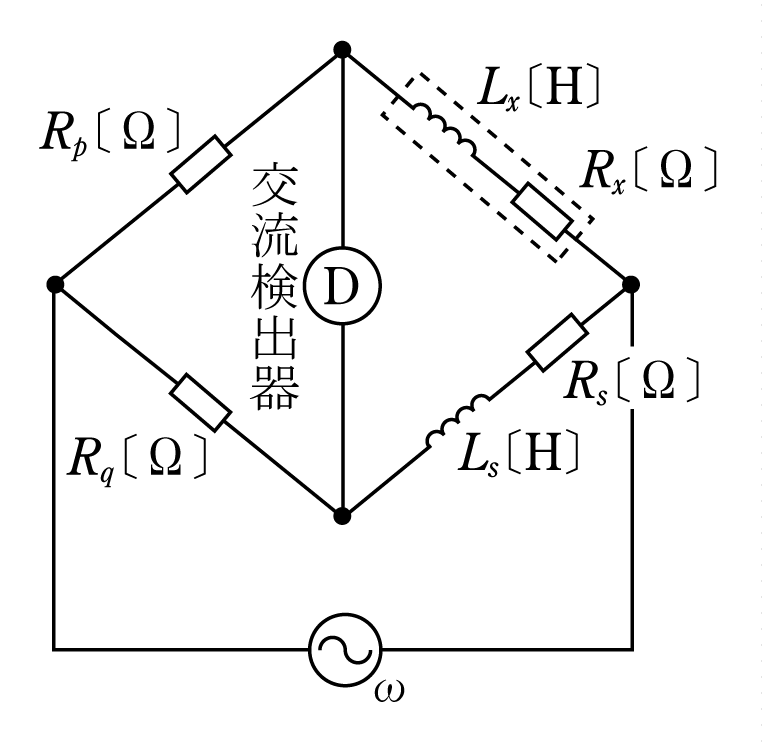
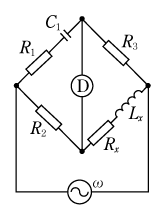
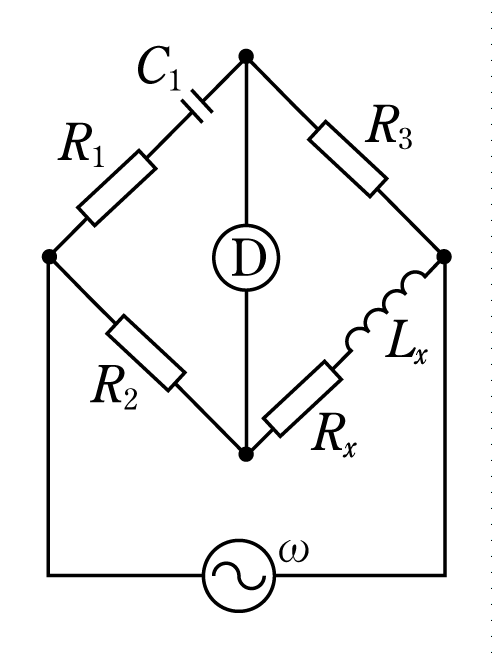
　[例題2]2図は破線で囲んだ未知のコイルのインダクタンスL_x[H]と抵抗　R_x[Ω]を測定するために使用する交流ブリッジの等価回路である。このブリッジが平衡した場合のインダクタンスL_x[H]と抵抗R_x[Ω]の値として、正しいものを組み合わせたのは次のうちのどれか。

　ただし、交流ブリッジが平衡したときの抵抗器の値はR_p[Ω]、R_q[Ω]、標準コイルのインダクタンスと抵抗の値はそれぞれL_s[H]、 R_s[Ω]とする。

■第2図■

　（1） 　　 　　（2） 　　

　（3） 　　 　　（4） 　　

　（5） 　　

　[解答]交流ブリッジの平衡条件は、対辺のインピーダンスの積が等しいから

　2図の回路にこの条件をあてはめると

　したがって　　

　等式が成立するためには

　　　　 　　　したがって　

　また　 　　したがって　 　でなければならない。

　正解は（4）となる。

　この例題では等式の展開が容易であったが、次の例題ではやや複雑になるので上手に展開して解答を導いてほしい。

　[例題3]3図の交流ブリッジが平衡した場合、Cおよびrの値はそれぞれいくらか。正しい値を組み合わせたものを次のうちから選べ。

■第3図■

　（1） 　　 　　　（2） 　　

　（3） 　　 　　　（4） 　　

　（5） 　　

　[解答]当然のことながら、交流ブリッジのそれぞれの辺のインピーダンスを求め、対辺の積を等しいとおくと

　等式　 　が成立する。

　（注意）ここでこの式を展開するため括弧をはずして計算しようとすると、 が分数の分母に表れたりして処理が困難になる。この場合、右辺の分母　（ ）を両辺に掛けると展開しやすくなる。

　以下　　

　　　　　この等式において、実数部どうし、虚数部どうしが等しいから

　　　　　　　　 　　よって　

　　　　　　　 　　　よって　 　

　正解は（2）となる

　実力試しとして、ブリッジの平衡条件式を立てたあとの展開式を正しく導けるかどうか、もう1題。例題をあげますので試してごらんなさい。

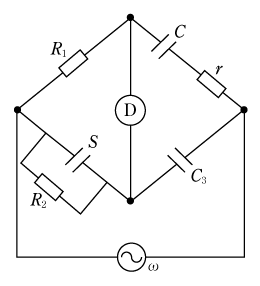
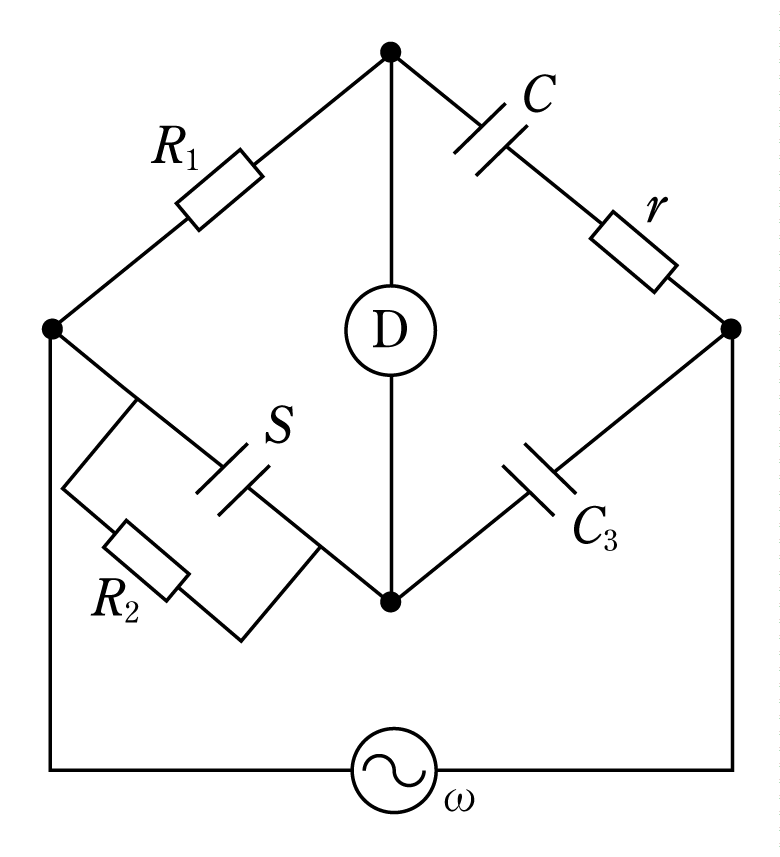
　[例題4]4図の交流ブリッジ回路において、コイルのインダクタンスL_xと抵抗R_xを測定したい。可変抵抗R₁、R₂を調整して平衡を得たときL_x、R_xはどのような計算式でその値を求めることができるか。

■第4図■

　[解答]　4図において、ブリッジが平衡したとき次の等式がなりたつ。

　上式の両辺を で割ると　

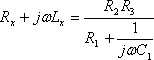
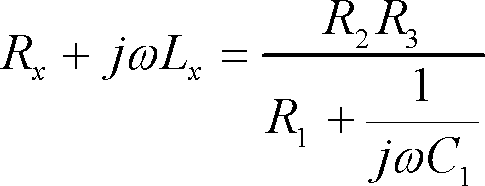　 　ここで右辺を展開すると　 　

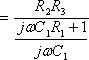
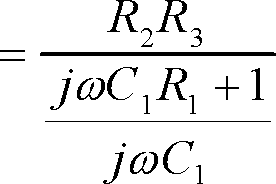
　この右辺をまとめると結局

　 　となり、実数どうし、虚数どうしは等しいので