(ア) 定電圧源
第1図に電圧源の回路を示します。この回路において、出力端子電圧
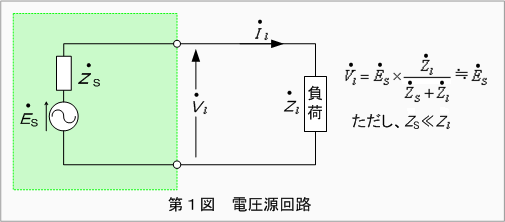
実際の回路では内部インピーダンスが存在していますから、このような理想的な定電圧源とはなり得ませんが、近似的に Zs
≪ Zl の範囲においては、ほぼ定電圧源として扱うことができます。定電圧源の例としましては、改めて列記するまでもありませんが、一般の商用周波電源がこれに該当するわけです。
![]()
(イ) 定電流源
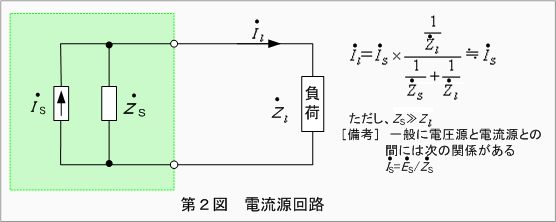
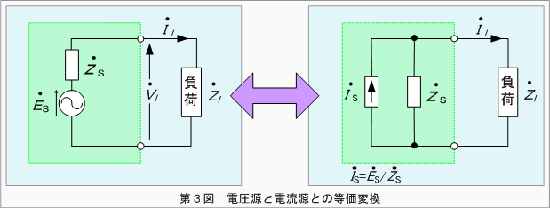
二つの電圧源を並列接続にして負荷に供給する回路があるようなとき、これを電流源回路に変換して分担電流を求める計算例を次に示します。なお本講では、計算を容易にするため直流回路を例に説明します。
第4図に示すような二つの電圧源(電池)Ea =5〔v〕、 Eb =6〔v〕、内部抵抗Ra=0.2〔Ω〕、Rb=0.25〔Ω〕を並列接続にして、これに抵抗Rl=1〔Ω〕を接続した直流回路があります。
この回路を二つの電流源による等価回路に変換し、電圧源Ea 、Eb〔v〕
に流れる電流I1、I2〔A〕及びIl〔A〕
を求めます。
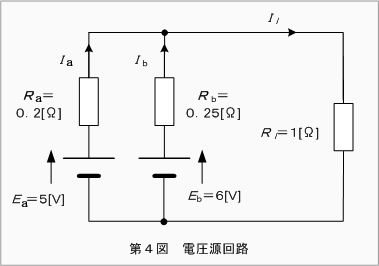
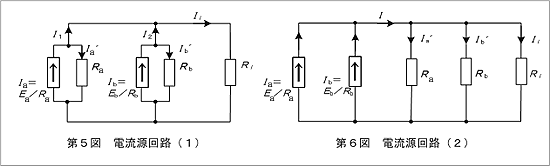
まず、第4図の電圧源回路を第3図にならって電流源回路に等価変換すると第5図のようになります。これをさらに書き換えると第6図となります。
![]()
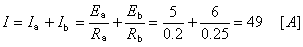
第6図のような並列回路の各分路の電流は、コンダクタンス(抵抗の逆数)に比例配分しますので、負荷電流Il
を求めますと次のようになります。 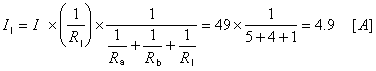
同様にして、Ia´、Ib´を求めますと次のようになります。
Ia´=24.5 [A]
Ib´=19.6 [A]
第5図に戻って、各電圧源(電池)の分担電流I1 、I2を求めると次のようになります。
I1=Ia −Ia´=25−24.5=0.5〔A〕
I2=Ib −Ib´=24−19.6=4.4〔A〕
このようにして、電圧源を電流源に変換しますと並列回路の電流の計算がキルヒホッフの法則を使わずに解くことができとても便利です。
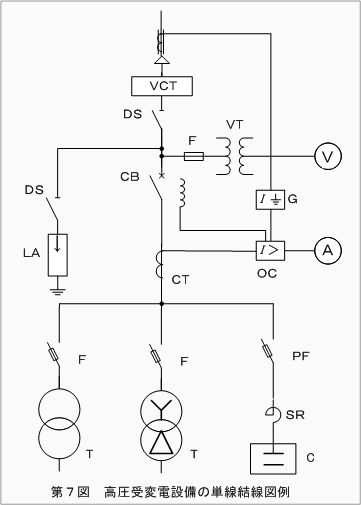
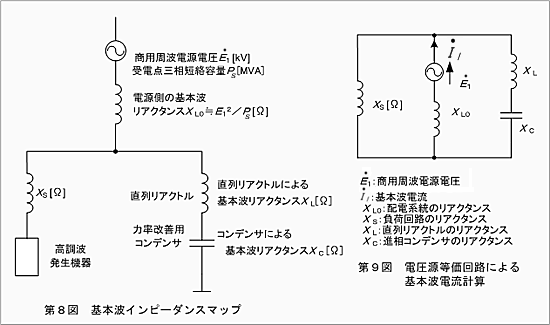
また、第5次高調波電圧ひずみ率が数〔%〕程度含まれている配電系統では、高圧進相コンデンサ(直列リアクトルを含む)を接続したときの当該進相コンデンサ設備への高調波電流の計算は、基本波の場合と同様に電圧源回路として扱われます。
一方、高調波発生機器からの高調波電流流出量の計算では、商用電源側から見て高調波電源は、負荷側にあることになりますので高調波発生機器のインピーダンスは、配電系統の合成インピーダンスと進相コンデンサ設備のインピーダンスとの合成値に比べて、十分大きいものとみなすことができます。
したがって、高調波発生機器による高調波電流の計算は、電流源回路として扱われます。高調波回路のインピーダンスマップは第10図となり、その等価回路は第11図のようになります。
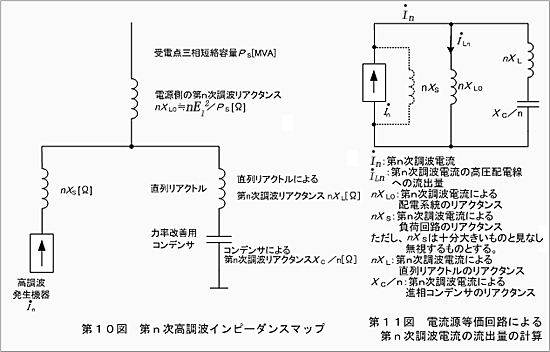
「高圧又は特別高圧で受電する需要家の高調波抑制対策ガイドライン」(資源エネルギー庁公益事業部長通達平成6年10月3日)で求めている第n次高調波電流の配電線への流出量
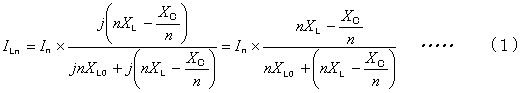
実際に第5次高調波,第7次高調波電流の流出量は、それぞれ(1)式において、n=5又は7として計算すればよいことになります。したがって(1)式、は第n次高調波電流の配電線への流出量ILn を求める際の基本式といえます。
近時、制御回路等の弱電流回路計算や高調波電流の流出量計算に見られるように、強電関係の技術者にも電流源に遭遇する機会が多くなってくるものと思われます。


