最近、電気工学関係ではべクトルのことをフェーザとも称しているが、従来のべクトルとどう違うのか疑問にもつ方も少なくないと思われる。この問題を考える前に、まずベクトルについての基本的なことについて整理する。
べクトルとは英語でvectorと書き、べクトル、方向量〔大きさと方向をもつ量〕等と訳されている。例えば、力学では速度 ![]()
![]() 、加速度
、加速度 ![]()
![]() 、力
、力 ![]()
![]() 、運動量
、運動量 ![]()
![]() 、電気磁気学・電気回路理論では電界
、電気磁気学・電気回路理論では電界 ![]()
![]() 、磁界
、磁界 ![]()
![]() 、電流
、電流 ![]()
![]() 、起電力
、起電力 ![]()
![]() 、起磁力
、起磁力 ![]()
![]() 等をべクトル量(vector quantity)といっている。これらのうち正弦波交流(電圧
等をべクトル量(vector quantity)といっている。これらのうち正弦波交流(電圧 ![]()
![]() 、電流
、電流 ![]()
![]() )のように回転べクトルであって、大きさと位相という二つの量によって定まるものを近頃フェーザ(phasor)と呼び、複素数を使って表示している。また、長さ
)のように回転べクトルであって、大きさと位相という二つの量によって定まるものを近頃フェーザ(phasor)と呼び、複素数を使って表示している。また、長さ
![]()
![]() 、面積
、面積 ![]()
![]() 、体積
、体積 ![]()
![]() 、質量
、質量 ![]()
![]() 、時間
、時間 ![]()
![]() 、仕事量
、仕事量 ![]()
![]() (エネルギー
(エネルギー ![]()
![]() )、仕事率
)、仕事率 ![]()
![]() 等のように単に大きさだけをもつ量を総称してスカラー量(scalar quantity)といっている。
等のように単に大きさだけをもつ量を総称してスカラー量(scalar quantity)といっている。
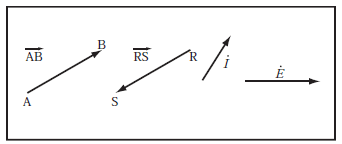
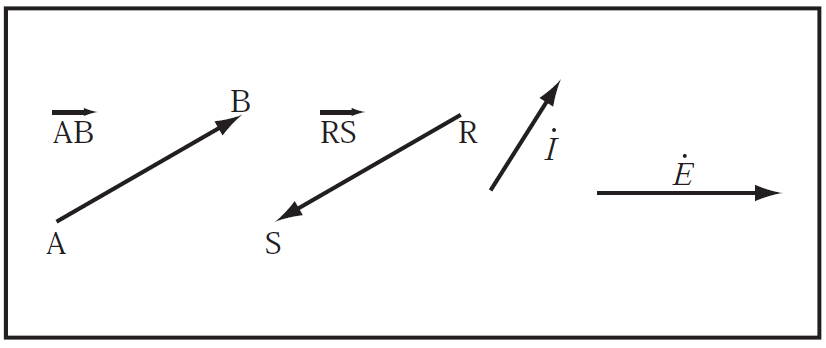
べクトルをべクトル図によって表すときには、矢印を付けた線分で表す。線分をべクトルの方向に合わせ、その大きさに比例する長さにして直線を引き、べクトルの方向は矢印で示すようにする。その位置はどこでもよく、大きさと方向を明示すればよいことになる。
例えば、第1図に示すように![]()
![]() 、
、![]()
![]() 、
、 ![]()
![]() 、
、 ![]()
![]() 等として表される。
等として表される。
ABの場合、Aをベクトルの起点、Bをベクトルの終点といっている。二つのベクトルが等しいということは、二つのベクトル大きさと方向とが等しいということである。
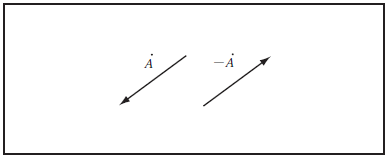
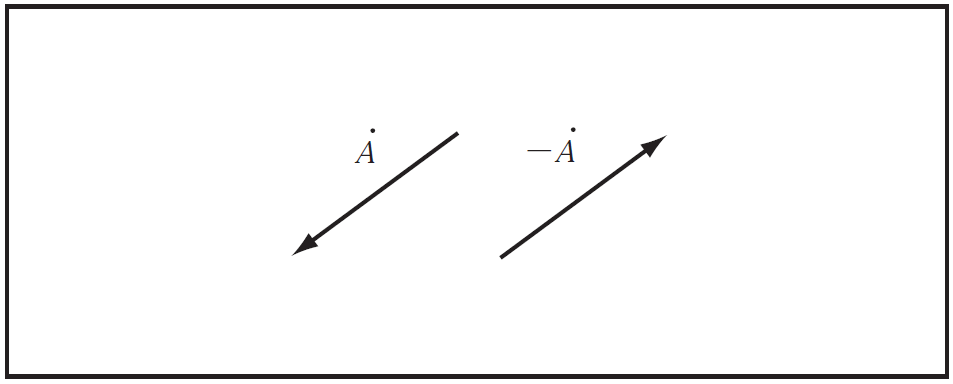
即ち、二つのベクトル線分の長さが等しく、かつ方向が等しい(線分が平行になる)ということである。従って、ベクトルは任意の位置に平行移動して描いてもよく、また第2図に示すようにベクトル
![]()
![]() と
と![]()
![]() とは大きさが等しく、方向が反対(位相が180°異にする)のベクトルを表すものといえる。
とは大きさが等しく、方向が反対(位相が180°異にする)のベクトルを表すものといえる。
次にベクトル計算例として、よく経験するケース2題を紹介する。
[1] 力学関係のベクトル計算例
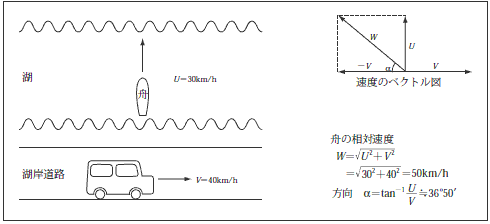
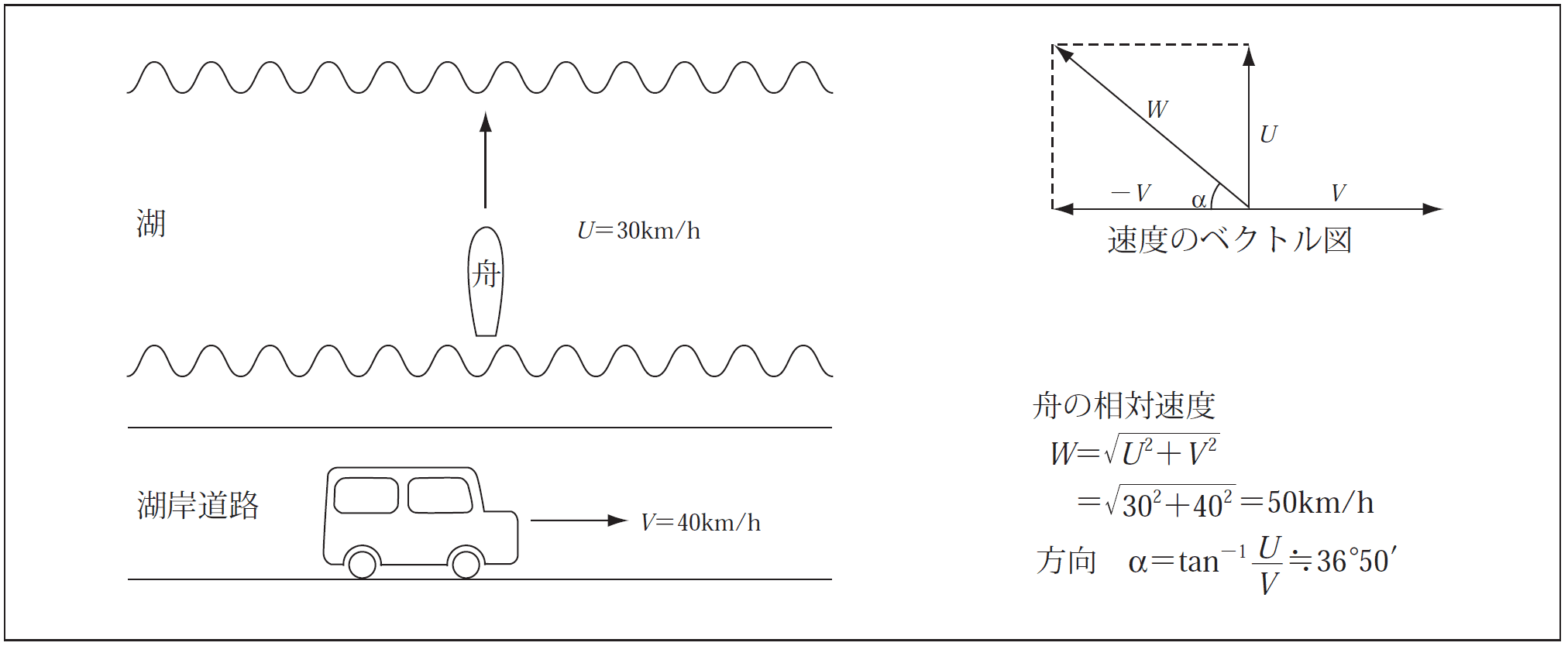
〔例題1〕 湖岸の道路を速度40km/h自動車に乗っている人が、対岸に直角に向かう速度30km/h渡し舟を見る時、車内からどのような方向にどのくらいの速度で航行しているように見えるか。
第3図に示すように湖岸を走る自動車の速度を ![]()
![]() =40km/hとし、対岸に直角に航行する舟の速度を
=40km/hとし、対岸に直角に航行する舟の速度を ![]()
![]() =30km/hとすると、自動車に乗っている人は、自分が止まっているものとして相手の舟を眺めることになるので相対速度ということになる。従って、自分を止めるため反対方向に
=30km/hとすると、自動車に乗っている人は、自分が止まっているものとして相手の舟を眺めることになるので相対速度ということになる。従って、自分を止めるため反対方向に
![]()
![]() 〔km/h〕の速度を両者に対し加ると、舟は第3図のベクトル図から
〔km/h〕の速度を両者に対し加ると、舟は第3図のベクトル図から ![]()
![]() の速度で車の走行方向とは反対方向に、道路に対し約36°50′の角度をなして航行しているように見えることになる。
の速度で車の走行方向とは反対方向に、道路に対し約36°50′の角度をなして航行しているように見えることになる。
[2] 交流回路関係のベクトル(フェーザ)計算例
正弦波交流を波形で表す方法は視覚的には分かり易いと思うが、電圧や電流等を計算するには波形をグラフに書かなければならず、実用的ではない。
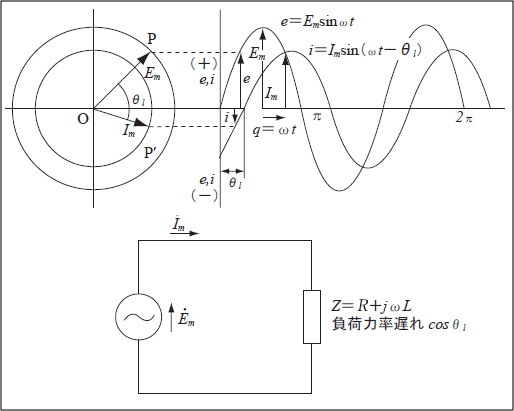
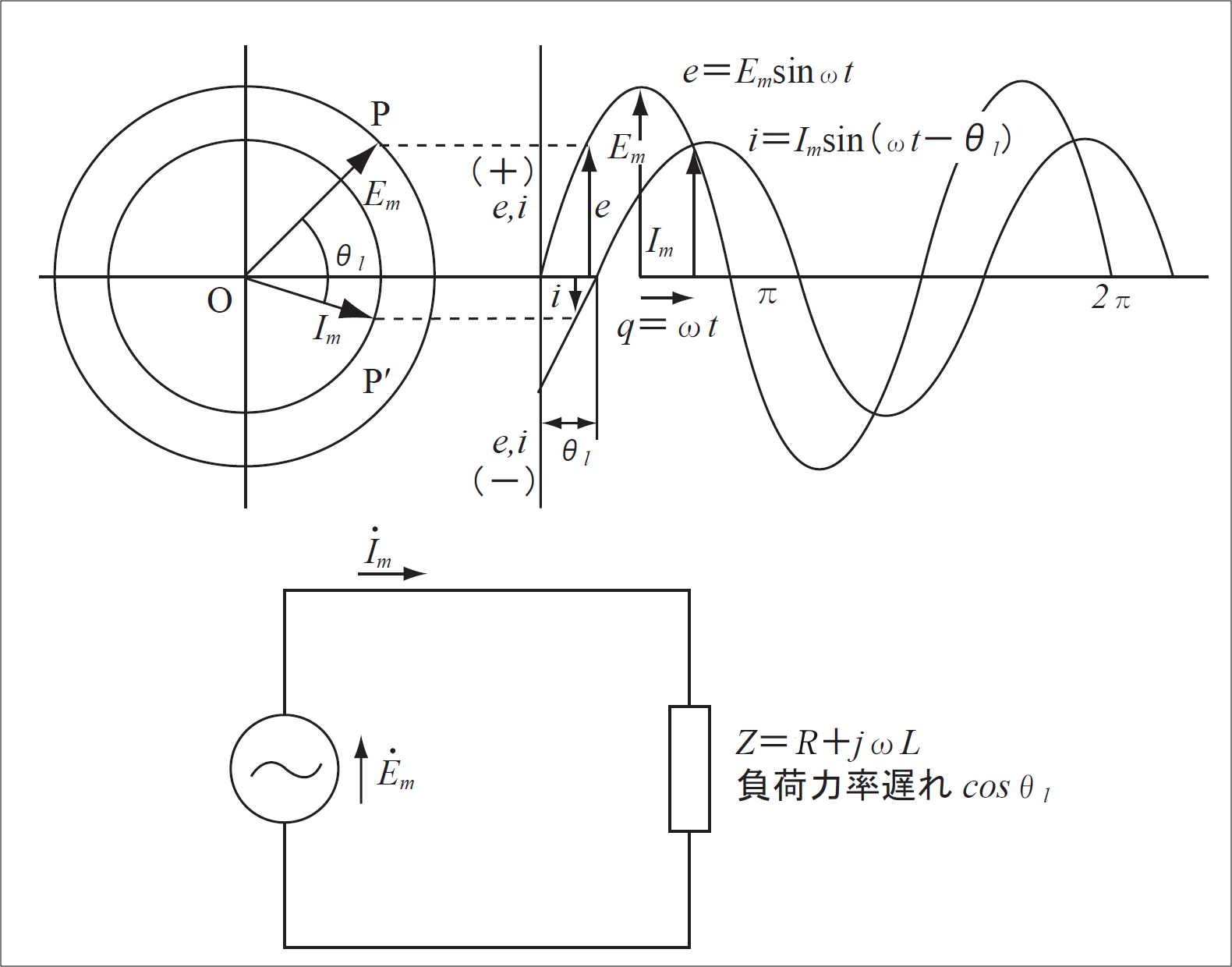
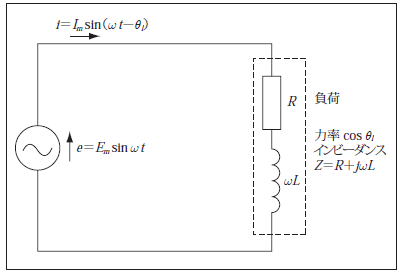
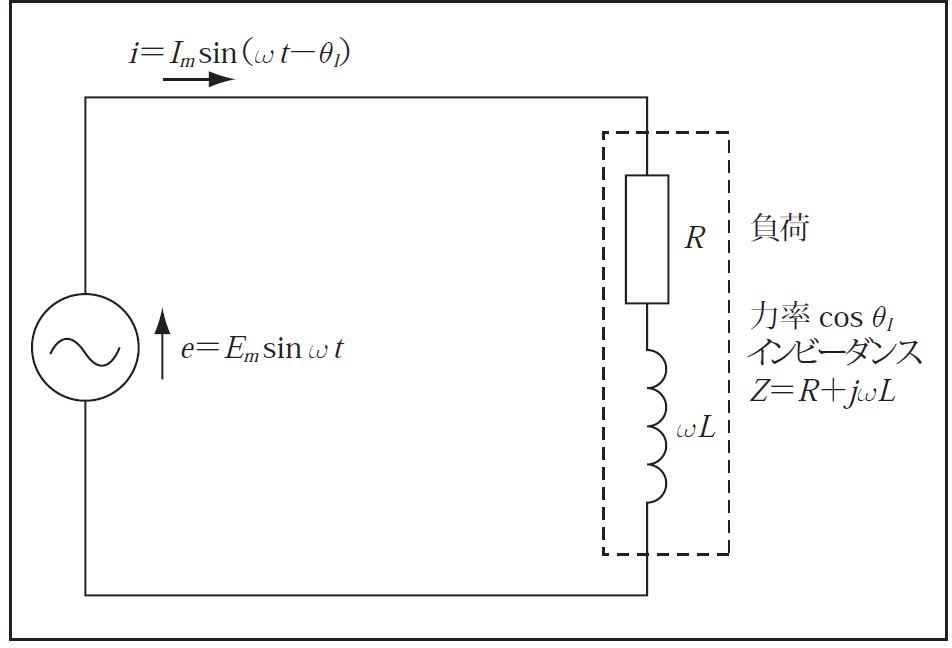
通常使用する正弦波交流計算は、瞬時値や最大値ではなく実効値を使用している。例えば、交流発電機の誘導起電力 ![]()
![]() を、抵抗
を、抵抗 ![]()
![]() 、リアクタンス
、リアクタンス ![]()
![]() 、負荷力率 遅れ
、負荷力率 遅れ ![]()
![]() の直列回路に印加すると、
の直列回路に印加すると、 ![]()
![]() の負荷電流が流れる。これを回転ベクトルで表すと
の負荷電流が流れる。これを回転ベクトルで表すと ![]()
![]() と
と ![]()
![]() との関係及びその波形は第4図のようになる。第4図で
との関係及びその波形は第4図のようになる。第4図で ![]()
![]() は
は ![]()
![]() から生ずるものであるから
から生ずるものであるから ![]()
![]() と
と ![]()
![]() の回転角速度は
の回転角速度は ![]()
![]() で一定である。よって
で一定である。よって ![]()
![]() と
と ![]()
![]() とは常に
とは常に ![]()
![]() だけ「ずれ」(相差角)ながら反時計式に回転する。
だけ「ずれ」(相差角)ながら反時計式に回転する。
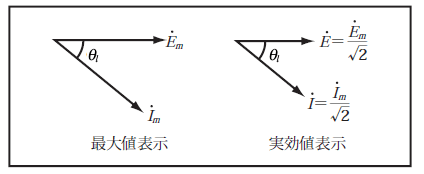
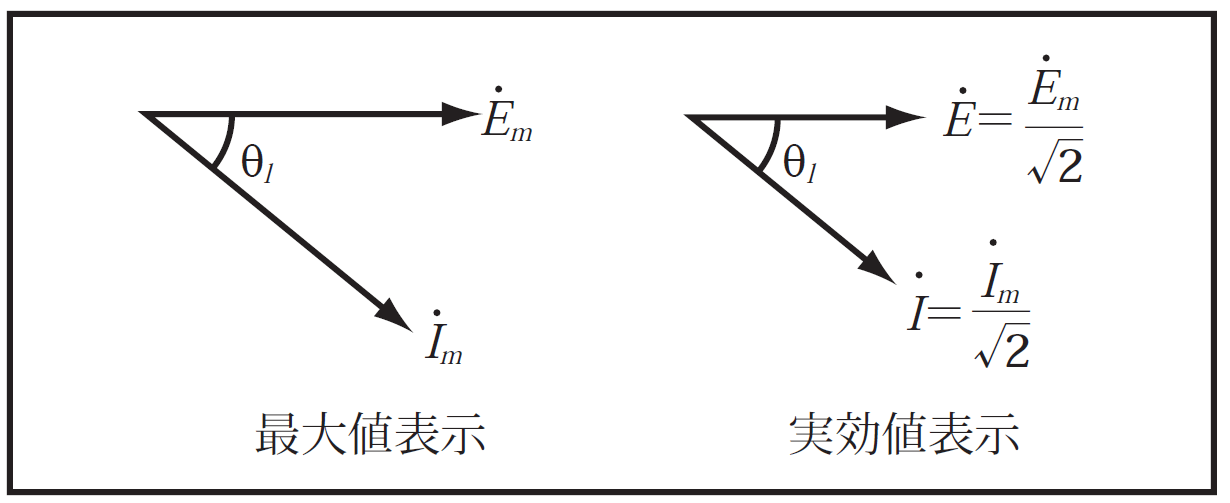
従って、電圧、電流相互の関係を考える際にはこの回転ベクトルを静止ベクトルとし、また大きさについても最大値とせず実効値で扱うようにしている。すなわち、第5図に示すように最大値
![]()
![]() 、
、 ![]()
![]() のそれぞれの
のそれぞれの ![]()
![]() 倍を実効値
倍を実効値 ![]()
![]() 、
、![]()
![]() として、その線の長さが電圧、電流の実効値、矢印がその方向、両ベクトルのなす角度が相差角となる。
として、その線の長さが電圧、電流の実効値、矢印がその方向、両ベクトルのなす角度が相差角となる。
正弦波交流では第4図に示すように原点Oを基点とする1本の基準線とOを中心に回転する動径OPは、大きさと位相との二つの量によって定まる。
位相は、初期位相 ![]()
![]() と角速度
と角速度 ![]()
![]() とによって決定される。一定角速度で回転する場合に、一般に初期位相を与える。このような動径OP(ベクトル)をフェーザといい、複素平面に描いたものをフェーザ図といっている。
とによって決定される。一定角速度で回転する場合に、一般に初期位相を与える。このような動径OP(ベクトル)をフェーザといい、複素平面に描いたものをフェーザ図といっている。
即ち、交流回路のベクトル図は、一般にある基準ベクトルを横軸にして実効値で描かれ、これを従来ベクトル図といっていたが、近頃一般的な静止ベクトル図に対して区別をしてフェーザ図と称している。
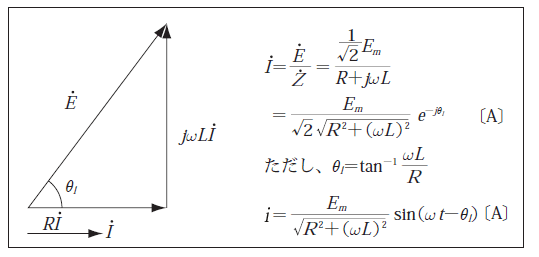
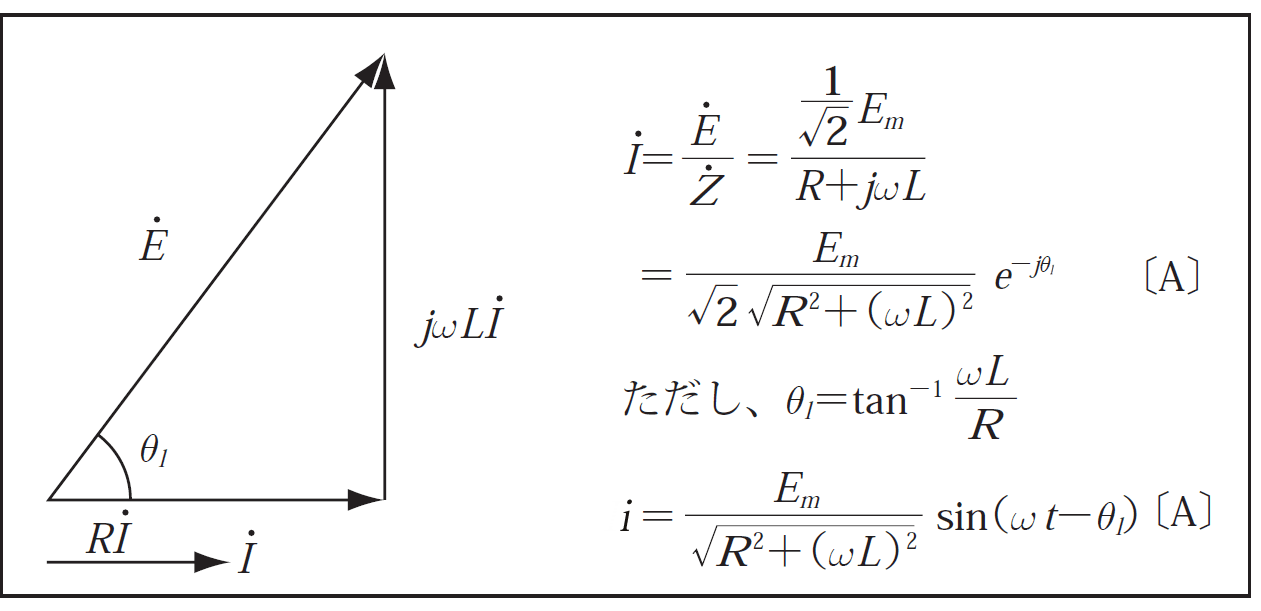
〔例題2〕 第6図に示すような負荷である 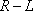
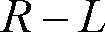 直列回路に、
直列回路に、 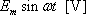
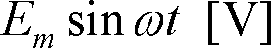 の交流電圧を加えるとどのような負荷電流が流れるか。
の交流電圧を加えるとどのような負荷電流が流れるか。
負荷電流の実効値 ![]()
![]() 、瞬時値
、瞬時値 ![]()
![]() を計算すると第7図に示すようになる。
を計算すると第7図に示すようになる。