では、微分法を用いた計算ではどのように数式(関数)の変化を捉えていくのであろうか。微分に関する基礎的な理解を得たうえで、例題に取り組んでみよう。


電磁気回路においては、磁束や電荷の時間的変化にかかわる現象があり、それを数式化して解く課題が多く、微分はこのような変化をスマートに取り扱う道具である。ここでは、微分に関する基礎事項と、例題による具体的な取り扱いについて解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
※テキスト中の図はクリックすると大きく表示されます
電気工学には電磁誘導に関するファラデーの法則や自己誘導作用、あるいはコンデンサの充電電圧の時間変化など、いろいろな電気現象の変化の様子を数式化して解く課題が多い。このような変化の様子を細かく調べたいときに、微分という手段を使うことによってスマートに答を得られるので、ぜひ微分に親しんでほしい。
では、微分法を用いた計算ではどのように数式(関数)の変化を捉えていくのであろうか。微分に関する基礎的な理解を得たうえで、例題に取り組んでみよう。
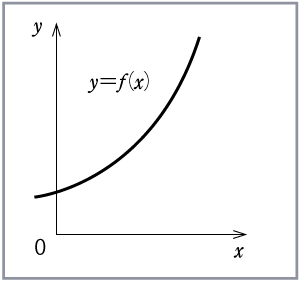
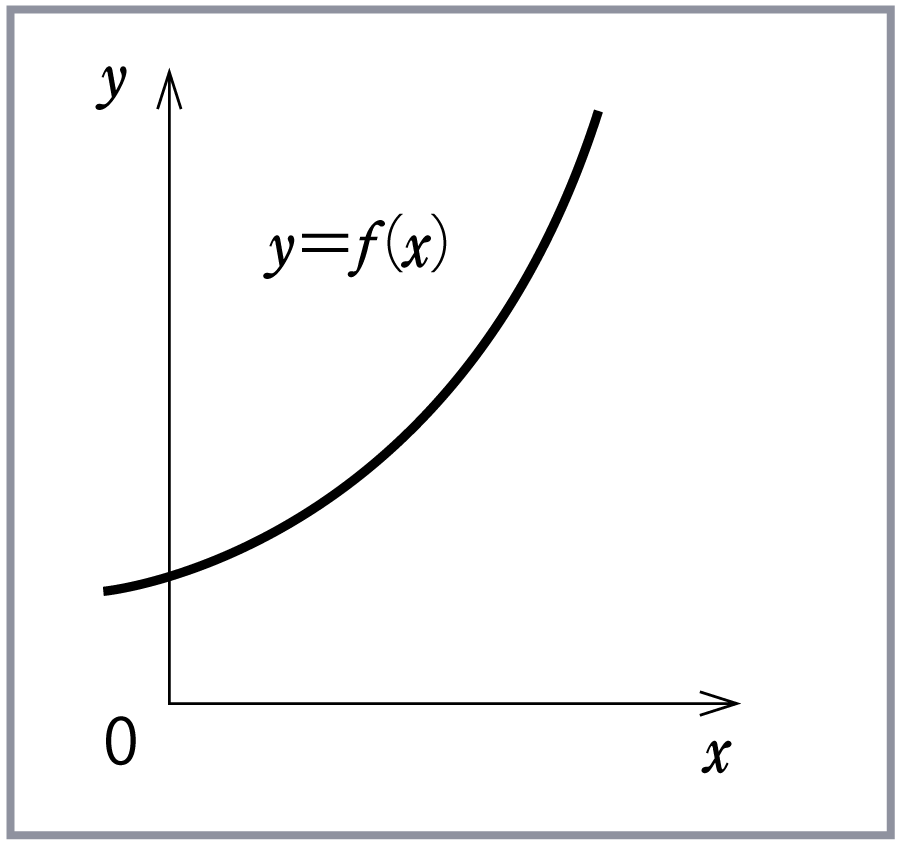
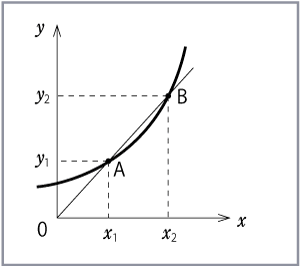
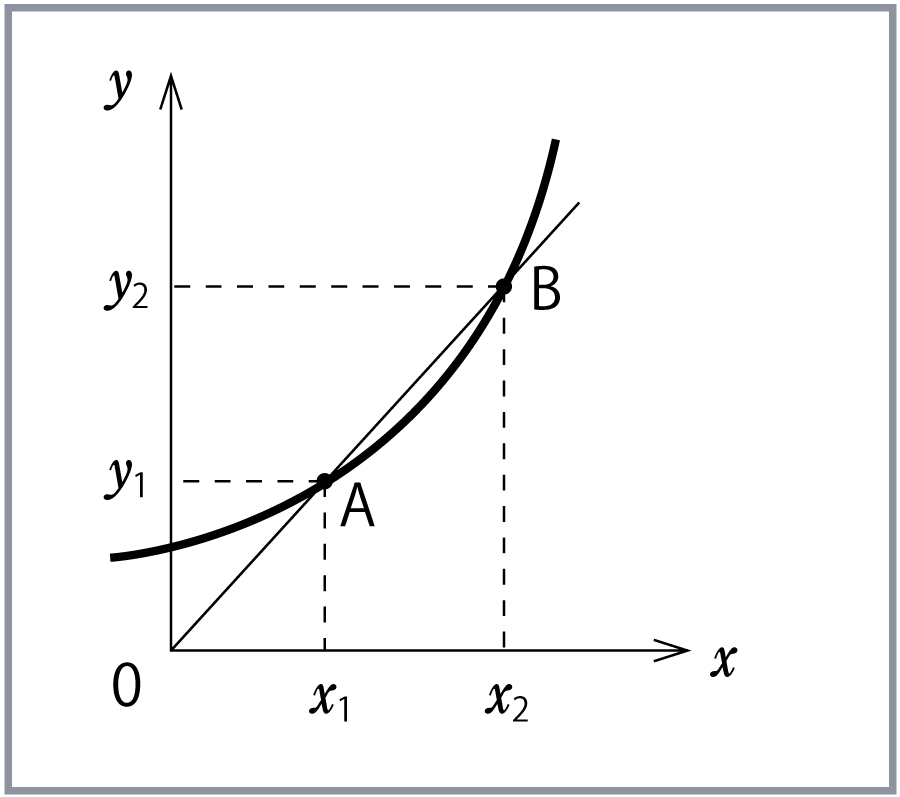
y=f(x)の曲線上の細かい変化の様子を知るには、平均変化率の幅をできるだけ狭めていきたい。Δxを限りなく0近づけることをこのように表現する。
つまり、
さて、関数y=f(x)において xが(x1)から(x1+Δx)までの平均変化率は、
(例題1)
y = f(x) =x2+3x-4 において、xがx1 = -1 からx2 = 2まで変 化するときの平均変化率を求めよ。(解答)
(例題2)
関数 f(x) = x2 - 2x+1 の x = x1 における微分係数を求めよ。(解答)
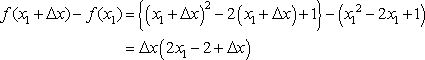
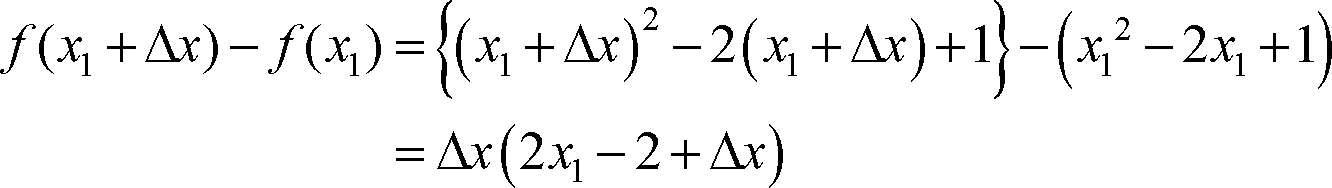
実は、この接線の符号が大きな意味をもっている。それは符号が正であれ ばx1点で曲線は右上がりになっているし、また逆に負であれば曲線は右下が りになっている。微分係数を求める目的は、この曲線の状態を調べるうえで 大切なな役目を果たす。
例えば、電気現象の状態の変化が関数で表された場合に、二つの点の微分係数を求めて、もし正の値から負の値になっていれば、その途中に最大値が存在することが分かる。逆に、負の値から正の値になっていればその途中に 最小値が存在することになる。
f'(x)を求めることが微分するということであるが、f'(x)のほかに y' 、
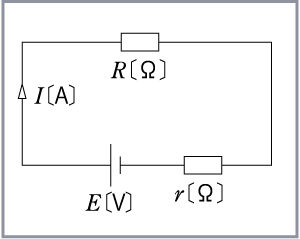
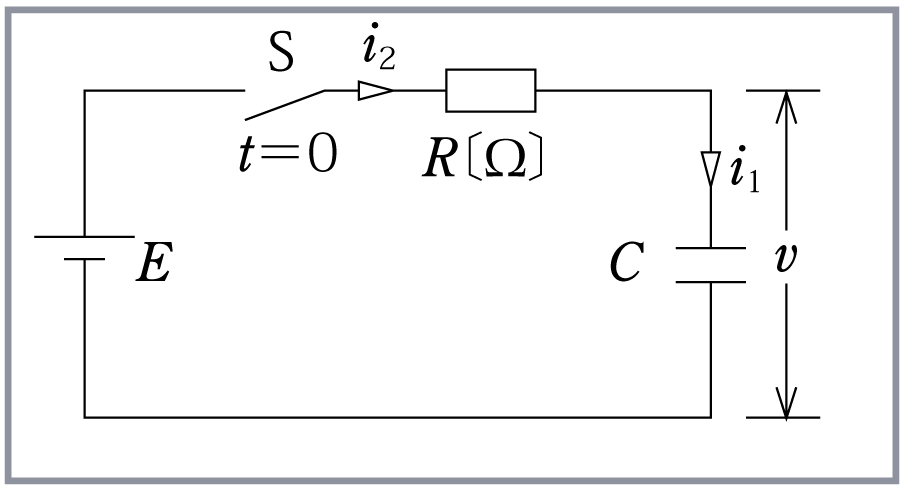
例えば、第3図の回路で抵抗Rに発生する熱量Wは毎秒当たりどうなるだろうか。
抵抗Rに生ずるジュール熱Wは 毎秒W = I2R〔J〕となる。また、この 回路で電流Iは
(例題3)
発生熱量(考え方)
今この式でRを大きくして、R→∞とすると、分母、分子とも∞になって しまうが、ただ分母のほうにR2があるため、分母の大きくなり方が分子を押さえ、W→0になることが想像できる。したがって、Wは大きくならない。また、R→0にすると、分子→0になるから、やはりW=0になる。
以上のことから、R→∞、R→0の途中に最大値のあることが予想される。
この変化の様子を細かく調べるのに、微分を使うと便利である。
(参考)
ここで 関数(解答)
したがって、
(例題4)
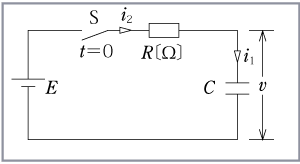
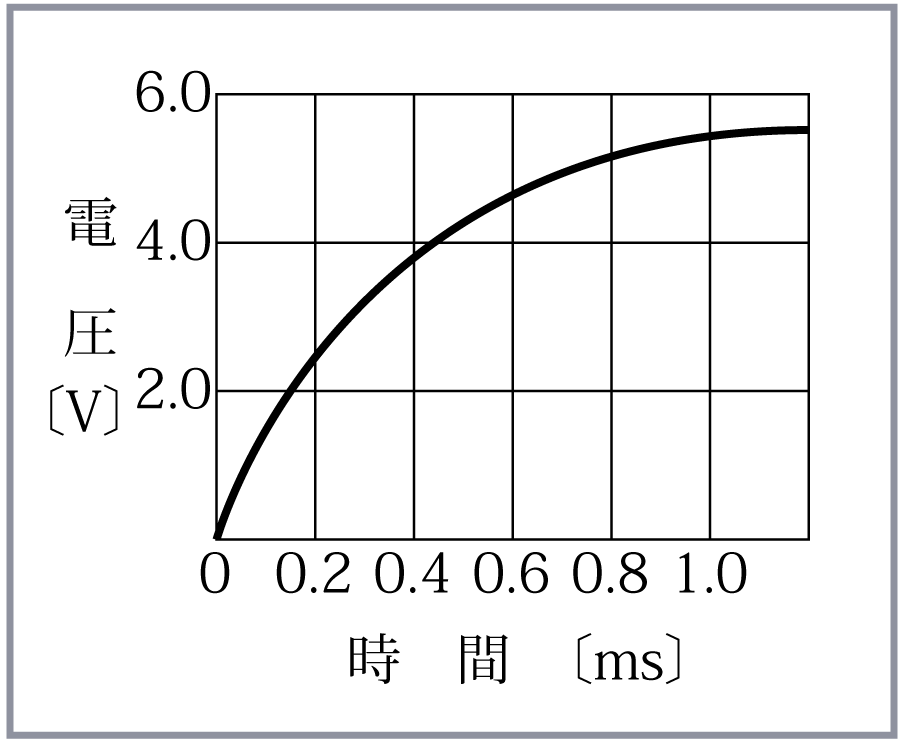
第4図のような抵抗R、コンデンサC、直流電圧E及びスイッチSを直 列に接続した回路で、コンデンサCに加わる電圧vの時間に対する変化が 第5図に示す状態であるとき、次の空欄の下線に入れる正しい文字を、下記文字群から選べ。ただし、はじめ、コンデンサCの電圧v=0であり、時刻t=0でSを 閉じるものとする。
コンデンサに流れ込む電流i1 と電圧上昇率
i2= (い) ( (う) -v)
(文字群)
R 、 1/R 、 C 、 1/C、 E(解説と解答)
この問題はスイッチを閉じてから定常状態に落ち着くまでの時間tの経過 に対するコンデンサの端子電圧vの変化の様子を問題にしている。したがっ て、微分の分野の問題であり、設問は微分方程式を立てる部分があるが、時 間経過の途中の問題といっても、要は瞬間、瞬間を止めて考えればよい。第5図のグラフを0から0.8msまでの時間を一定の幅で、小さく区切って みると、そのつど電圧vの変化が一定でないことが分かる。
したがって、コンデンサの端子電圧vの大きさを示すには、いつの時間帯 での大きさなのかをいう必要が出てくる。このことを
(電荷)Q =(静電容量)C×(電圧)V
したがって、
次にスイッチを閉じて定常状態に至るまで、抵抗Rに加わる電圧は (E - v)〔V〕であるから、流れる電流i2は
このことから
〜終わり〜
■ぜひアンケートにご協力下さい■