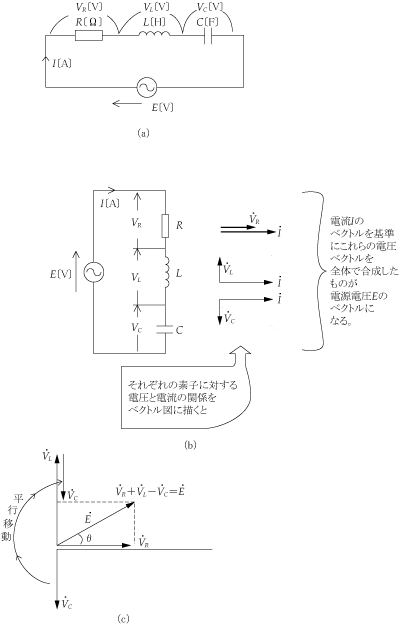
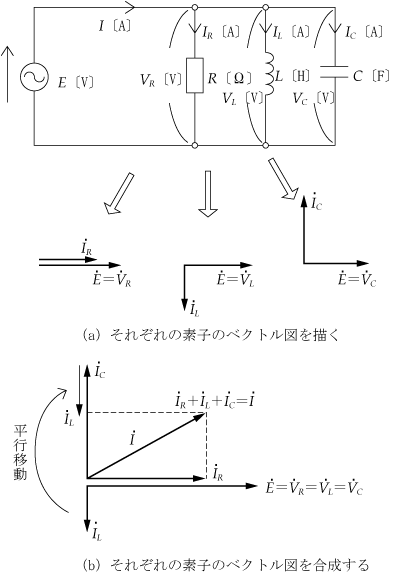
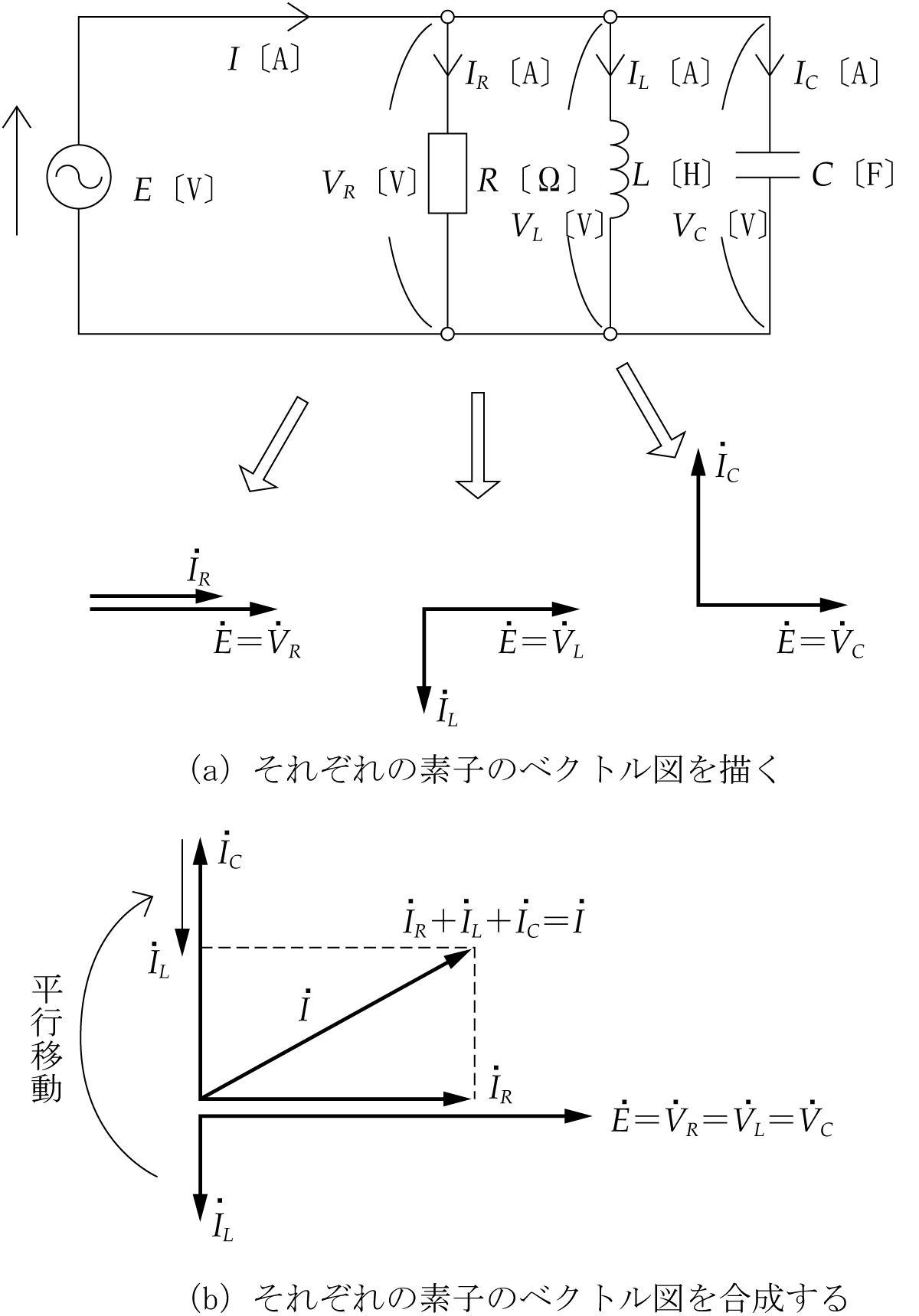
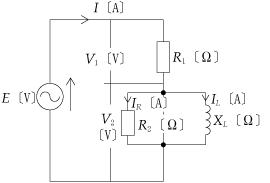
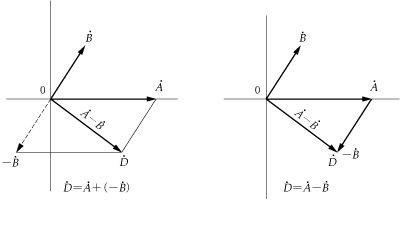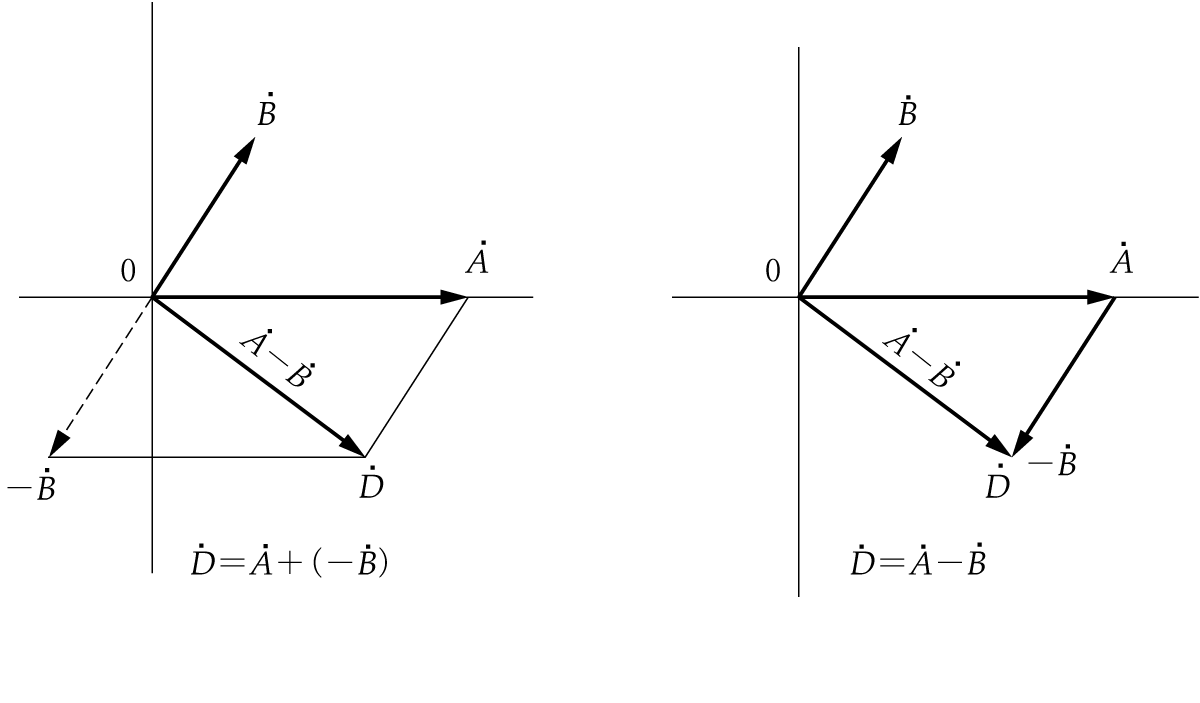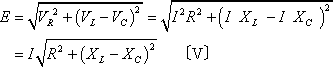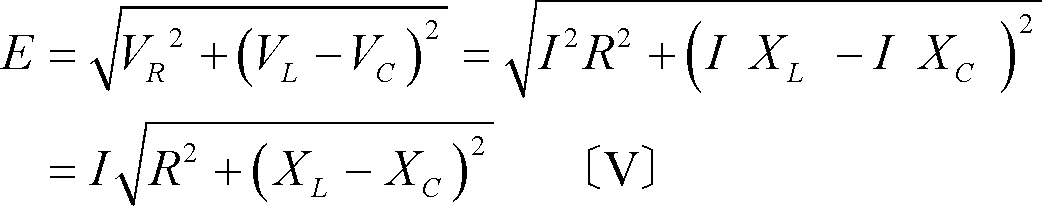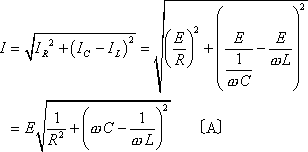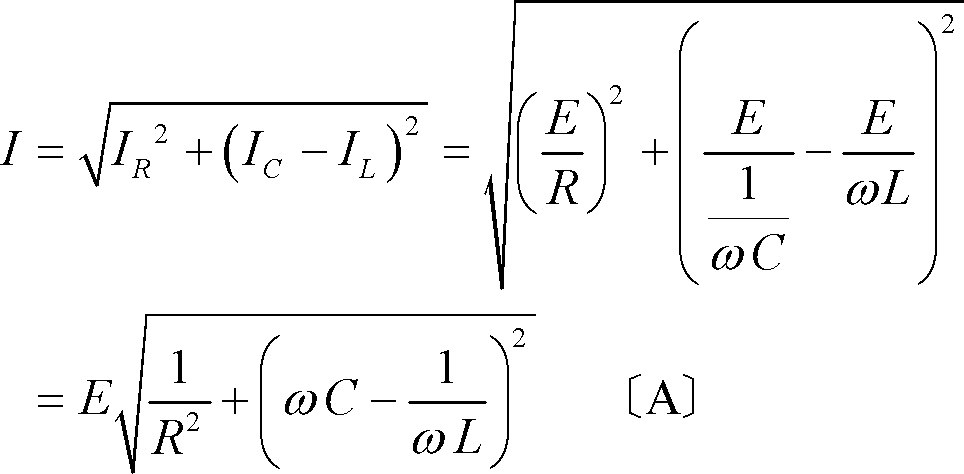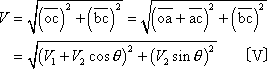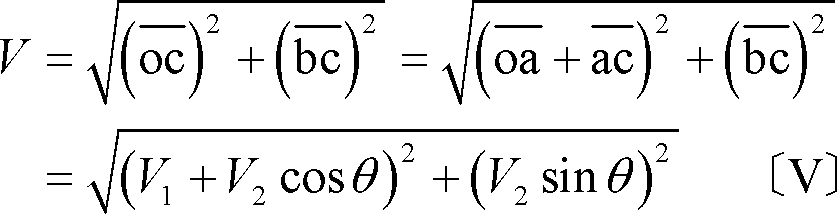正弦波交流回路の電圧、電流は、本来、瞬時値計算しなければならないが、定常状態に限って言えば、系統各部の電圧、電流の大きさの比、位相差は一定である。この性質を利用することにより、正弦波交流回路の瞬時値をベクトルに置き換えれば計算が簡単になる。ここでは、ベクトルの合成と交流電気回路計算への適用例を解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your
Flash plugin.
※テキスト中の図はクリックすると大きく表示されます
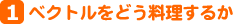
(1) ベクトルは絶対値(矢の長さ)と偏角(傾き)で表す
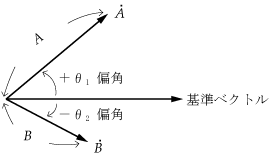
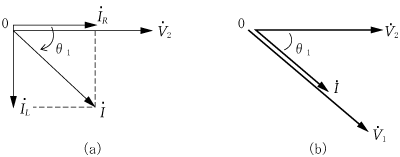
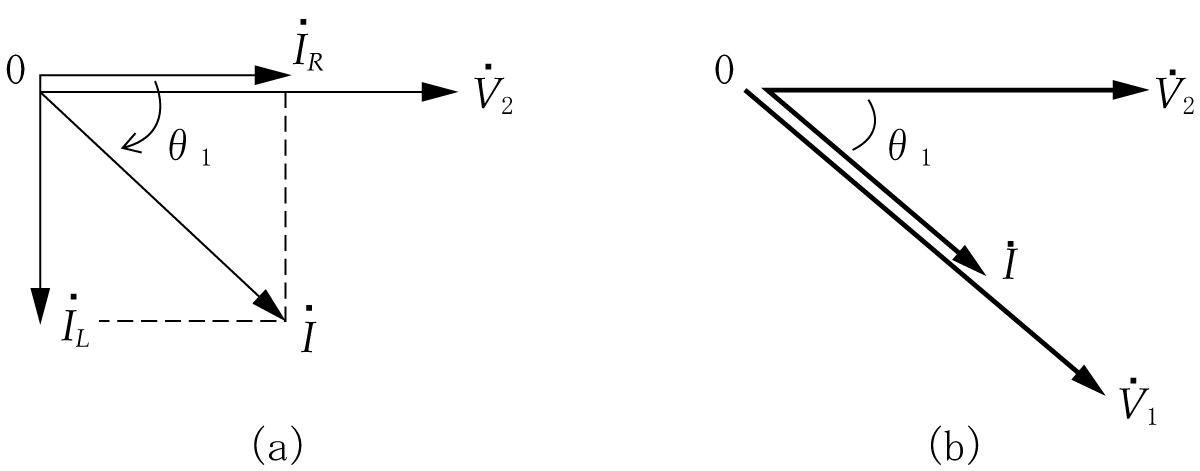
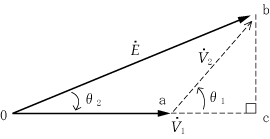
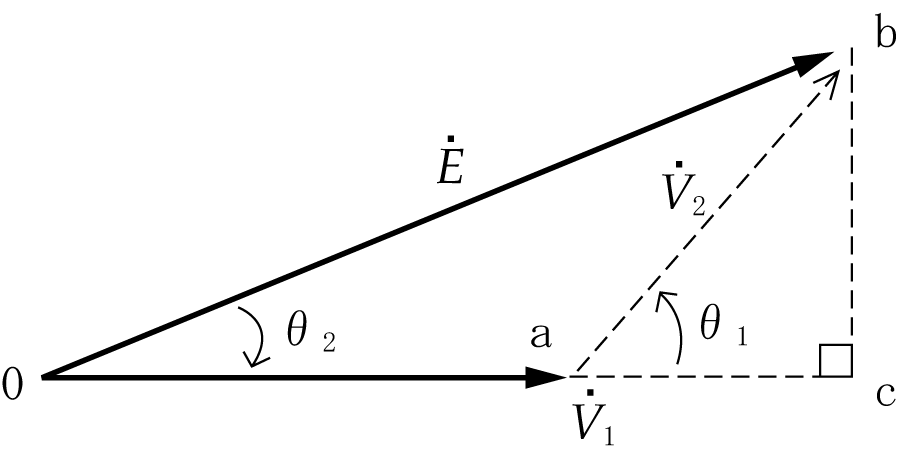
方向と大きさをもつベクトルは矢印で表現されるが、ベクトルの方向は空間的に考えると無数にあることになる。そこでそのベクトルを含む平面上(例えば、紙面に書かれるベクトルは同一平面上にあるといえる)で扱えば、ベクトルの位置や向きをはっきりさせることができる。したがって、第1図のように基準ベクトルに対して偏角によって、ベクトルの方向を表している。
この場合、
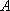
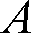
の文字の上に「・」が付いているが、これはドット
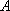
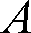
と読み、ベクトル記号を示し、その大きさは(絶対値)は
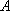
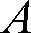
と書く。また、偏角は基準ベクトルから反時計方向に測った角度を正(+)とし、時計方向に測った角度を負(−)として扱うことにしている。
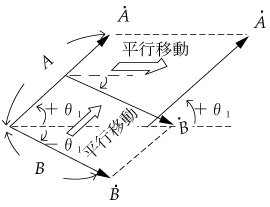
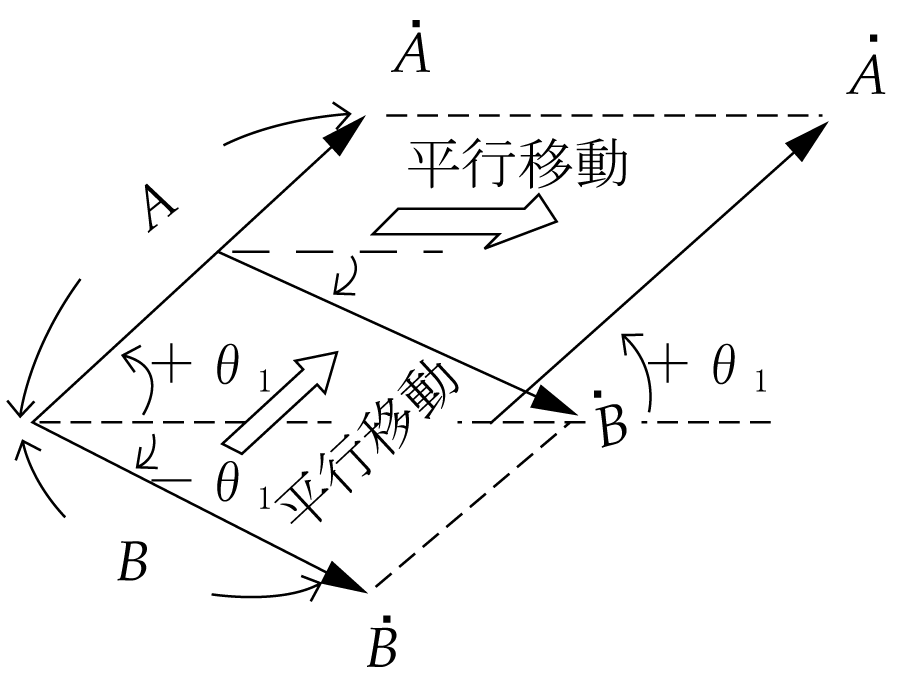
(2) ベクトルは平行移動できる
第2図のように同一平面上にある、いろいろな向きのベクトルは平行移動できる。
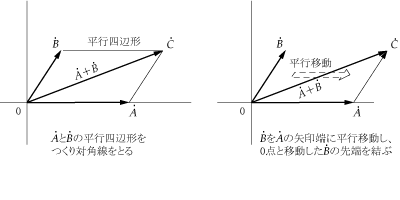
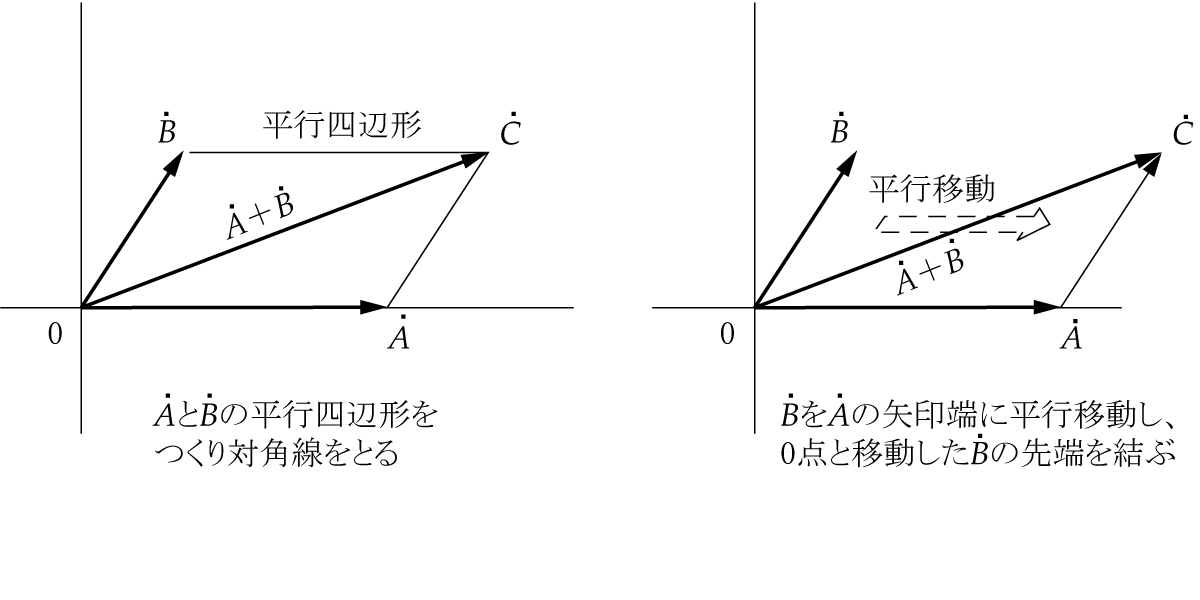
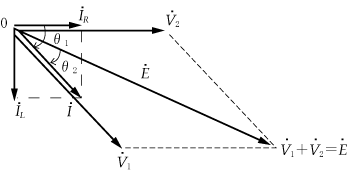
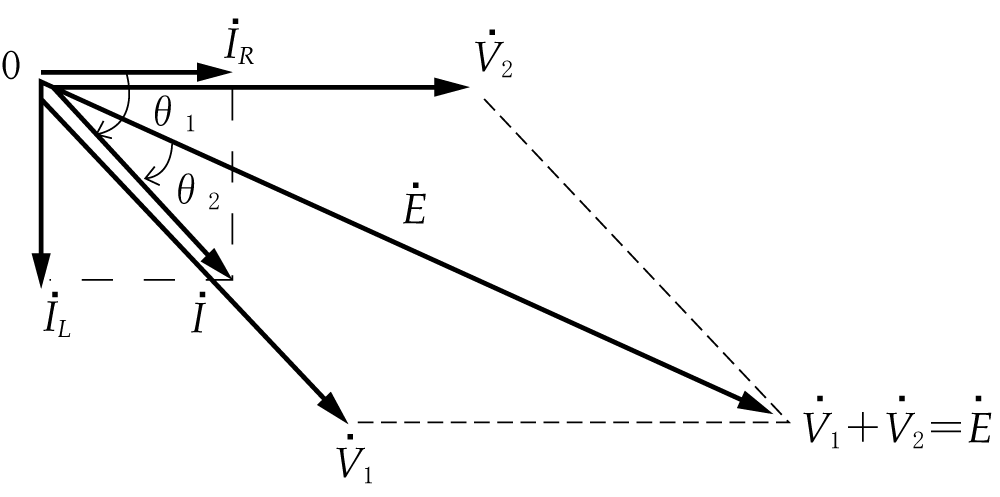
(3) ベクトルの和も差も対角線がねらいどころ
ベクトルの和を求め方(第3図)
ベクトルの差の求め方(第4図)