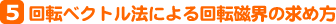誘導機や同機機など回転電気機械は、回転磁界を利用し誘導起電力やトルクを発生させる。ここでは、二相または三相交流電流を固定子や回転子の巻線、導体に流すことにより回転磁界を発生させる原理、回転速度について解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
※テキスト中の図はクリックすると大きく表示されます
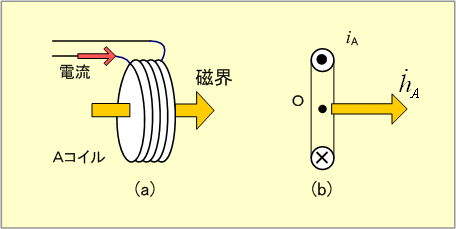
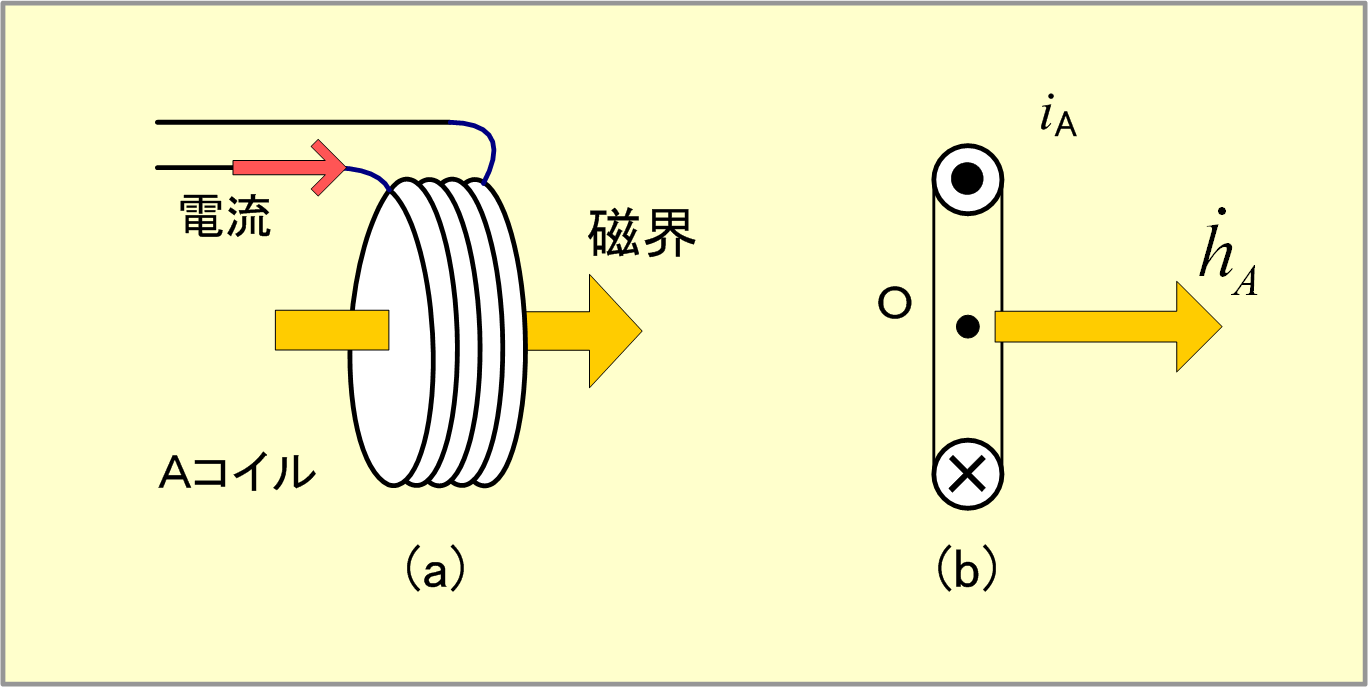
第1図(a)のようなコイルAに電流を流してコイル内に磁界をつくることを考えてみる。第1図(b)に示す断面図でコイルの中心Oにできる磁界は電気理論で学んだように、コイルに流れる電流に比例する。第1図(b)に示す方向を電流の正方向とすれば、この電流iAによってできる磁界
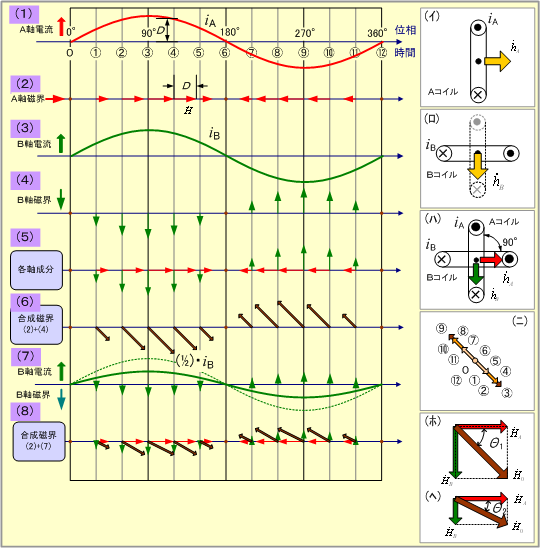
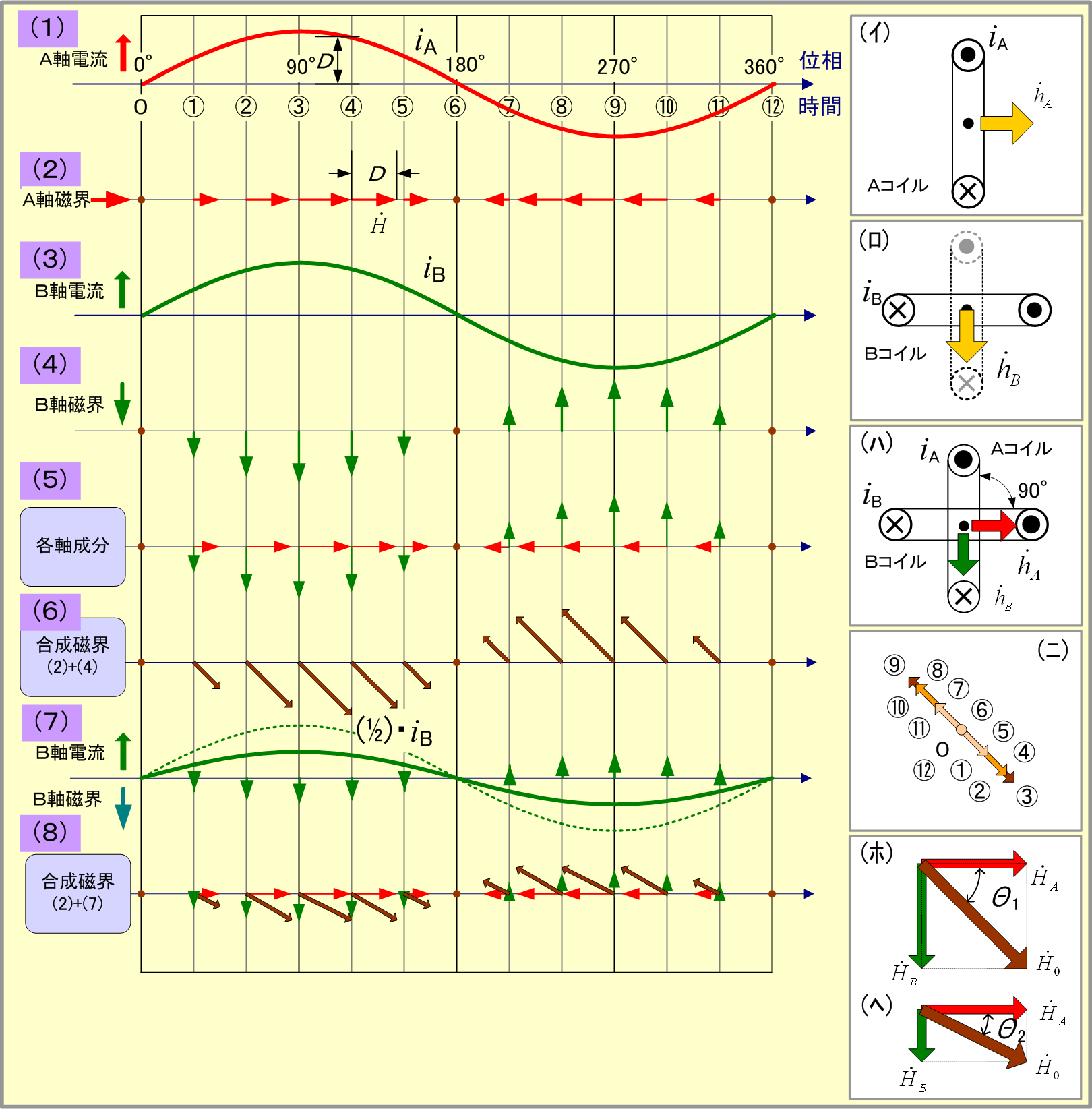
次に同図(ロ)のように、Aコイルと同じ仕様のBコイルを図のようにAコイルより時計方向に空間的に90°回転した位置に配置する。そして図(3)に示すようにAコイルと同じ大きさで、同じ位相の交流電流iBを流した場合の磁界
この場合、A、B両軸の磁界とその合成値は、共に同一周期で、正弦波状の時間的変化をしているので、三者の関係は静止ベクトルとして扱える。したがって、一般的にA、B両軸の磁界
また、図(7)のようにHBをHA/2とした場合は、合成磁界は図(8)で表示され、これらの関係を静止ベクトルで表すと図(ヘ)となり、
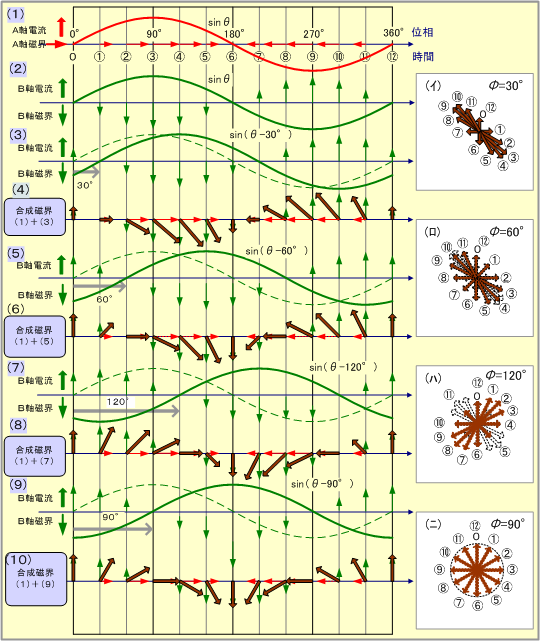
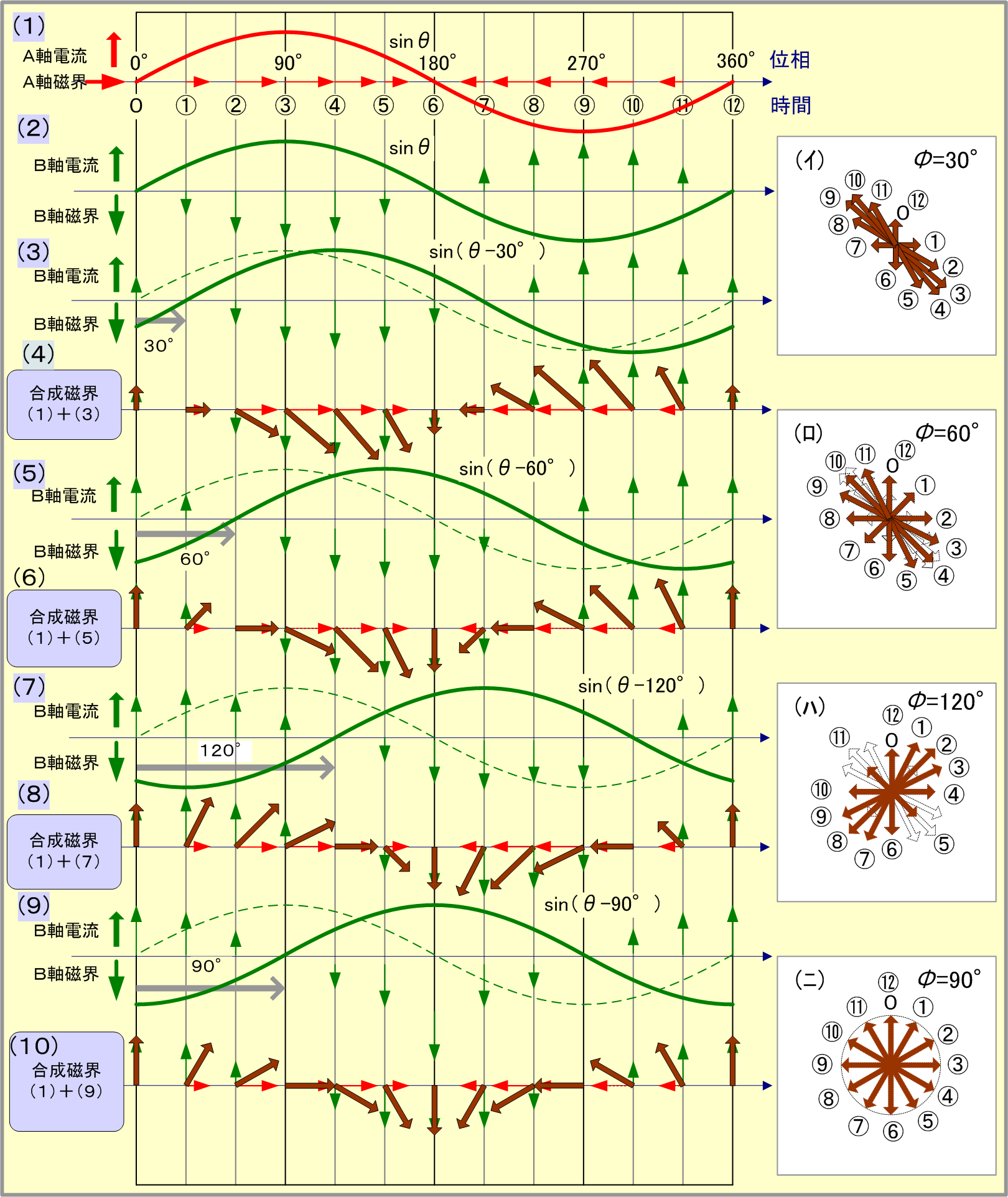
次にBコイルに流れる電流の位相を変えてみる。第3図の図(3)のようにB軸電流をA軸電流と同じ大きさで位相をA軸電流より30°遅らせてみると、合成磁界は図(4)となる。
続いて図(5)、図(7)にように遅れる位相角を60°、120°と増した場合、その合成磁界は図(6)、図(8)となり、右欄の図(イ)〜(ハ)に示すように、これらの合成磁界は大きさと回転速度が時間とともに変動する楕円状の回転磁界となる。図(9)のように遅れる位相角φを90°とすると、合成磁界は図(10)、図(ニ)となり、電流が1サイクル変化すると、磁界の大きさが常に一定で、一定回転速度で、時計方向に1回転する回転磁界ができる。
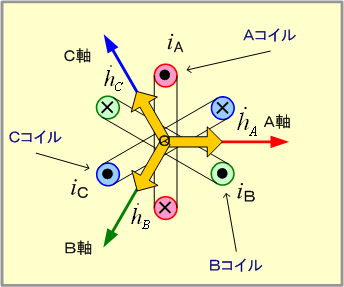
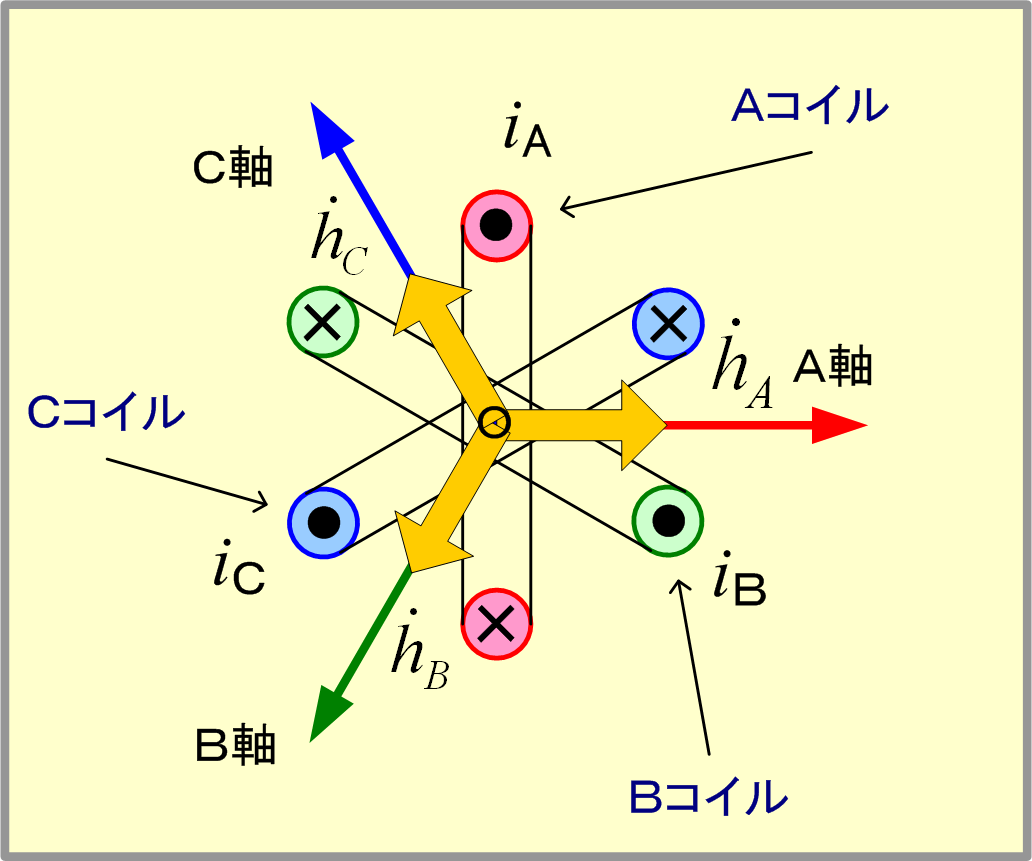
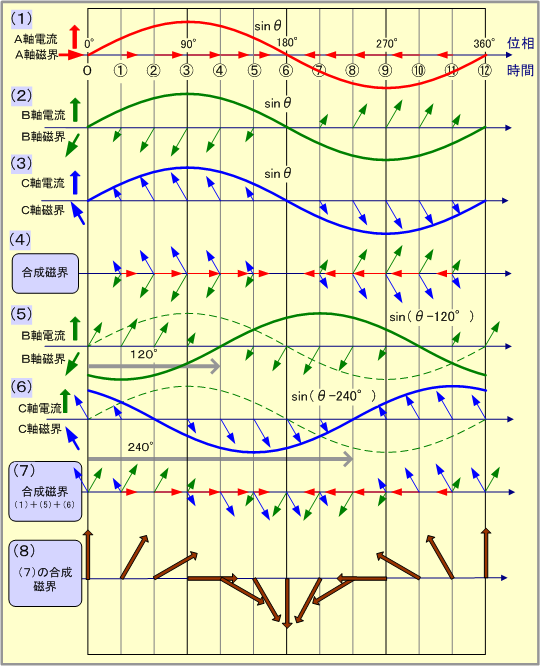
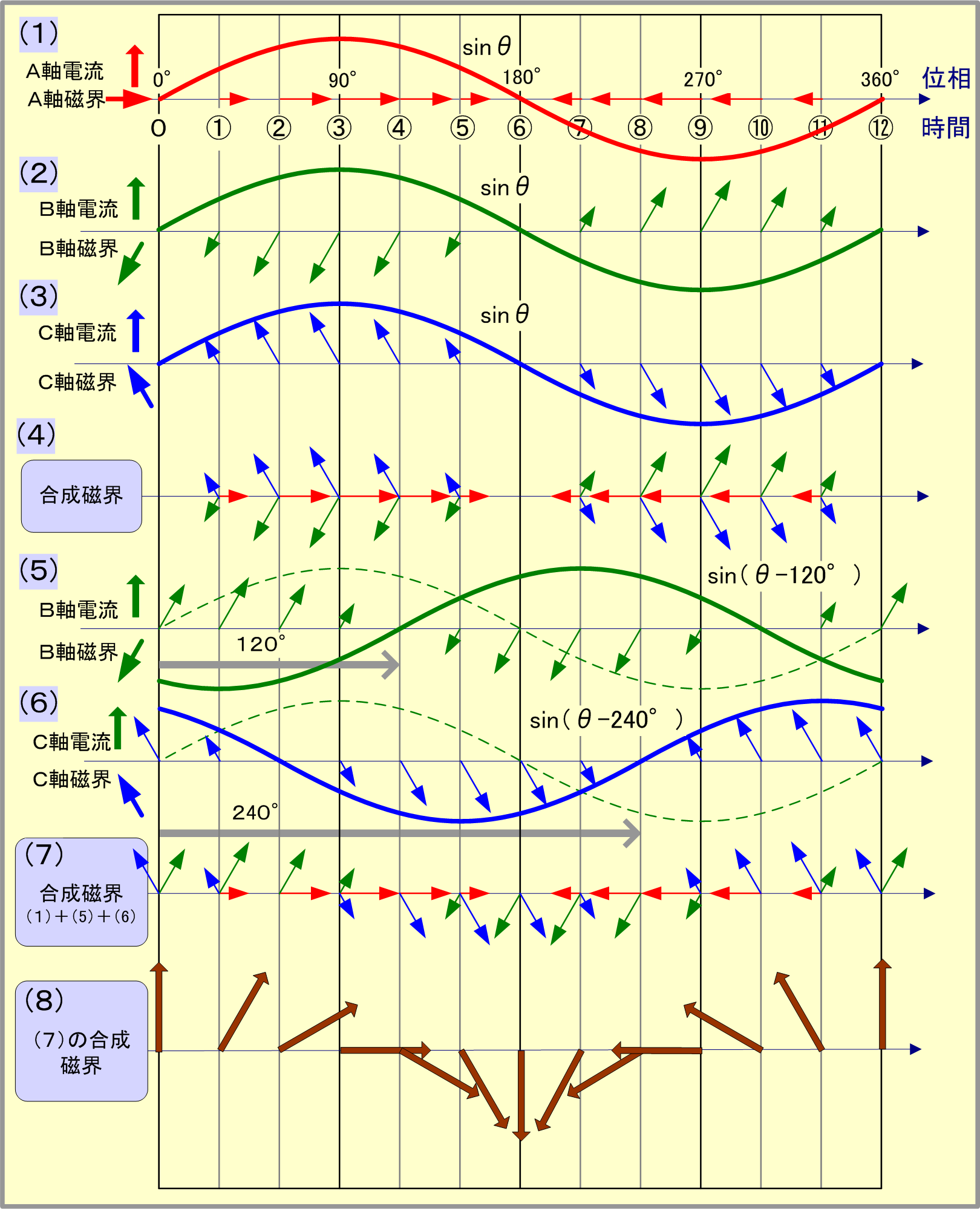
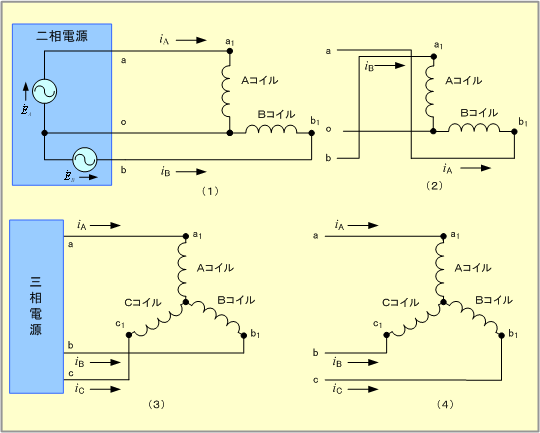
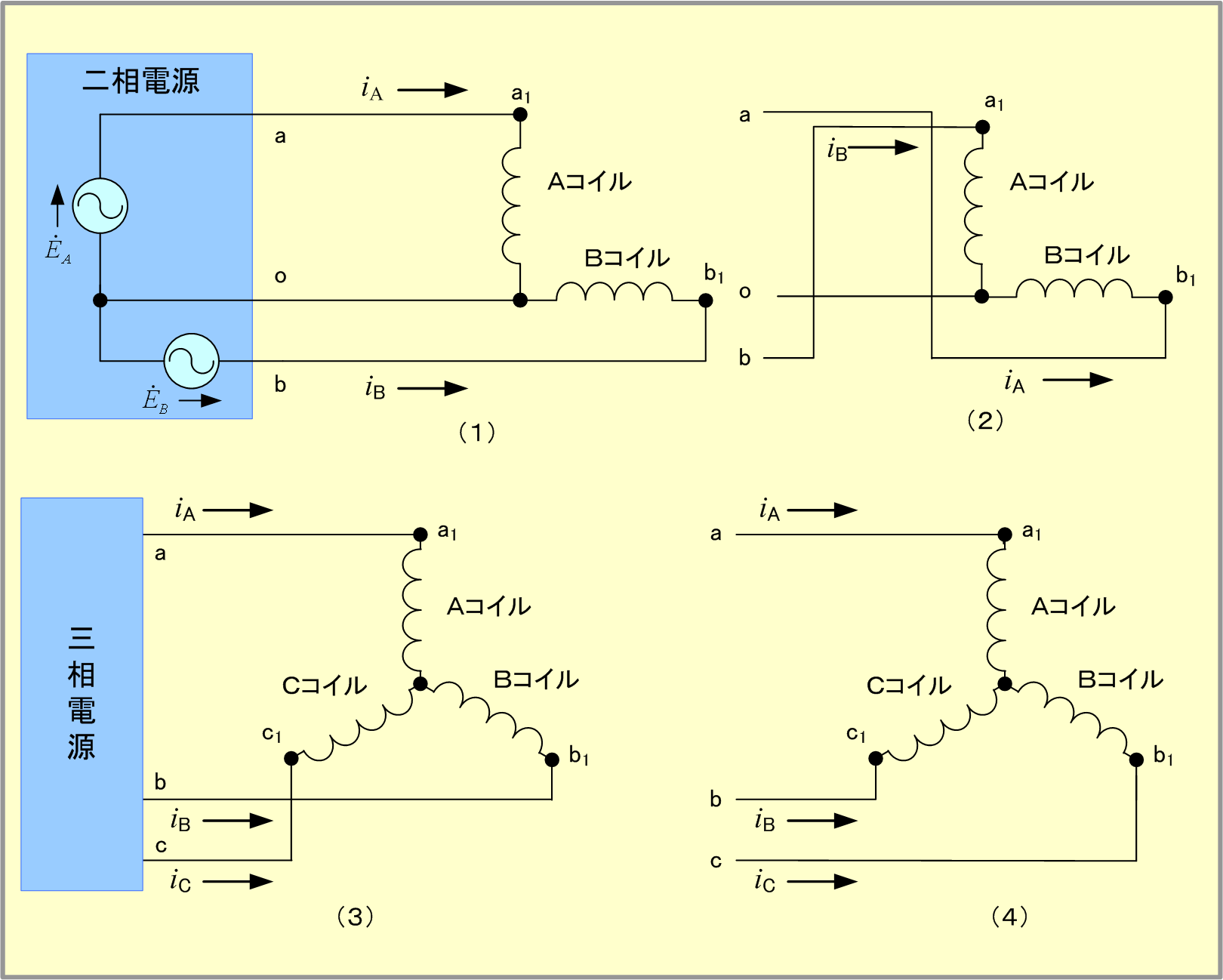
以上のことを予備知識として、各コイルに同相の電流を流した場合は、各軸電流と磁界の関係は第5図(1)〜(3)となり、3軸の磁界ベクトルは図(4)となるので、合成磁界はすべての位相(時間)で「零」となり、磁界はできない。
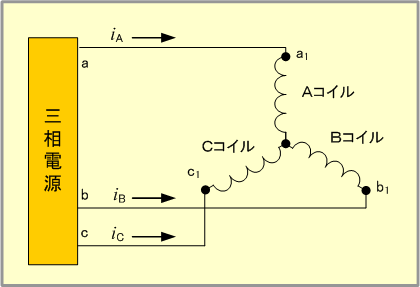
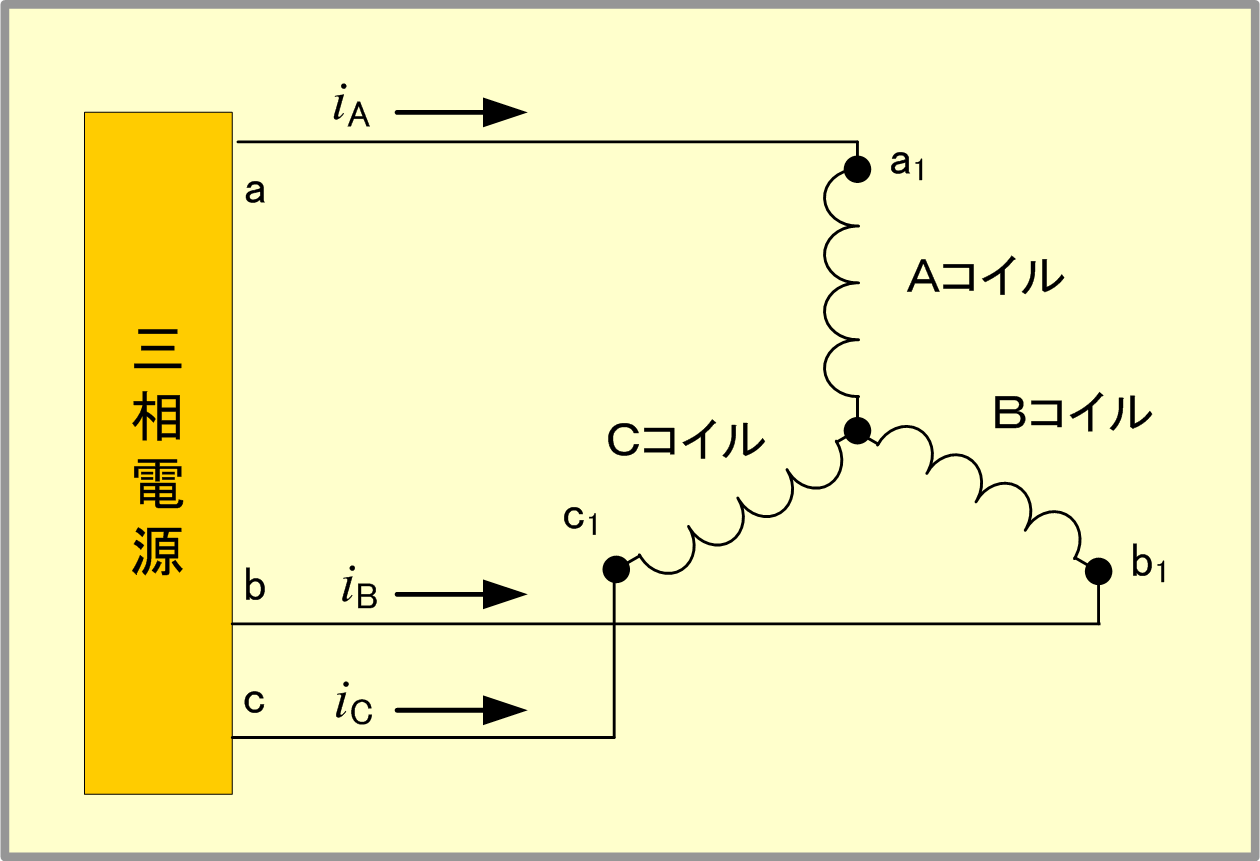
しかし、3個のコイルを第6図のように相順a、b、cの三相電源に接続し、そこに対称三相交流電圧を加えると、コイルの電流は大きさが同じで、相差が120°の対称三相交流となるので、B、C両軸の電流と磁界は、第5図の図(5)、(6)となり、3軸の磁界成分は同図(7)で、これらの磁界を合成すると図(8)となり、二相交流と同様に磁界の大きさ及び回転速度が一定で、電流1サイクルについて1回転する回転磁界となる。
[1]二相交流回転磁界
A、B両軸の磁界ベクトルを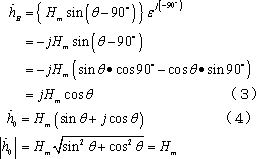
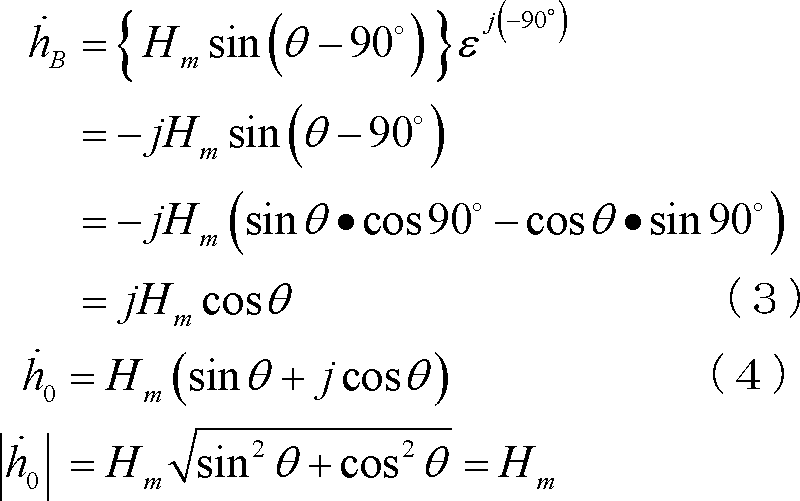
[2]三相交流回転磁界
A、B、C各軸の磁界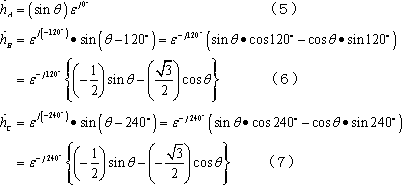
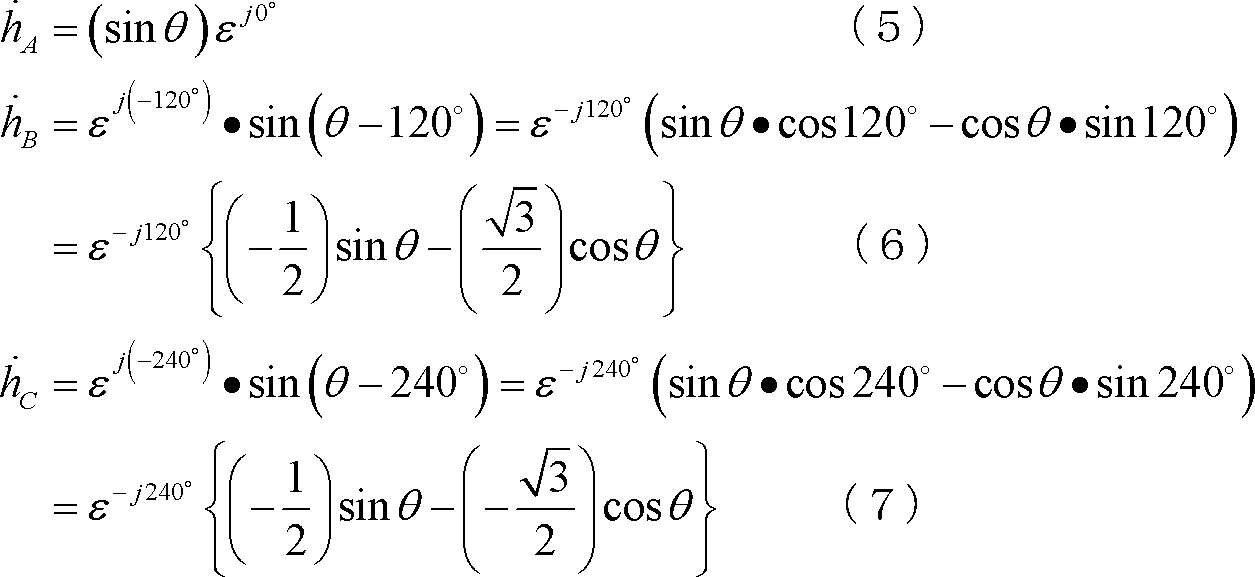
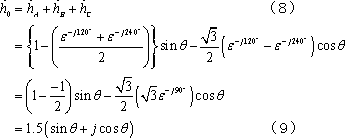
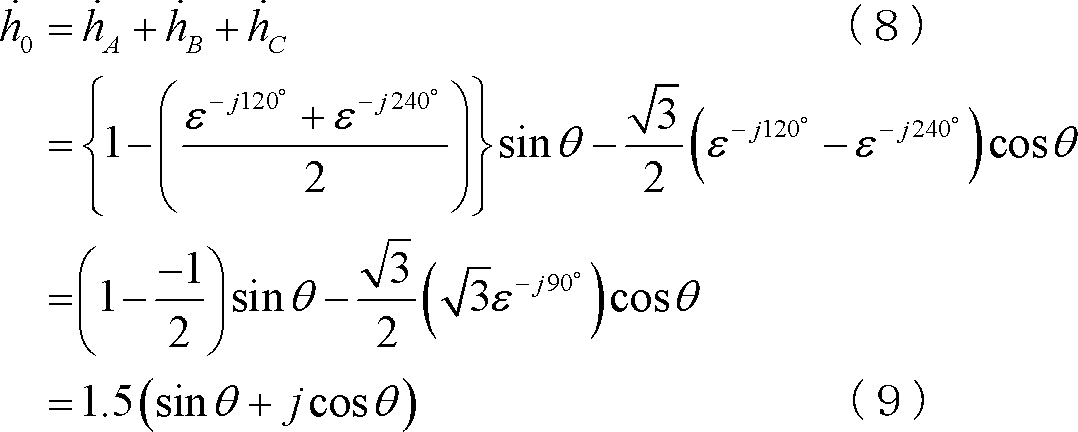
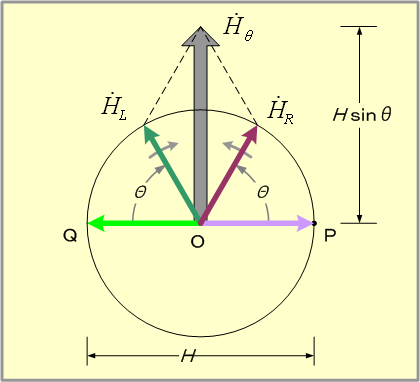
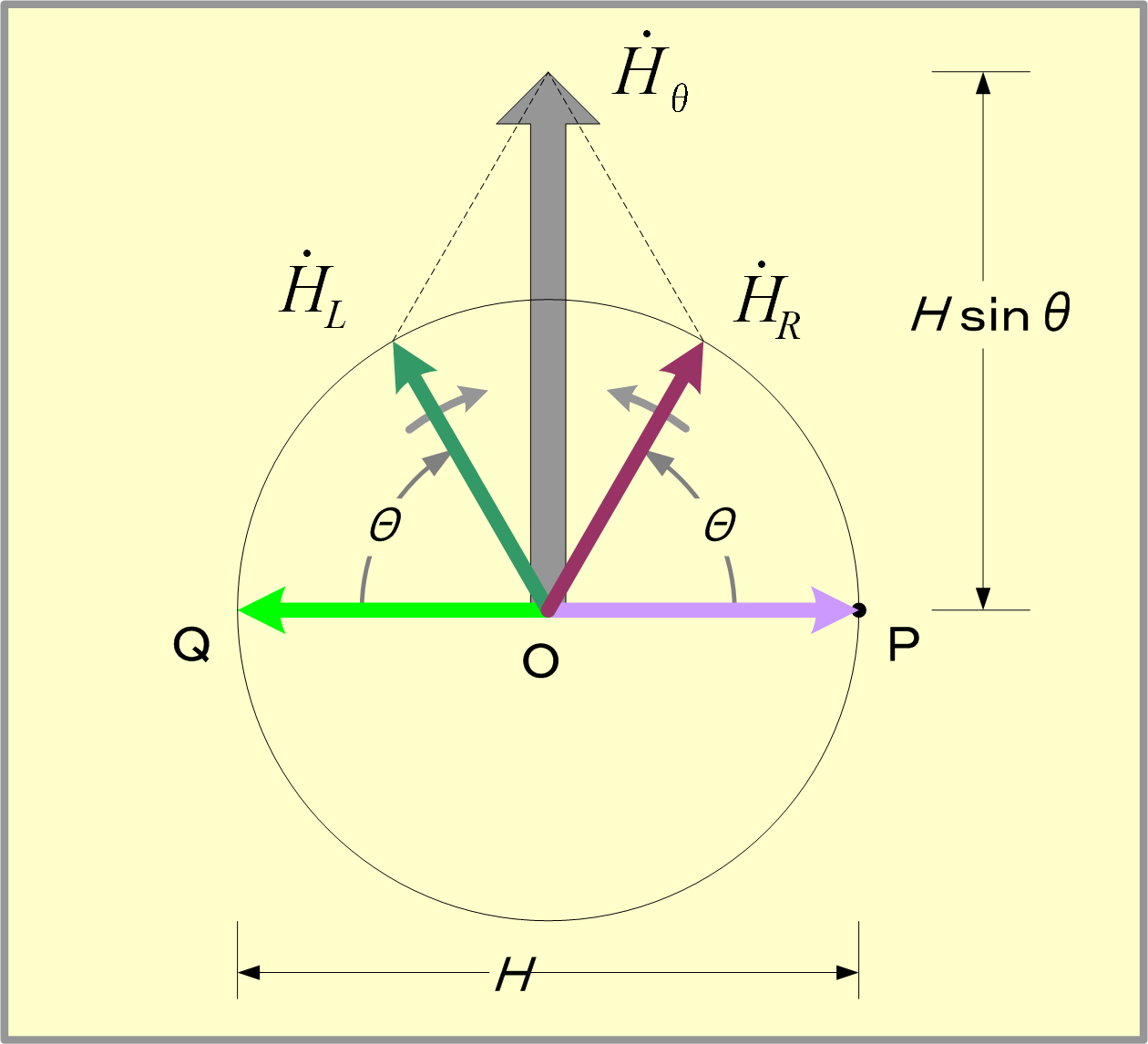
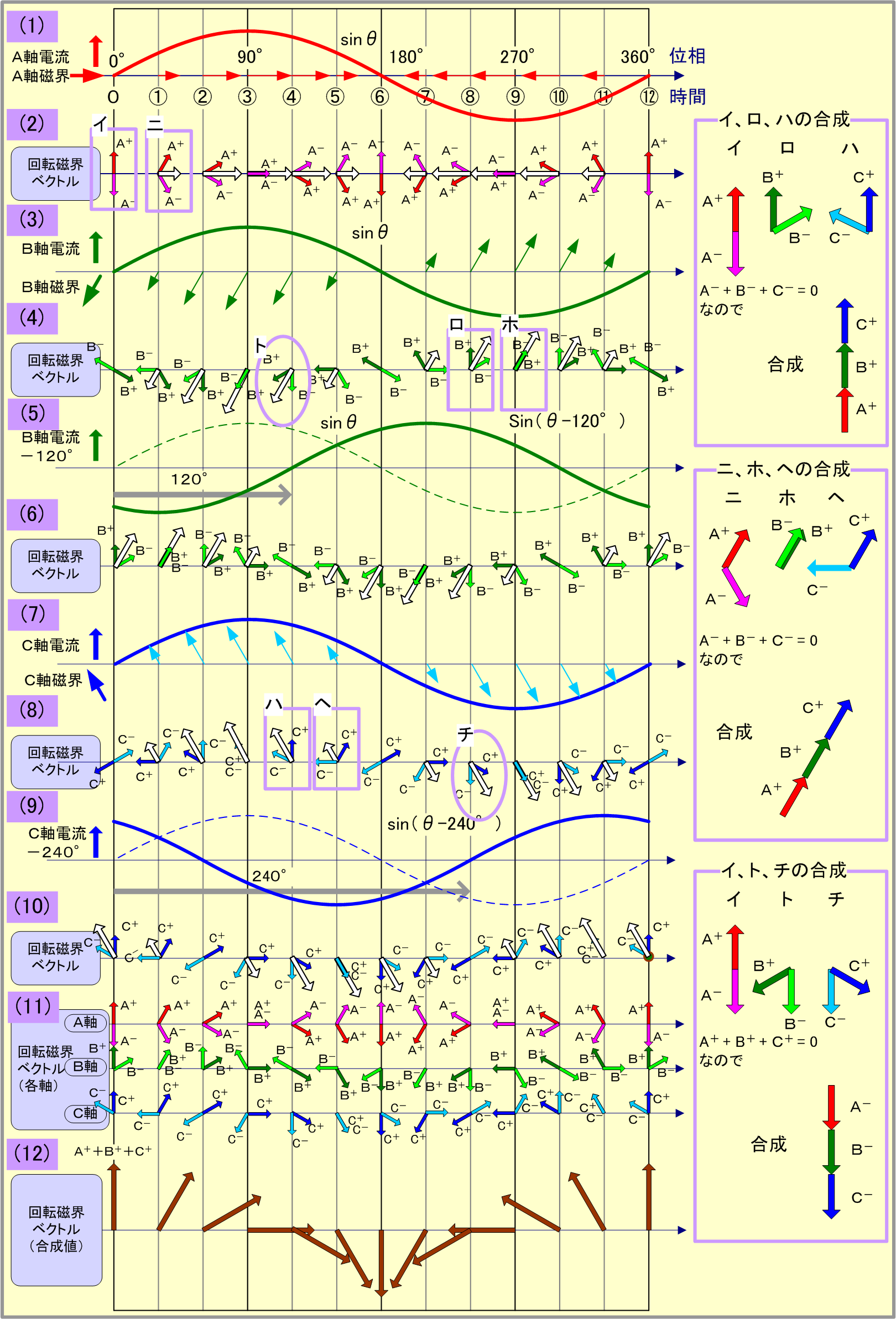
回転ベクトル法によれば、先に扱った二相交流による回転磁界は第8図のように説明される。まず、同図(1)のA軸磁界は、同軸の右(左)回転ベクトルをA+ (A-)とすれば図(2)のように、同図(3)のB軸磁界は、同軸の右(左)回転ベクトルをB+ (B-)とすれば図(4)のように、それぞれ回転ベクトルで表せる。図においてA軸磁界を表す図(2)の回転ベクトルで、θ=0の磁界(イ)と、図(4)のB軸回転ベクトルでθ=270°の磁界(ロ)とに注目し、両者を合成してみると、右欄のようにA++B+=2A+∠90°となる。同様にして、それより30°遅れた(ハ)と(ニ)を合成すると2A+∠60°となるので、以下、順次両軸磁界を合成すると、大きさが一定で30°ごとに右回転する磁界となっていることが分かる。
したがって、両軸の回転ベクトルを位相角θ=0から同じタイミングで両軸にもってくれば回転磁界が得られるはずで、このため図(1)のA軸電流に対してB軸電流を同じ大きさで図(3)の位相より270°進んだ(=90°遅れた)電流をB軸に流せば(図(5))B軸磁界として図(6)が得られ、その合成磁界成分は図(7)となり、その合成値は図(8)となる。この結果、図(8)から右回転の大きさが一定な回転磁界が時間が経過するにつれて位相角θに等しい空間角だけ連続的に回転する磁界(回転磁界)が現出することが分かる。
三相交流についても同様の見方ができる。すなわち、第9図で、3コイルに同相電流を流した場合、A軸の電流、磁界ベクトルは図(1)にB軸の電流、磁界ベクトルは図(3)に、C軸のそれは図(7)にそれぞれ表せる。また、これらの磁界ベクトルは回転ベクトル法によって図(2)、(4)、(8)のように回転ベクトルに置き換えられる。ここでθ=0°におけるA軸磁界である図(イ)に対して、θ=240°のB軸磁界(図(ロ))と、θ=120°のC軸磁界(図(ハ))とに注目し、この3磁界を合成すると右欄のようにA++B++C+=3A+∠90°となる。次にイ、ロ、ハよりそれぞれ30°遅れた各軸磁界ニ、ホ、ヘの合成値は右欄のように3A+∠60°となる。これから推測できるように、θ=0のときの磁界を、B軸ではA軸電流(sinθ)より240°進んだ位相の電流を、C軸ではA軸電流(sinθ)より120°進んだ位相の電流を流せばよいことを意味する。つまり、B軸電流の位相をA軸電流より120°遅らせ、C軸電流の位相をA軸電流より240°遅らせればよいわけで、これによってB、C軸の磁界は図(6)、(10)となり、3軸全体では図(11)の回転ベクトルとして表すことができ、その合成値は図(12)となって1軸の磁界大きさの1.5倍{=3×(1/2)}の回転磁界となる。
また、三相コイル2組を円周に配置した4極巻線の場合には、電流1サイクルで1組のコイル分回転するので、回転磁界は1/2回転する。
したがって、一般にP極巻線の場合は電流の周波数をf[Hz]とすれば、回転磁界は1秒間に(2/P)×f 回転するので、回転磁界毎分の回転速度Nは次式となる。
また、三相交流の場合は第9図で、B軸磁界として(ト)、C軸磁界として(チ)を採用すれば、その合成値は右欄となり左回転ベクトル3A-∠-90°が選択できる。したがって、B軸電流はA軸電流より120°位相の進んだ(=240°位相の遅れた)電流を、C軸電流は240°位相進んだ(=120°遅れた)電流を、それぞれ流してやればよい。具体的には第10図(3)の相順が abc の三相電源の場合、第10図(4)のように接続替えすればよい。
〜終わり〜
■ぜひアンケートにご協力下さい■