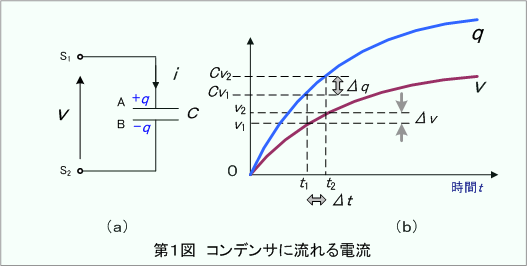
第1図(a)のように、静電容量C のコンデンサに電圧v が印加されている時、v
が(b)図のように時間と共に変化しているとすれば、時刻t1において、時間がt1からt2になるまでの間に、電圧がv1からv2に変化します。
したがって、図のように、t2−t1= Δt、v2−v1=Δv、とすれば、この間における電極の電荷変化Δq
は、
Δq=Cv2−Cv1=C(v2−v1)=CΔv
となるので、この間に流れる電流iは、その正方向を(a)図に示すように、印加電圧と同方向に選ぶと、次式となります。
![]() (1)
(1)
したがって、瞬時の電流について考えれば、
![]() (2)
(2)
となります。この結果、
コンデンサに流れる電流は、一般的に(2)式をもとに計算すればよいことになります。
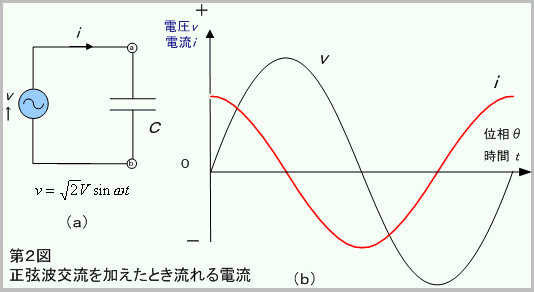
第2図(a)のように、正弦波交流電圧![]() が加えられている場合の電流iは、(2)式を使って、
が加えられている場合の電流iは、(2)式を使って、
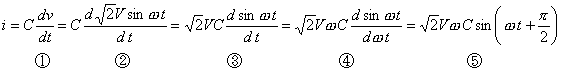 (3)
(3)
注: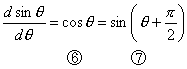 (4)
(4)
となります。
したがって、(b)図のiに示すように、コンデンサでは、印加されている正弦波交流電圧より90°位相の進んだ正弦波電流が流れます。
第3図において、C に流れる電流の意味をジックリ理解しておきましょう。
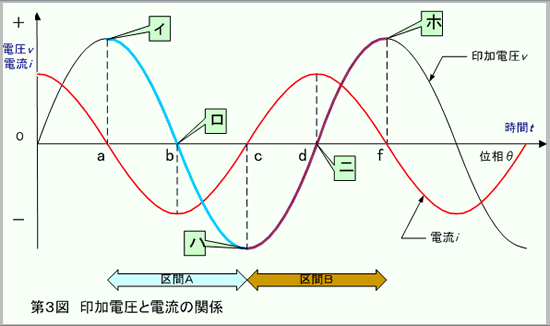
同図において、区間Bは時間に対して電圧が増加している状態、区間Aは逆に減少している状態なので、電流は、区間Bでは正方向(第2図(a)の矢印方向)に、区間Aでは矢印と反対の方向に流れます。
電圧と電流との量的な関係は、(3)式の㈭から 、![]() の関係にあるので、電流の実効値をIとすれば、
の関係にあるので、電流の実効値をIとすれば、
![]() (5)
(5)
または、 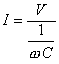 (6)
(6)
の関係にあります。
したがって、電流の大きさを決める要素は、![]() で、これを容量リアクタンスXCと呼んでいます。
で、これを容量リアクタンスXCと呼んでいます。
次回は、直流回路においてコンデンサにどんな電流が流れるか等について解説します。


