~終わり~
■ぜひアンケートにご協力下さい■


三相回路の計算は単相回路の計算に比べて複雑となるが、電源電圧の大きさが同一で、位相差が互いに120°で、負荷各相のインピーダンスが等しい場合は、回路各相の電圧や電流が、大きさが等しく位相差が120°の交流(対称三相交流)となるため、いわゆる三相平衡回路となり、等価単相回路の計算で対応する。しかし、各相の電圧や回路定数が不ぞろい、断線、短絡、地絡などの事故・故障などのときは、各相の電圧・電流がアンバランスとなり(三相不平衡回路)、その回路計算は複雑となる。
対称座標法はこのような三相不平衡回路の計算を平衡回路に直して計算する巧妙な計算法である。しかし、その反面、ユニークな考え方をするため、その扱いに手を焼くことも多く見受けられる。そこで、今回はこの独特な計算法を攻略するため、対称座標法とはどんな計算法なのか、計算の根拠となる考え方をジックリと考察する。
まずは本項のタイトルを図で実感してもらいたい。電圧を例にとると、第1図(1)に示す三相交流電圧は、A、B、C各相の電圧の大きさが同一で、その位相差も120°である。このように各相の電圧の大きさが等しく、相差が120°の三相電圧を対称三相交流電圧という。
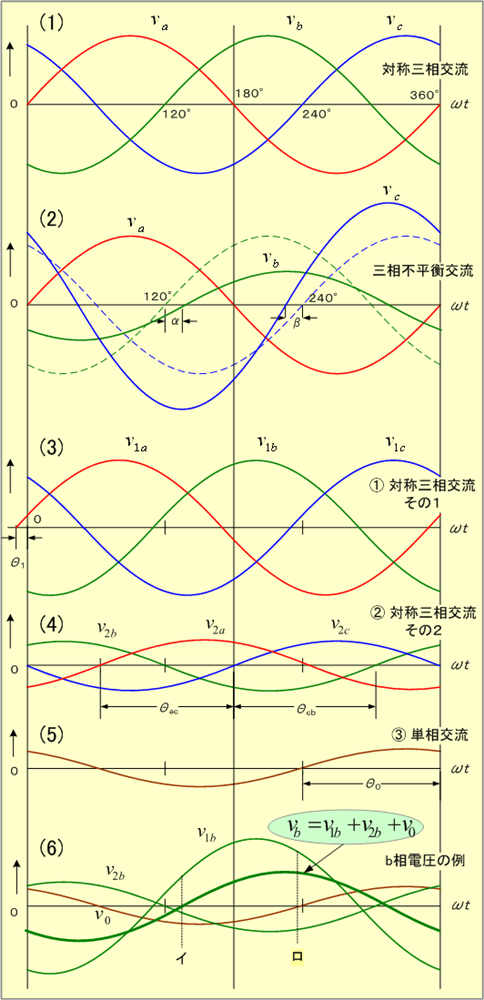

第1図 三相交流回路の電圧波形
第1図(2)に示す三相交流電圧は、A、B、C各相の電圧の大きさが同一でなく、その位相差も120°でない、三相不平衡電圧であるが、これらの電圧は、『第1図(3)、(4)、(5)に示す交流で表せる』という。第1図(3)と(4)は対称三相電圧、第1図(5)は単相電圧であるから、元の電圧波形は、『2組の対称三相交流電圧と1個の単相電圧で表せる』ことになる。念のため、B相の電圧を例に調べると、第1図(6)となり、その関係が成立していることが確認できる。
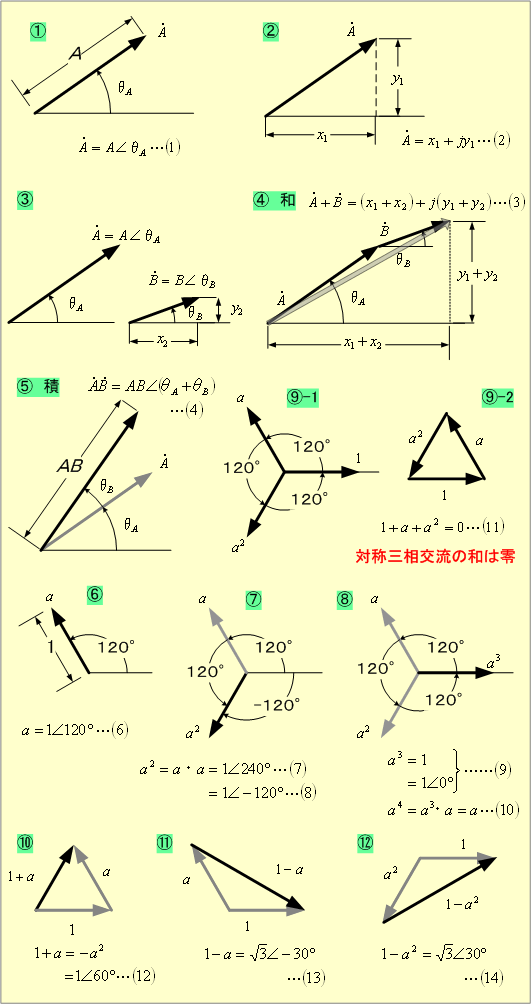
前述の事実を式で表してみよう。それには第2図で、ベクトルの基本的な性質を再確認し、![]()
![]() とその性質を理解しておくことが必要である。
とその性質を理解しておくことが必要である。
![]()
![]() は「大きさが1で、偏角が120°のベクトル」で、これをベクトルオペレータと呼び、
は「大きさが1で、偏角が120°のベクトル」で、これをベクトルオペレータと呼び、![]()
![]() と表記している。
と表記している。![]()
![]() はこれから多用するので、第2図で
はこれから多用するので、第2図で![]()
![]() の性質をよく理解しておいてほしい。
の性質をよく理解しておいてほしい。

第2図
以上を予備知識として本題に入る。なお、これからの内容はすべてa相をベースに考える。
第1図において、図(3)のa相電圧v1aを![]()
![]() と記号法で表示すれば、b相電圧v1bは
と記号法で表示すれば、b相電圧v1bは![]()
![]() 、c 相電圧v1cは
、c 相電圧v1cは![]()
![]() と、それぞれ表示できる。
と、それぞれ表示できる。
同様に、同図(4)のa相電圧v2aを![]()
![]() と表示すれば、b相電圧v2bは
と表示すれば、b相電圧v2bは![]()
![]() 、c 相電圧v2cは
、c 相電圧v2cは![]()
![]() と、それぞれ表示できる。また、同図(5)の単相電圧v0 は
と、それぞれ表示できる。また、同図(5)の単相電圧v0 は![]()
![]() と表示する。
と表示する。
したがって、実際のA、B、C各相の電圧va 、vb 、vcを![]()
![]() 、
、![]()
![]() 、
、![]()
![]() と記号法で表示すれば、これらの電圧は、
と記号法で表示すれば、これらの電圧は、
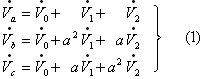
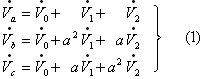
として表すことができる。
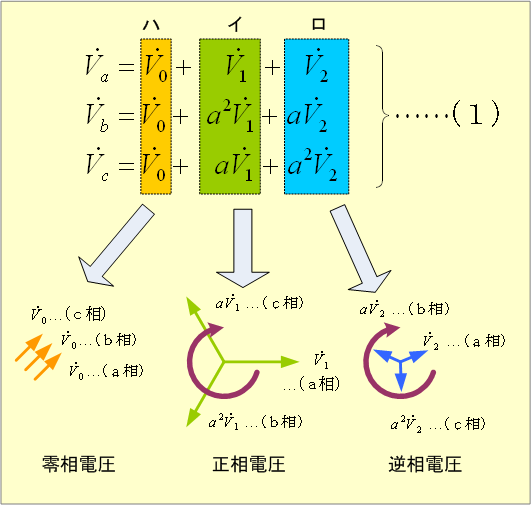

第3図 (1)式の図示
(1)式を図で表した第3図において、右辺第2項(点線部イ)に注目すると、A、B、C各相の電圧は![]()
![]() 、
、![]()
![]() 、
、![]()
![]() で、A相の電圧は
で、A相の電圧は![]()
![]() で、B相の電圧は
で、B相の電圧は![]()
![]() 、つまりA相と同じ大きさでA相より120°遅れた電圧であり、C相の電圧は
、つまりA相と同じ大きさでA相より120°遅れた電圧であり、C相の電圧は![]()
![]() 、つまりA相と同じ大きさでA相より240°遅れた電圧であることが分かる。
、つまりA相と同じ大きさでA相より240°遅れた電圧であることが分かる。
これら三つの電圧は電源の相回転と同じ対称三相交流電圧であり、![]()
![]() は電源の相回転と同じ相回転、つまり正の相回転の対称三相電圧をつくり出す元となっている電圧という意味から正相電圧と呼ぶことにする。
は電源の相回転と同じ相回転、つまり正の相回転の対称三相電圧をつくり出す元となっている電圧という意味から正相電圧と呼ぶことにする。
これに対して、右辺第3項(点線部ロ)の電圧は、A相から順に![]()
![]() 、
、![]()
![]() 、
、![]()
![]() となっているので、120°位相の遅れる順序、つまり相順がA、C、Bで、電源本来の相回転A、B、Cとは逆な相回転の対称三相電圧であり、
となっているので、120°位相の遅れる順序、つまり相順がA、C、Bで、電源本来の相回転A、B、Cとは逆な相回転の対称三相電圧であり、![]()
![]() はその元となっている電圧という意味から、正相電圧にならって逆相電圧と呼ぶ。
はその元となっている電圧という意味から、正相電圧にならって逆相電圧と呼ぶ。
残る右辺第1項(点線部ハ)は、各相とも同じ![]()
![]() である。ということは、各相共に同じ大きさで同じ位相の電圧であり、この電圧
である。ということは、各相共に同じ大きさで同じ位相の電圧であり、この電圧![]()
![]() は、先の
は、先の![]()
![]() や
や![]()
![]() のように相回転を伴わない、つまり相回転のない(相回転が零の)電圧という意味から零相電圧と呼ぶことにする。なお、以後は正相電圧、逆相電圧、零相電圧を総称して対称分電圧と呼ぶ。
のように相回転を伴わない、つまり相回転のない(相回転が零の)電圧という意味から零相電圧と呼ぶことにする。なお、以後は正相電圧、逆相電圧、零相電圧を総称して対称分電圧と呼ぶ。
次に(1)式のような巧妙な関係がなぜ成立するのであろうか。ベクトルを使って調べてみよう。
第4図において回路電圧![]()
![]() 、
、![]()
![]() 、
、![]()
![]() が 第4図(1)のようであるとき、
が 第4図(1)のようであるとき、
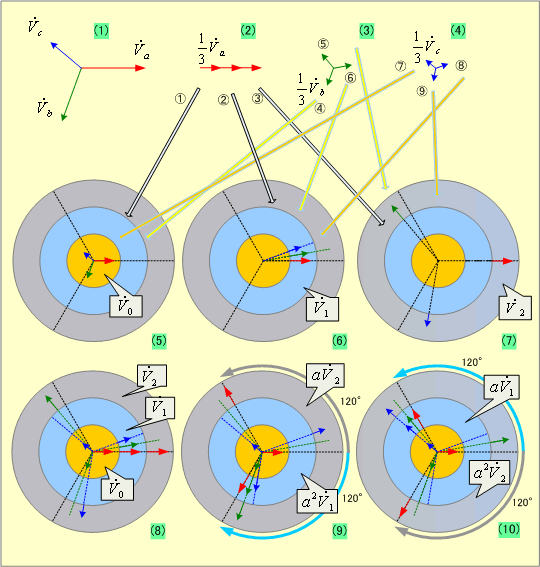

第4図 各相電圧と対称分電圧との関係
![]()
![]() まず、
まず、![]()
![]() を3個((2)図)、
を3個((2)図)、![]()
![]() を含む対称三相交流((3)図)、
を含む対称三相交流((3)図)、![]()
![]() を含む対称三相交流((4)図)、をそれぞれ用意する。
を含む対称三相交流((4)図)、をそれぞれ用意する。
![]()
![]() これらのベクトルを(5)、(6)、(7)図のように三つのグループに分け、(5)図のグループを
これらのベクトルを(5)、(6)、(7)図のように三つのグループに分け、(5)図のグループを![]()
![]() 、(6)図のそれを
、(6)図のそれを![]()
![]() 、(7)図のそれを
、(7)図のそれを![]()
![]() と呼ぶことにする。
と呼ぶことにする。
(8)図はこれら三つのグループをすべてまとめたもので、これらをすべて加えると、各グループには![]()
![]() があり、このほかのベクトルはすべて打ち消し合っているので、これらのベクトル和は
があり、このほかのベクトルはすべて打ち消し合っているので、これらのベクトル和は![]()
![]() に等しい。つまり、
に等しい。つまり、
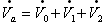
の関係にある。
次にグループ![]()
![]() と、「グループ
と、「グループ![]()
![]() のベクトルをすべて120°遅らせたもの」と、「グループ
のベクトルをすべて120°遅らせたもの」と、「グループ![]()
![]() のベクトルをすべて120°進めたもの」とを加えてみると(9)図となり、同図の各グループからは
のベクトルをすべて120°進めたもの」とを加えてみると(9)図となり、同図の各グループからは![]()
![]() が選択され、ほかのベクトルは互いに打ち消し合うので、
が選択され、ほかのベクトルは互いに打ち消し合うので、
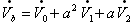
が成立する。
次にグループ![]()
![]() と、「グループ
と、「グループ![]()
![]() のベクトルをすべて120°進めたもの」と、「グループ
のベクトルをすべて120°進めたもの」と、「グループ![]()
![]() のベクトルをすべて120°遅らせたもの」とを加えてみると(10)図となり、同図の各グループからは
のベクトルをすべて120°遅らせたもの」とを加えてみると(10)図となり、同図の各グループからは![]()
![]() が選択され、ほかのベクトルは互いに打ち消し合うので、
が選択され、ほかのベクトルは互いに打ち消し合うので、
の関係にある。以上が各相の電圧が(1)式の関係にあることのベクトルによる説明である。
それではこのような変換がなぜ可能なのか、その仕組みをもう少し詳しく調べてみよう。
第5図は1個のベクトル![]()
![]() に三つの位相操作を試みた図を示す。図のようにベクトル
に三つの位相操作を試みた図を示す。図のようにベクトル![]()
![]() を3個用意し、ステージ(イ)の0 I II の各欄に置く。
を3個用意し、ステージ(イ)の0 I II の各欄に置く。
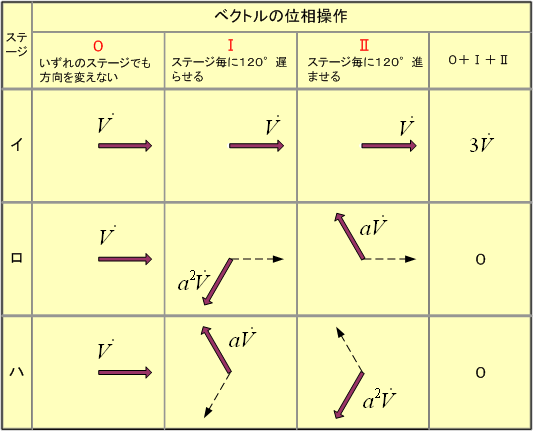

第5図 ベクトルの位相操作
位相操作の0系ではステージが変わってもベクトルの方向は変えない。 I 系では現ステージのベクトルを120°遅らせて次ステージに描く。II 系では I 系とは逆に現ステージのベクトルを120°進ませて次ステージに描く。ベクトルにこのような位相操作を加えると、ステージは(イ)、(ロ)、(ハ)と進み、次は(イ)と同じベクトル関係に戻ることが分かる。したがって、このようなベクトル操作では三つのステージしかなく、各ステージのベクトル和は図の右欄に示したように各系のベクトルの方向が同じ場合だけ3![]()
![]() となり、そのほかのステージでは対称三相交流の和となるので零となる。
となり、そのほかのステージでは対称三相交流の和となるので零となる。
それでは第5図の関係を応用して第6図で、同図下段の各相電圧について対称分電圧で表すことを考えてみよう。
まず、a相電圧![]()
![]() は第5図の
は第5図の![]()
![]() を
を![]()
![]() に置き換えて第6図の該当欄に描く。この結果、ステージの合成値はステージ(イ)だけが
に置き換えて第6図の該当欄に描く。この結果、ステージの合成値はステージ(イ)だけが![]()
![]() で、他ステージは零となる。
で、他ステージは零となる。
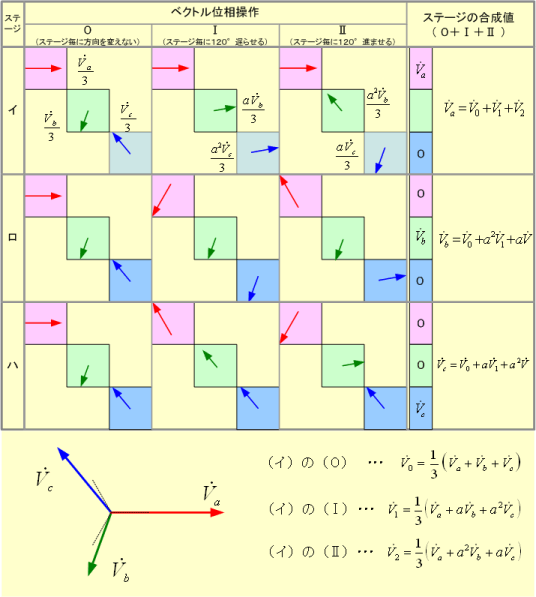

第6図 各相電圧と対称分電圧の取り出し方
次に![]()
![]() と同じ手法でステージの合成値がステージ(ロ)で
と同じ手法でステージの合成値がステージ(ロ)で![]()
![]() となるようもくろんでみる。つまり、第5図で
となるようもくろんでみる。つまり、第5図で![]()
![]() を
を![]()
![]() に置き換え、第5図のステージ(イ)が第6図のステージ(ロ)に現れるようすればb相関係の電圧ベクトルは該当欄のようになる。
に置き換え、第5図のステージ(イ)が第6図のステージ(ロ)に現れるようすればb相関係の電圧ベクトルは該当欄のようになる。
残るc 相電圧についても同様で、ステージの合成値がステージ(ハ)で![]()
![]() となるようにベクトルを配置すれば第6図が完成する。
となるようにベクトルを配置すれば第6図が完成する。
この結果、![]()
![]() 、
、![]()
![]() 、
、![]()
![]() は各ステージの合成値(第6図右欄の左側の値)から求められる。いま、a相をベースに考えて、ステージ(イ)において0系のベクトル群を
は各ステージの合成値(第6図右欄の左側の値)から求められる。いま、a相をベースに考えて、ステージ(イ)において0系のベクトル群を![]()
![]() 、 I 系のベクトル群を
、 I 系のベクトル群を![]()
![]() 、 II 系のベクトル群を
、 II 系のベクトル群を![]()
![]() とそれぞれおけば、これらの内容は、ステージ(イ)における各系のベクトルの値から、第6図下段のようになるので、次の(2)式で表されることが分かる。
とそれぞれおけば、これらの内容は、ステージ(イ)における各系のベクトルの値から、第6図下段のようになるので、次の(2)式で表されることが分かる。
また、各相の電圧は、これら![]()
![]() 、
、![]()
![]() 、
、![]()
![]() を使うことで第6図右欄の式で表され、(1)式と同一であることが確認できる。と同時に、(
を使うことで第6図右欄の式で表され、(1)式と同一であることが確認できる。と同時に、(![]()
![]() ,
,![]()
![]() ,
,![]()
![]() )は相回転abc の、(
)は相回転abc の、(![]()
![]() ,
,![]()
![]() ,
,![]()
![]() )は相回転acb の、それぞれ対称三相電圧であり、
)は相回転acb の、それぞれ対称三相電圧であり、![]()
![]() は単相交流電圧であることが分かる。
は単相交流電圧であることが分かる。
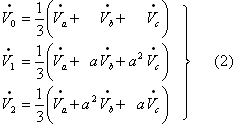
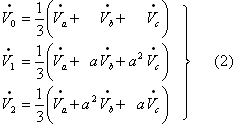
以上は電圧の例であるが、電流についても同様な取り扱いができる。したがって、実際の各相電流![]()
![]() 、
、![]()
![]() 、
、![]()
![]() に対して、正相電流
に対して、正相電流![]()
![]() 、逆相電流
、逆相電流![]()
![]() 、零相電流
、零相電流![]()
![]() を考えて回路の計算が行われる。
を考えて回路の計算が行われる。
以上のことから、第6図で扱ったように不平衡交流である各相の交流を、『対称三相交流の和は零』であるという関係を巧みに利用して2個の対称三相交流と1個の単相交流に置き換え、三相不平衡回路を対称交流回路と単相回路で扱おうというのが対称座標法である。
したがって、対称座標法という計算法の計算過程は次のようになる。
ことになる。
このような考え方による回路計算法が対称座標法であり、その計算の流れは第7図で表されることになる。
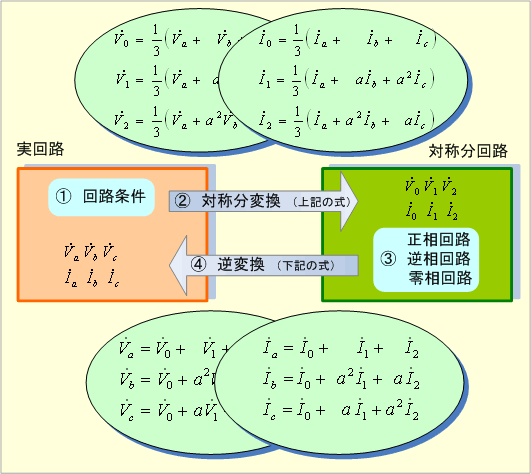

第7図 対称座標法の計算フロー
