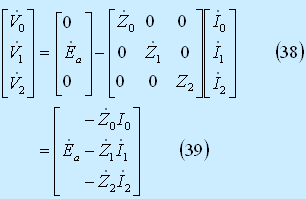三相回路は基本的には電源として対称三相交流を発生する三相交流発電機があり、これに三相負荷が線路でつながれるので、第１図のような構成となっている。

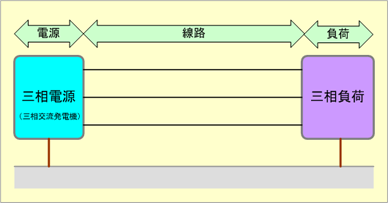
第１図　三相回路の構成

　それでは電源回路から順次調べてみよう。

　電源は三相交流発電機が中心で、同機は対称三相交流電圧を発生する起電力と内部インピーダンス から成る第２図（１）のような回路を形成している。

① 発電機で発生する起電力は、相回転がａ、ｂ、ｃの対称三相交流電圧で、各相の電圧は と表されるので、次式で示される。

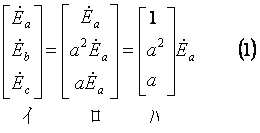
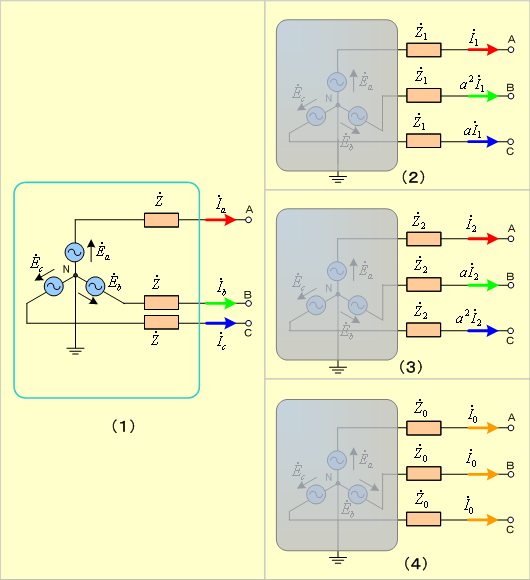
第２図　各相電流による発電機内の電圧降下

② 発電機回路内の各相電流によって生ずる電圧降下ｖは、対称分電流で考えれば
(1) 各相に正相電流が流れたときの電圧降下は、同図（２）に示すように、発電機内に正相電流が流れることで 生ずるインピ ーダンス降下の原因となるインピーダンスを正相インピーダンスと呼び、これを とすれば、 正相インピーダンスと各相の正相電流の積で求められる。
(2) 同様に逆相電流が流れたときの電圧降下は、同図（3）に示すように、逆相インピーダンスを とすれば、逆相インピ ーダンスと逆相電流の積で求められる。
(3) 発電機の各相に零相電流が流れたときの電圧降下は、同図（4）のように、零相インピーダンスをとすれば、零 相インピーダンスと零相電流の積で計算でき、各相とも等しい 。

以上の結果、電圧降下は第１表のようになる。

第１表　各相の電圧降下

相	正相		逆相		零相
	電流	電圧降下	電流	電圧降下	電流	電圧降下
A相
B相
C相

したがって、発電機回路内の電圧降下は次式で表される。

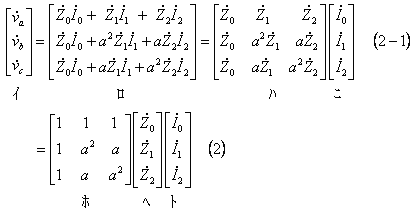
③ この結果、発電機の端子電圧Ｖの対称分への変換Ｖ‘ は、（３）式から（４）式の経過により（５）式のように計算できる。

Ｖ‘＝ＣＶ＝Ｃ（E－ｖ）＝ＣＥ－Ｃｖ　　　(３)
　　＝Ｅ‘－ｖ‘　　　(４)

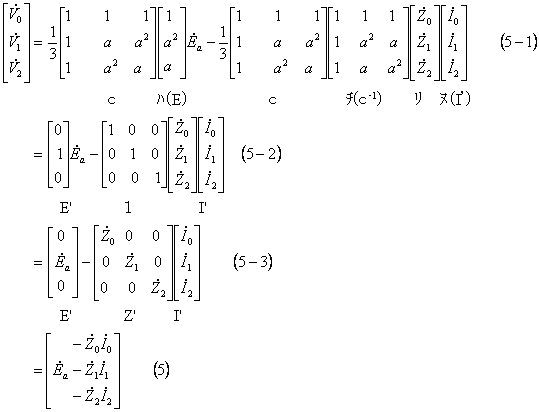
　したがって、発電機回路の対称分回路は第３図のようになる。ここで①～③図に示す各式は各対称分回路の計算式である。（５－３）式または（５）式のことを 交流発電機の基本式 という。

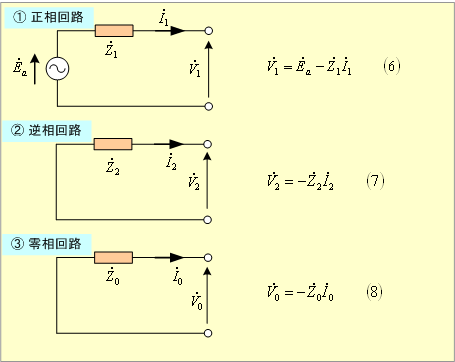
第３図　発電機回路の対称分回路

④ 電源の中性点接地について
　 もし発電機の中性点が第４図（１）のようにインピーダンス で接地されている場合は、各相の零相電流 が第４図（２）の点線経路で流れるため、（９-1）式が成立し、

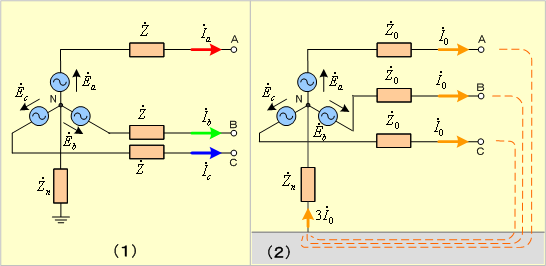
第４図　発電機の中性点にインピーダンスが接続された場合の零相回路

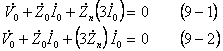
零相回路では（１０）式の関係が成立する。

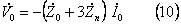
このため零相に関する対称分回路は第５図となる。

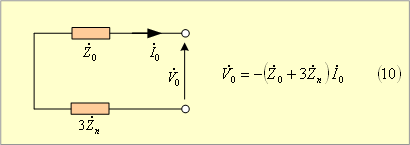
第５図　対称分零相回路

　第６図のような三相線路におけるＰＱ間での線路インピーダンスによる電圧降下は、ａ、ｂ、ｃ各相の線路インピーダンスを とすれば、（１１）式で示される。

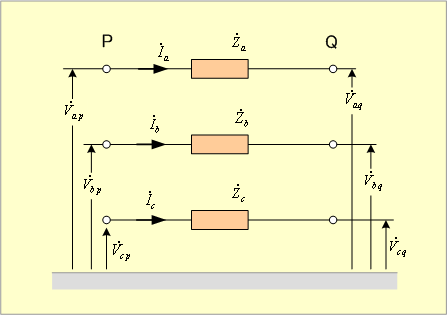
第６図　三相線路の電圧降下

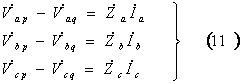
これを行列で表示すると

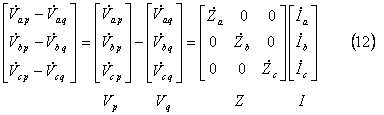
となる。ここで送電線路のようにねん架が充分行われている線路では、 なので、これを とおき、線間の相互インダクタンスも各相間等しいとみなせるので、これを とすれば、 （１２）式は、

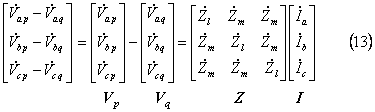
となる。
　ここで（１３）式を対称分変換する。それには（１３）式を、
　　　Ｖｐ－Ｖｑ＝ＺＩ　　　（14）
とみて、上式を対称分変換すると、
　左辺　Ｖ‘＝Ｃ（Ｖｐ－Ｖｑ）＝ＣＶｐ－ＣＶｑ＝Ｖｐ’－Ｖｑ’ 　 （15）
　右辺　＝ＣＺ（Ｃ^－１Ｉ’）＝（ＣＺＣ^－１）Ｉ’　　　　　　　　　（16）
となり、対称分回路では、
　Ｖ’＝（ＣＺＣ^－１）Ｉ’ 　　　（17）
の関係にあることが分かる。したがって、対称分回路でのインピーダンスをＺ‘ とすれば、 Ｚ‘ は、次のようにして求めることができる。

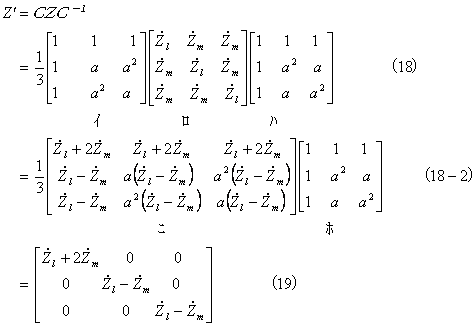
　この結果、線路での電圧降下の式である（１３）式に対応して、対称分回路では次の式が成立する。

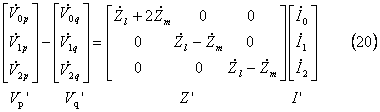
　Ｚ’が対角行列であることは、注目すべき内容である。すなわち、これは各対称分ごとに独立した回路で扱えることを意味している。
　なお、Ｚ’ の各要素がどうしてこのような値となるかを別の面から調べてみよう。

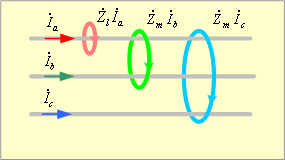
第７図　線間の相互インダクタンスによる電圧降下

　第７図で、ａ相におけるインピーダンス降下は、ａ相電流によるインピーダンス降下、ｂ相電流の相互誘導作用によるインピーダンス降下、ｃ相電流の相互誘導作用によるインピーダンス降下の和であり、（２１）式が成立する。

このため正相電流 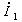によるインピーダンス降下 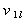は、

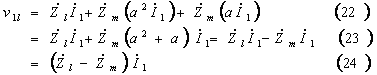
逆相電流 によるインピーダンス降下 は、

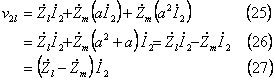
零相電流 によるインピーダンス降下 は、

　　　　

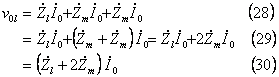
となる。したがって、次式が成立し、

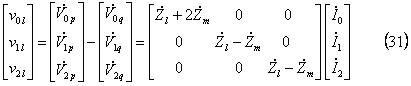
上式が（２０）式と同内容であることが確認できる。
　なお、（２０）式で、

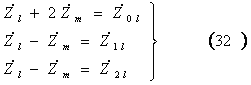
とおけば、（３３）式が成立する。

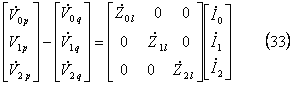
ここで、 、（ ）の関係にある。
この結果、三相線路の対称分回路は第８図となる。

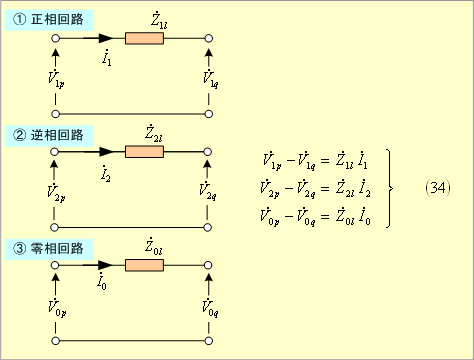
第８図　三相線路の対称分回路

なお、三相線路における対称分回路の性質を表す（３３）式は発電機の基本式（（５－３）式）で、

をに、をに、それぞれ置き換え、

とおくことで簡単に求めることもできる。

　ここで電源を含めた線路上のＱ点までの対称分計算式は、Ｐ点が発電機端と考えればよい。すなわち、（３３）式でＰ点の対称分電圧 を（５－３）式の発電機端子電圧 に置き換えればよいので、（３３）式は、

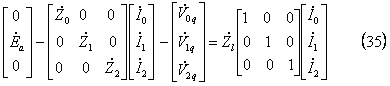
となる。この結果、Ｑ点での対称分電圧は

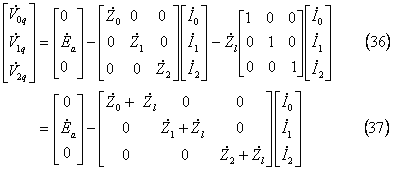
となる。
　このことは線路上のある点でも電源からその点までの零相、正相、逆相の各インピーダンスを とすれば、（５－３）式や（５）式の発電機の基本式の形がそのまま使用できることを意味している。このため改めて式を提示しておく。

～終わり～
■ぜひアンケートにご協力下さい■