〜終わり〜
■ぜひアンケートにご協力下さい■


(1) 直接接地方式
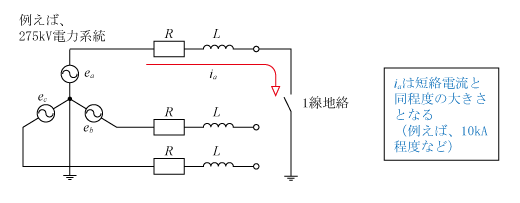
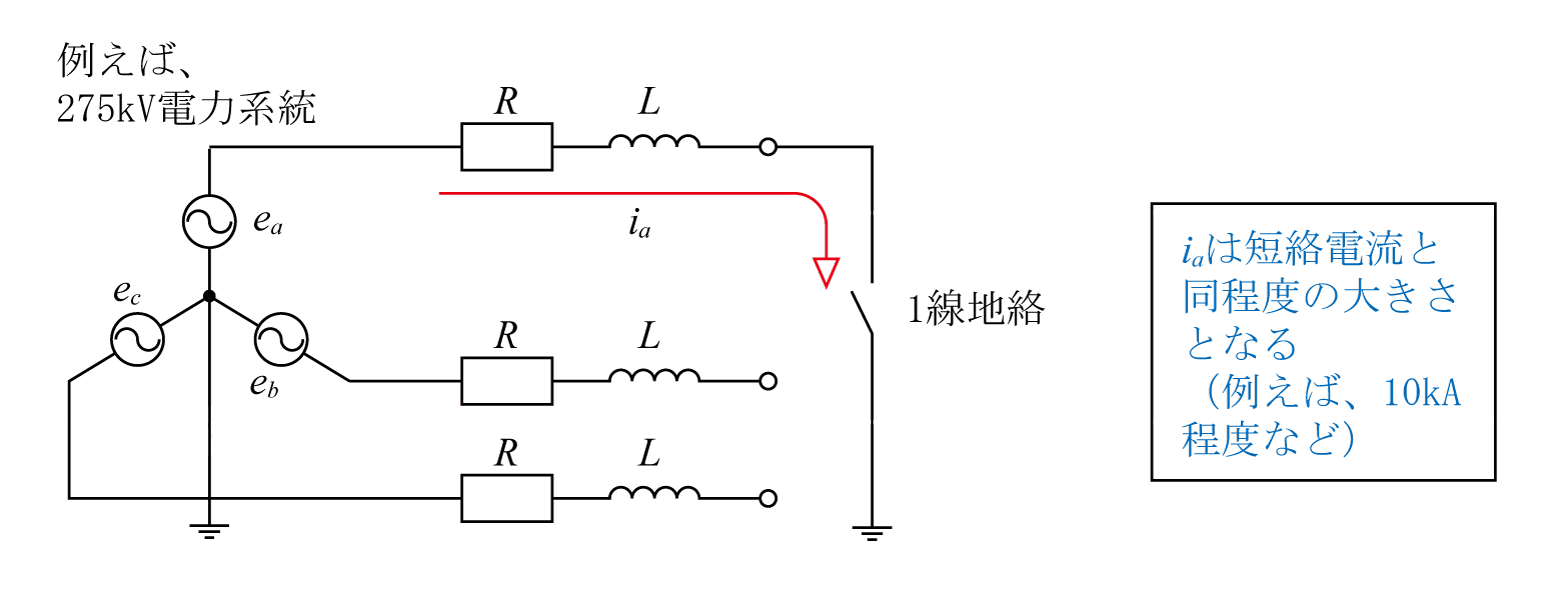
直接接地方式は220、275、500kVなどの超高圧系統で採用されている。第1図に示すように「中性点を直接に接地する」もので、地絡事故時(1線地絡事故時)は大きな地絡事故電流が流れる。この正確な大きさは「対称座標法によるインピーダンス(正相インピーダンスや零相インピーダンス)」を用いて示す必要があるが、ここでは簡単な方法で説明している。すなわち、「正相インピーダンス=零相インピーダンス」とすると、「地絡電流の大きさ=短絡電流の大きさ」になることを利用して波形を示している。
(2) 高抵抗接地方式
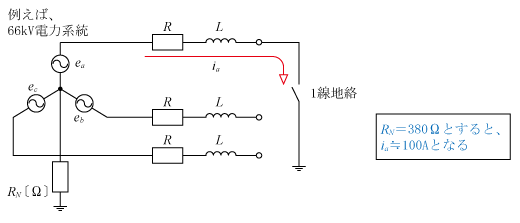
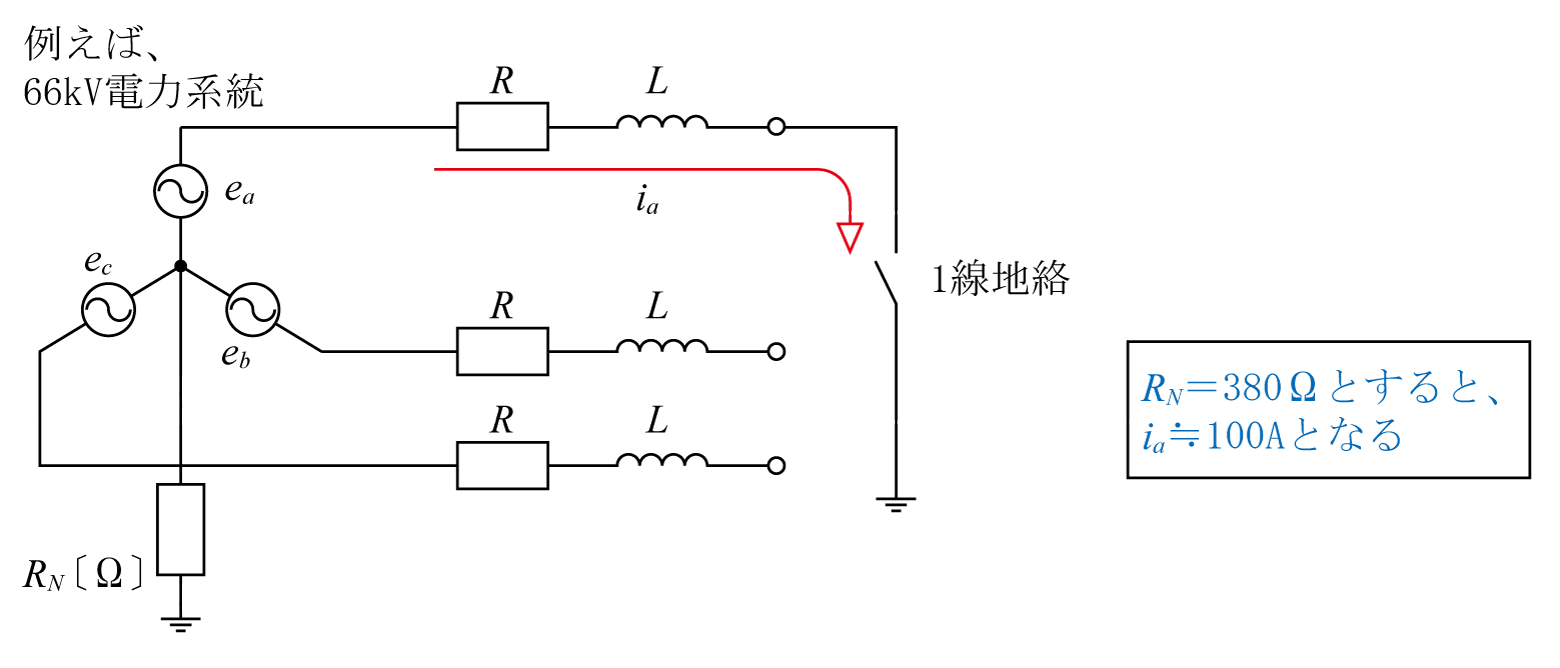
高抵抗接地方式は66、154kVなどの電力系統で採用されている。第2図に示すように「抵抗(図ではRN〔Ω〕)を介して中性点を接地する」もので、地絡事故電流(1線地絡事故時)はおおむねRNによって決まる。
このRNが例えば66kV系統で380Ω(RN =380Ω)とすると、1線地絡事故電流は100A程度(
![]()
![]() )となる。
)となる。
この場合も「対称座標法によるインピーダンス」を用いて示す必要があるが、中性点抵抗の値が線路インピーダンスなどに比べて十分大きいので、上記のように簡略して取り扱うことが多い。
(3) 非接地方式
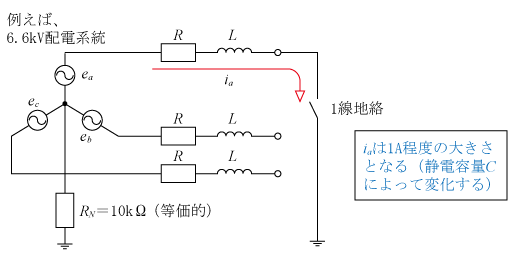
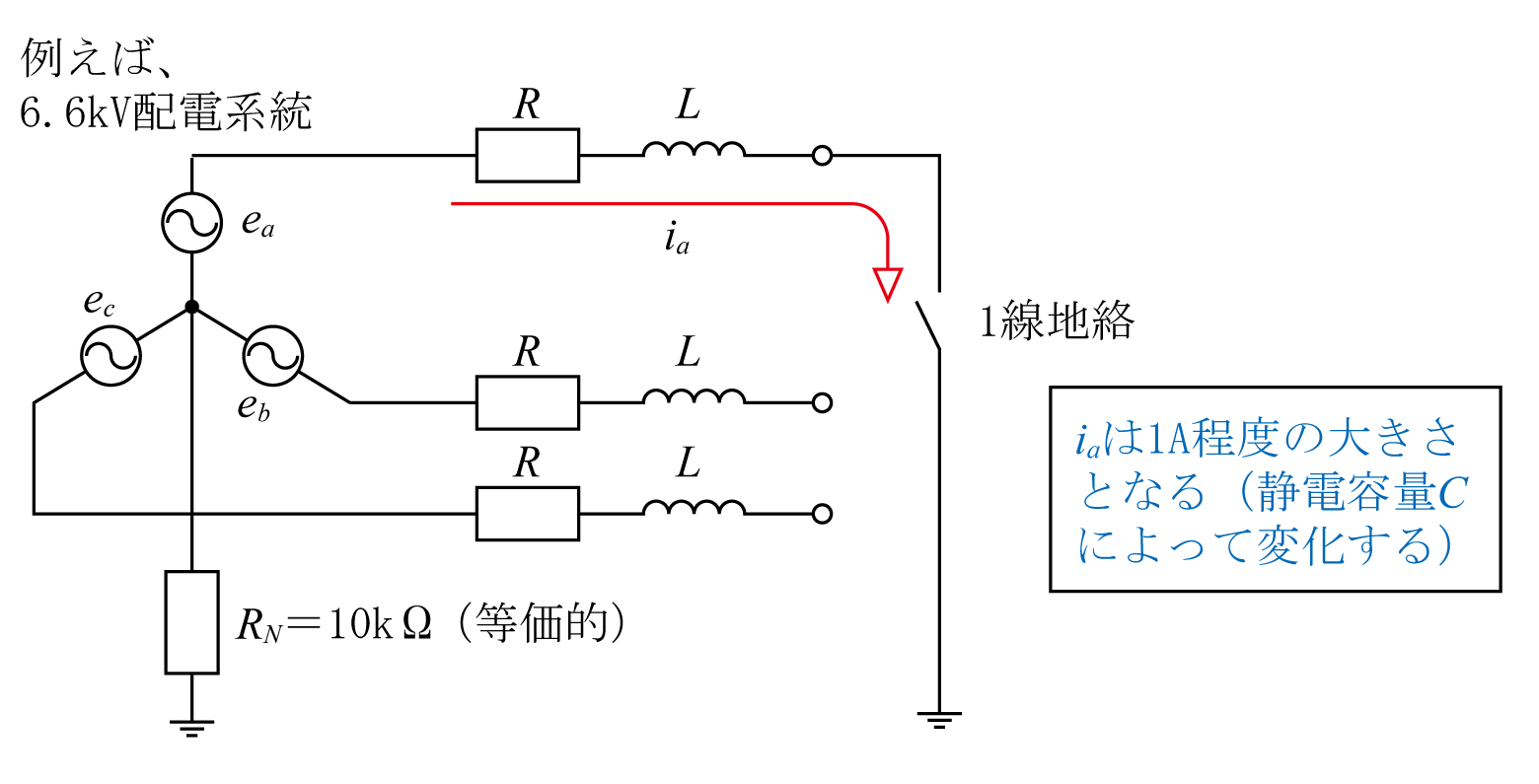
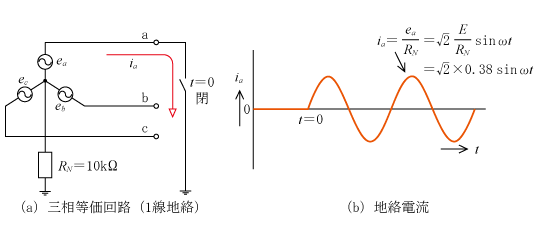
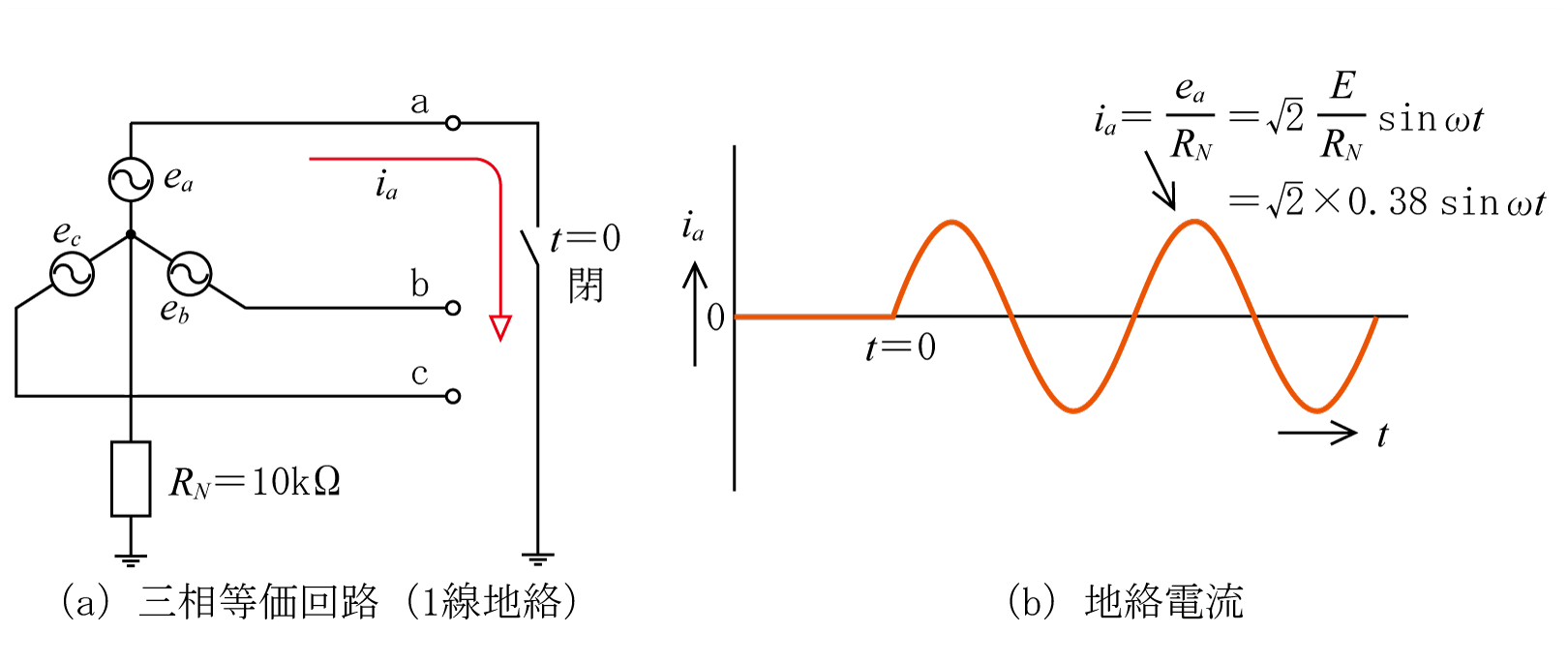
非接地方式は6.6kV配電系統などで採用されている。第3図に示すように「高い抵抗(図ではRN=10kΩ)を介して等価的に中性点を接地する」もので、地絡事故電流(1線地絡事故時)は「RNによる電流と配電線の静電容量Cによる電流」によって決まる。
非接地方式の場合、配電線インピーダンス(R 、L)などは無視している。
「RNによる電流」は0.38A(
![]()
![]() )として簡単に求めることができる。「配電線の静電容量Cによる電流」は配電系統の大きさ、地中配電線の有無などによって大きく変化する。一般的には0.38Aより大きな値になることが多い(例えば数Aになる)。
)として簡単に求めることができる。「配電線の静電容量Cによる電流」は配電系統の大きさ、地中配電線の有無などによって大きく変化する。一般的には0.38Aより大きな値になることが多い(例えば数Aになる)。
(1) Rだけの回路(L、 Cや大地抵抗を無視している)
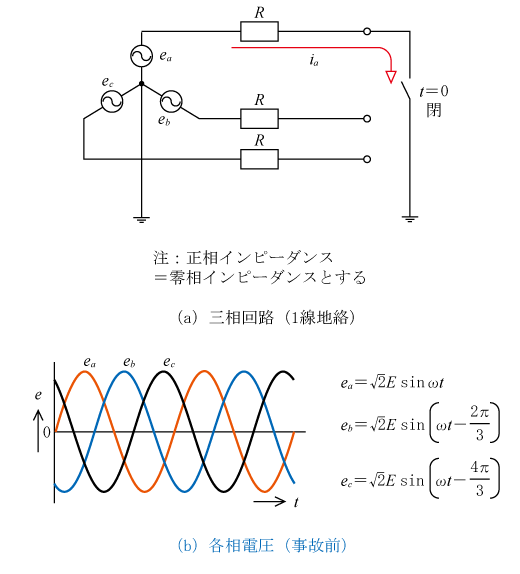
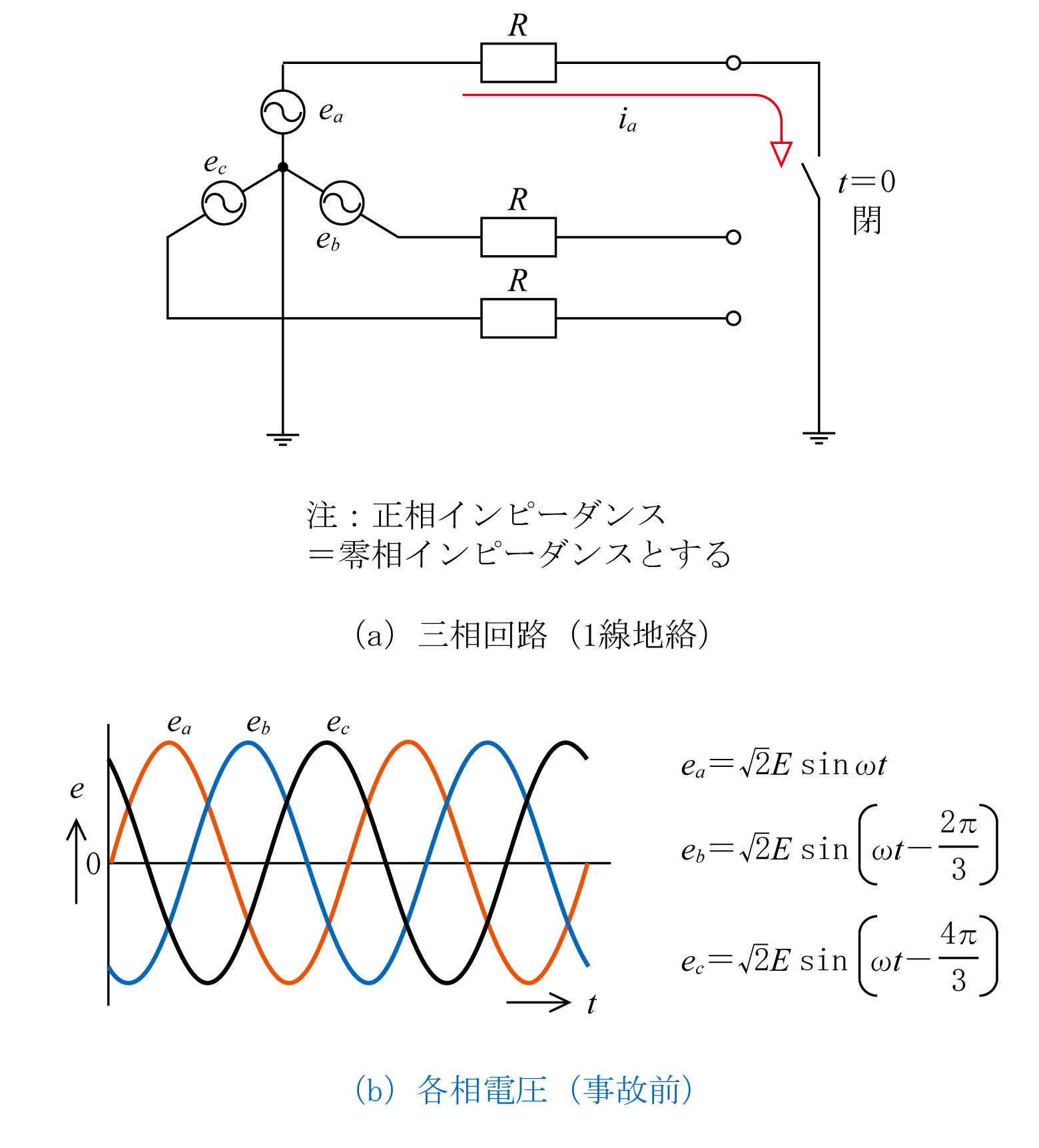
第4図に示すようにt=0秒の時点でa相で1線地絡事故が発生すると(同図(a)三相回路でa相でスイッチが開から閉になった状態になり)、1線地絡事故となり地絡電流が流れる。三相回路なので事故前の電圧は同図(b)のように120°位相差の電圧になる。
同図(a)はRのほかにL(インダクタンス)、C(キャパシタンス)、大地抵抗などあるが、ここでは簡単のためRだけで表している(すなわち、簡単のため「正相インピーダンス=零相インピーダンス」となるようにしている)。
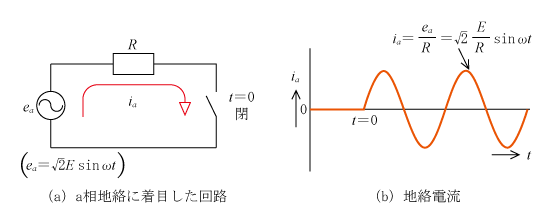
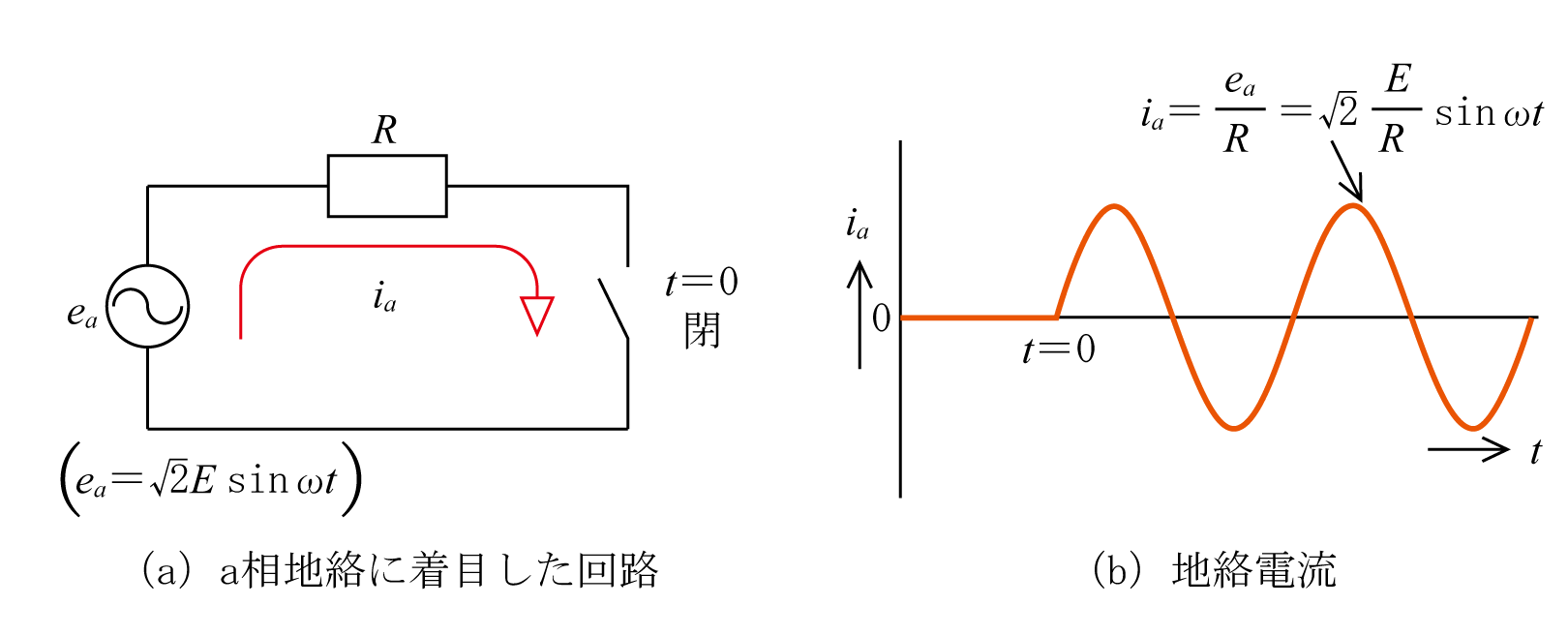
この場合の地絡電流は第5図に示すようになる。すなわち、第4図(a)の回路はa相の電源が抵抗Rを介して大地に接続された回路であるから、第5図(a)のようなeaを電源とした単相回路と考えることができる。したがって、同図(a)でt=0秒の時点でスイッチが開から閉になった状態で流れる電流が地絡事故電流となり、電流波形は同図(b)のような波形となる。
地絡事故時の事故相電圧は図示していないが、地絡事故点では0Vで、電源に近づくほど高くなり、電源端ではea〔V〕となる。
a相の電源電圧ea、地絡電流iaは(1)、(2)式となり、また、地絡電流の実効値Iは(3)式となる。
(2) R-L回路
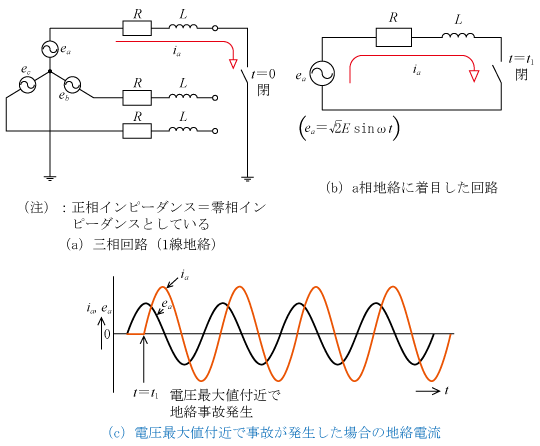
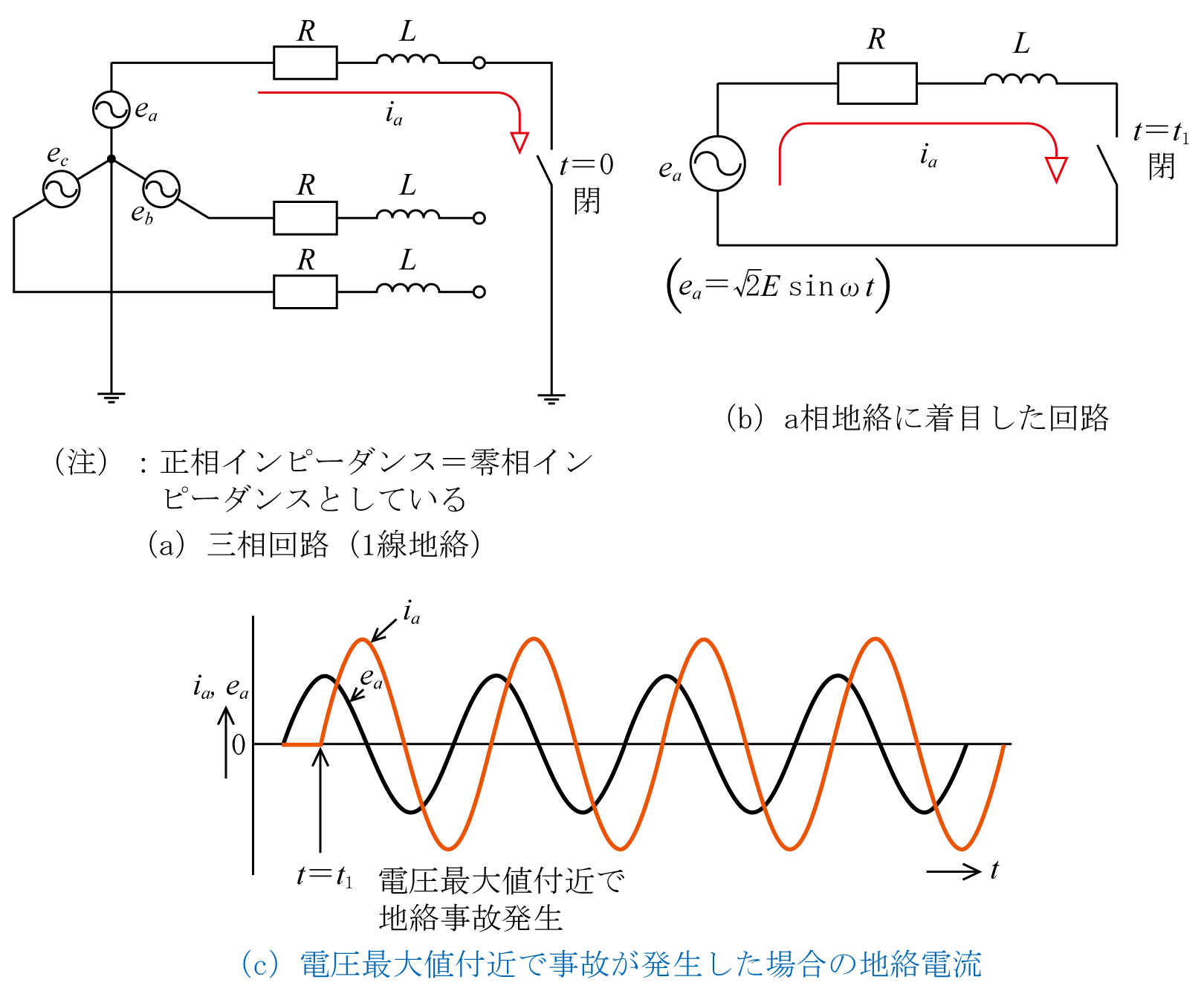
第6図に示すようにt=t1秒の時点でa相で1線地絡事故が発生すると(同図(a)三相回路でa相でスイッチが開から閉になった状態になり)、1線地絡事故となり地絡電流が流れる。前項では簡単のためRだけとしたが、ここではLも考慮していることが相違する。
この場合のa相地絡事故に着目した回路は、同図(b)となり、地絡電流波形は同図(c)のようになる。ただし、前回の「電圧・電流波形のいろいろ(4)(短絡事故)」で説明したように、R、L回路の電流は交流分に直流分が重畳し、直流分の大きさは事故発生時の電圧位相(タイミング)により変化するが、同図(c)は直流分がほぼ零となるタイミングで1線地絡事故が発生した場合を示している(ここでも正相インピーダンス=零相インピーダンスとして説明している)。
なお、この地絡電流iaを数式で示すと、(4)式のようになる。また、定常時の地絡電流は(6)式、実効値は(7)式となる(数式の導出過程は省略)。
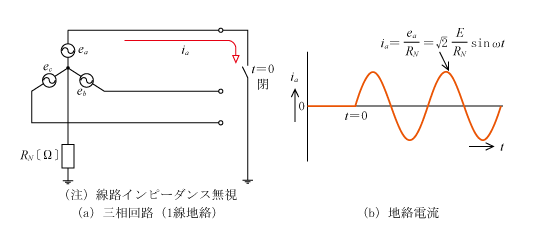
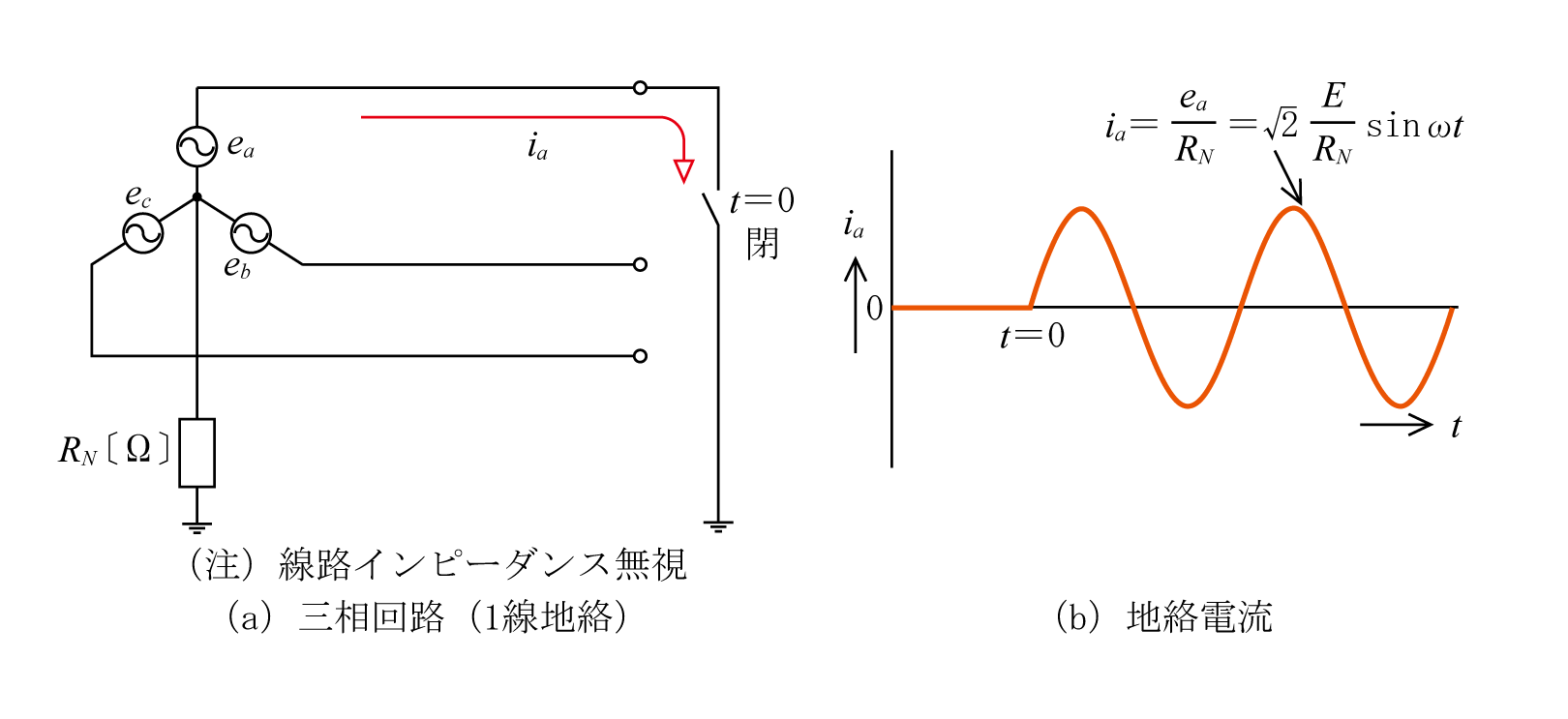
第7図に示すようにt=0秒の時点でa相で1線地絡事故が発生すると(同図(a)三相回路でa相でスイッチが開から閉になった状態になり)、1線地絡事故となり地絡電流が流れる。
同図(a)は中性点抵抗RNが線路インピーダンスに比べて大きいため、これを無視しRNだけの回路で表している。この回路から地絡電流は以下のとおりとなり、地絡電流の波形は同図(b)のようになる。
メモ:電源や送電線などのインピーダンスはおおむね数Ω程度である。例えば、66kV系統で短絡電流を少な目に見て10kAとしても、正相インピーダンスは数Ω以下(
![]()
![]() )となり、数百ΩのRNから見れば無視できる程度のものである。
)となり、数百ΩのRNから見れば無視できる程度のものである。
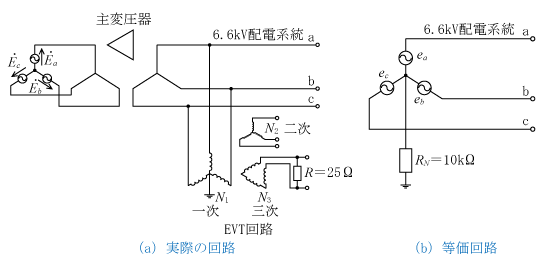
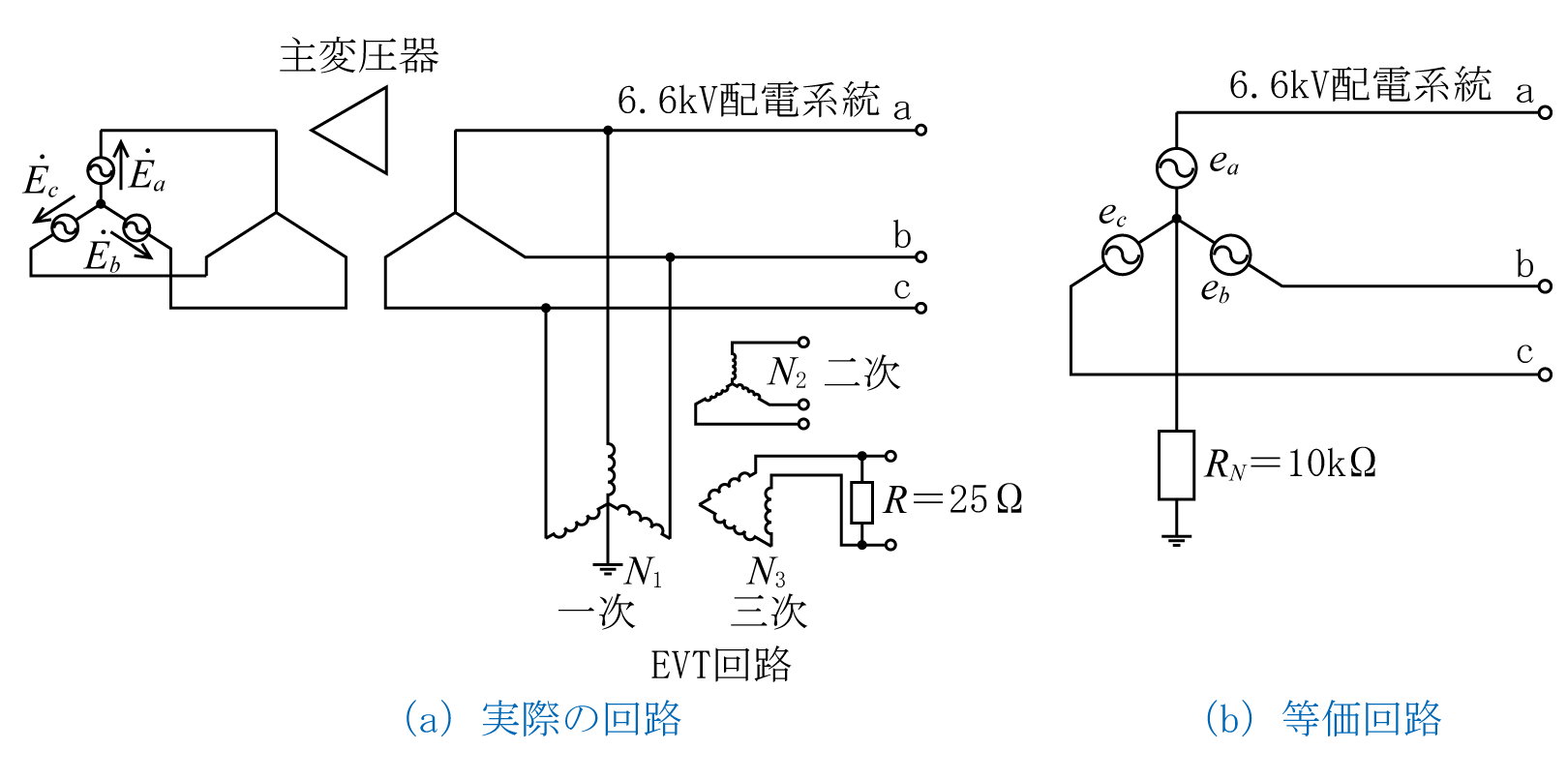
(1) 実際の回路と等価回路
6.6kV配電系統の実際の回路は第8図(a)に示すようになっており、6.6kV側にEVT回路が接続してあり、このEVT回路により中性点を等価的に高抵抗(例えば、RN =10kΩ)で接地しており、同図(b)のような等価回路となる。この場合も高抵抗接地方式と同様に線路インピーダンスは無視している。
ここで、EVTの三次側のΔ結線に接続された抵抗をR、EVTの一次と三次との変圧比をE1/E3=N1/N3とすると、RNは次式で表すことができる。
ここで、EVTの変圧比
![]()
![]() 、R=25Ωとすると、以下のとおりRN=10kΩとなる。
、R=25Ωとすると、以下のとおりRN=10kΩとなる。
(2) RNだけの場合
第9図に示すようにt=0秒の時点でa相で1線地絡事故が発生すると(同図(a)三相回路においてa相でスイッチが開から閉になった状態になり)、1線地絡事故となり地絡電流が流れる。
同図(a)は高抵抗接地方式と同様に中性点抵抗RNが線路インピーダンスに比べて大きいため、これを無視しRNだけの回路で表している。この回路から地絡電流は以下のとおりとなり、地絡電流の波形は同図(b)のようになる。
なお、数式で地絡電流を表すと、(11)、(12)式となる。(12)式の計算値は6.6kV系統でRN=10kΩの場合である。
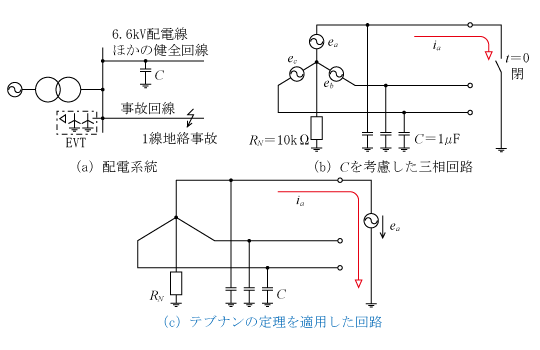
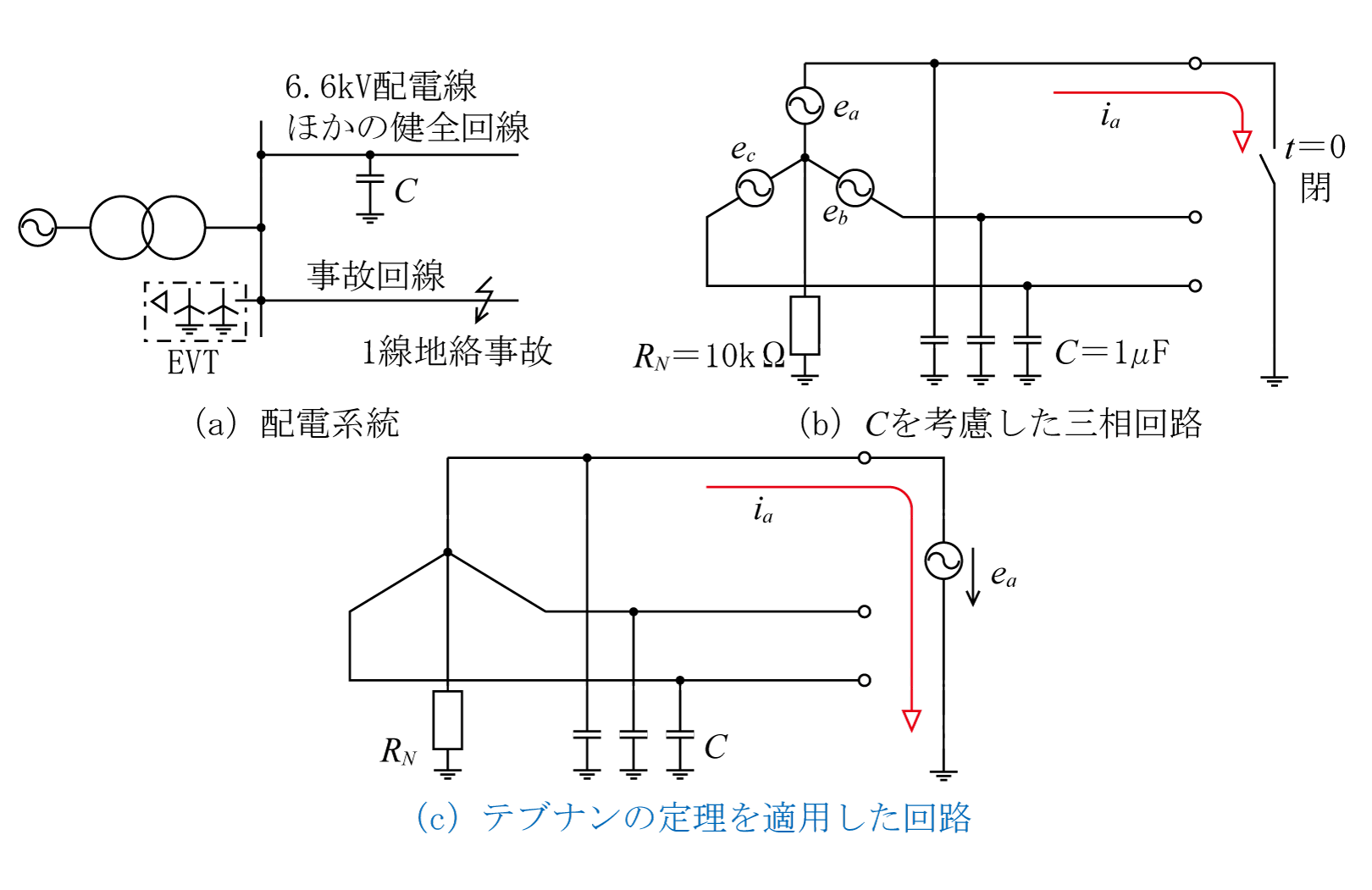
(3) 配電線の静電容量Cを考慮した場合
第10図に配電線の静電容量Cを考慮した場合の回路を示す。同図(a)のような配電系統で1線地絡事故が発生した場合の等価回路は同図(b)となる。このときの地絡電流を求める回路はテブナンの定理を用いると同図(c)となる。
第10図(c)の回路から、電流
![]()
![]() (ベクトル)は次式となる。
(ベクトル)は次式となる。
(14)式を瞬時値で表すと、(15)式となる。
例えば、RN=10kΩ、C=1.0μFとすると、
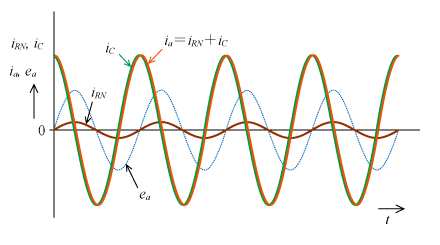
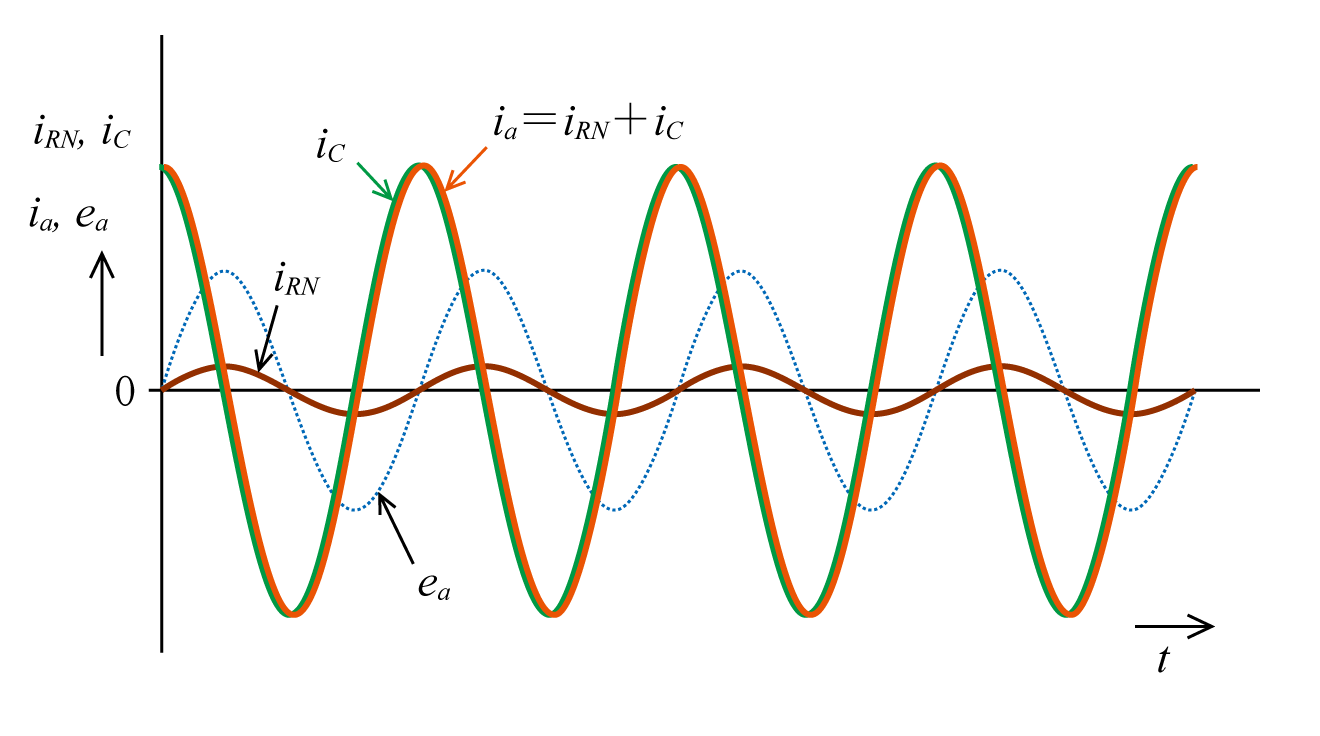
となり、Cによる電流は約3.6Aとなる。したがって、RNを流れる電流(0.38A)より1桁程度大きな電流が流れることになる。波形で示すと第11図となる。同図ではCに流れる電流位相が90°あるため、a相電圧eaも倍率を変えて参考として示しておいた。
中性点直接接地方式、高抵抗接地方式、非接地方式におけるそれぞれの地絡事故電流を簡単に示すのは大変無理がありますが、ここでは承知のうえで取り組んでみました。特に直接接地系統の地絡事故電流について、正相インピーダンス=零相インピーダンスとするなど荒っぽい説明になりましたが、概略の大きさや波形の状況をつかんでいただければと願っています。
(残念ですが、「対称座標法による直接接地系統の1線地絡事故電流など」の説明は紙面の都合上省略しました。また、短絡電流計算などでよく用いられる%Z法(パーセントインピーダンス法)についても同様に省略しています。)