〜終わり〜
■ぜひアンケートにご協力下さい■
電気理論や電力などの計算問題は､電気工学の法則の意味を理解し､幅広く数学の知識を応用して解かなければならないが、試験会場ではあまり時間をかけることはできないため、方針を素早く決定し要領よく計算する必要がある。しかし、その方針次第で落とし穴にはまり、誤答したり時間がかかって解答が求まらないことがある。このシリーズでは、このような落とし穴の例をいくつか取り上げ、計算運用の上手なテクニックを学ぶ。今回は、オームの法則および電位降下法による抵抗測定誤差について解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
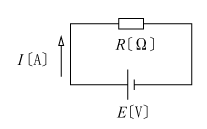
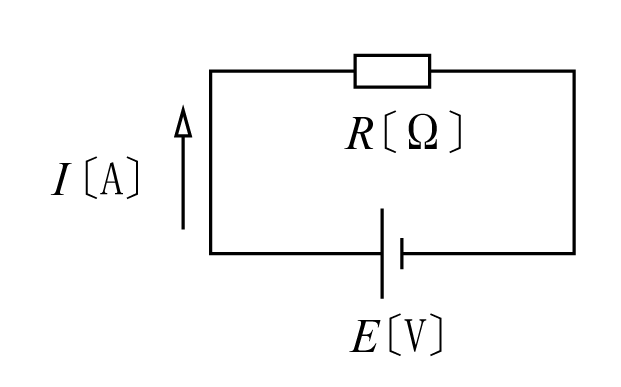
〔例題1〕 第1図に示す回路で、もし抵抗値を20％減らしたとすれば、電流は何％増えるだろうか。
■太郎君の答 オームの法則に従えば、E=I・RでEは一定であるから、Rが20％減れば、Iは20％増えることになる。
■次郎君の答 はじめの電流はI=E/Rだから、Rを20％減らすと、
したがって、電流は5倍になる。
■三郎君の答 I=E/Rで、R=1、E=1とすると、
したがって、電流は1.25倍になる。
「オームの法則の式を当てはめるだけだから簡単」とうっかりすると、このような不完全な答を出してしまう。3人のどこに間違いがあるだろうか。
■太郎君の場合 E=I・RでRが20％減れば、Iは20％増すだろうと考えるのは、いかにも当然のようであるが、そうはいかない。計算式の取扱いで積と和を混同しないよう注意が必要である。2数の和の場合には片方が減った分、片方を増やせば一定であるが、積の場合はそうならない。
■次郎君の場合 20％減らした分を0.2Rとしてはいけない。残りは0.8Rである。
■三郎君の場合 答は正しいが、解答の仕方が自分で勝手に決めた数値を使ってはよくない。RやEの数値は与えられていないので、ぜひ文字を使って考える習慣をつけないと、今後の応用問題に対処できなくなる。正しくは次のように式を展開して下さい。
〔正解〕 I=E/Rで、Rを20％減らすと残りの抵抗は、R−0.2R=0.8Rとなる。したがって、減らした後の電流Iは、
電流は1.25倍となる。
〔例題2〕 2kWの電熱器具で、100V用と200V用の2種類がある。この2種類の電熱器具を、それぞれ100Vのコンセントに接続して、同じ量の水を沸かしたとすると、どちらが早く沸くであろうか。
■太郎君の答 どちらも2kWの電熱器具であるから、同じ量の水であれば同時に沸騰する。
■次郎君の答 100V用よりも200V用の電熱器具のほうが電圧が倍あるので半分の時間で沸騰する。
■三郎君の答 200V用の電熱器具を100Vのコンセントにつないだ場合、電圧が半分であるから、電熱器具の容量も半分の1kWとなるものと考えられる。そのため200V用のほうが時間が倍かかることになる。
ここに載せた3人の答は、もっともらしく答えているが、いずれも間違っている。皆さんの中にもこのような間違いをする人はいないだろうか。正しくは電力の式の意味を理解し、次のように答えなければならない。
〔解説と正解〕
100V用の電熱器具のニクロム線の抵抗Rは、
一方、200V用の電熱器具の抵抗Rは、
このように二つの電熱器具のもつ抵抗値がいくらあるかを最初に求めることが大切で、この抵抗値をもつ電熱器具を100Vのコンセントにつないだとき、それぞれの電力がどうなるかを考えなければならない。
200V用と100V用の2kWという言葉だけにとらわれてはいけない。
100V用の電熱器具を100Vのコンセントにつないだときの電流Iは、I=100/5=20Aであるから、電力Pは、
P=VI=100×20=2,000W
となるが、200V用の電熱器具を100Vのコンセントにつないだときの電流Iは、
I=100/20=5Aであるから、電力Pは、
P=VI=100×5=500W
となる。
この結果から200V用のほうは、実際は500Wしか電力を消費しないことになり、同量の水を沸かした場合、4倍の時間がかかることになる。ちょっと意外な結果である。
〔例題3〕 太郎君と次郎君がそれぞれ電圧計と電流計を使って未知抵抗Rの値を測定した。2人の使った電圧計、電流計はいずれも同じもので、内部抵抗が電圧計3kΩ、電流計4.1Ωのものであり、2人は次のような測定結果を得た。
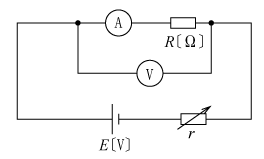
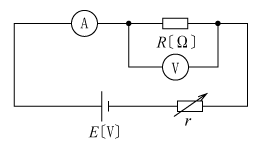
ただし、太郎君は第2図の回路で、電圧計Vの振れが2Vになるようにrを調整したところ、電流計の指示は1.95mAであった。
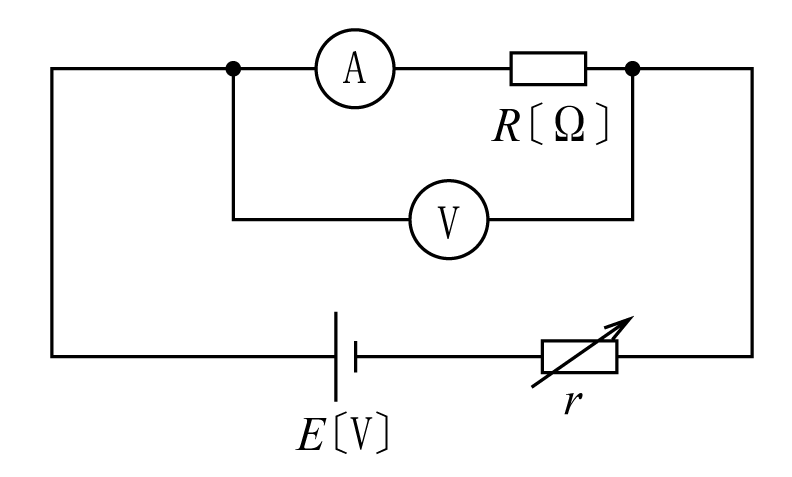
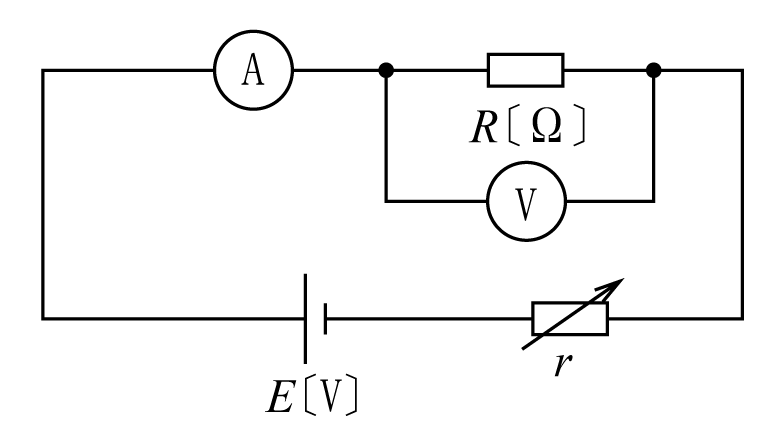
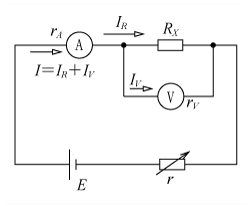
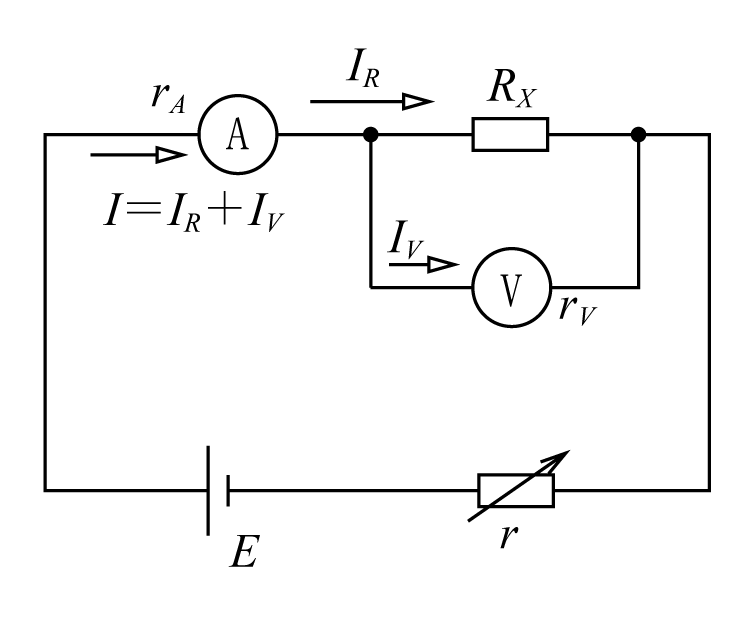
また、次郎君は第3図の回路で、太郎君と同様に電圧計Vの振れを2Vにしたところ、電流計の読みは2.64mAであった。測定を繰り返しても同じ結果が出た。
さて、回路が異なる二人の測定値には大きな開きが出てしまったが、それぞれ自分の値が正しいと言っている。あなたはどう思うか。
この実験のデータから未知抵抗Rは、
で求めることができる。
そこで、二人の計算結果を示すと次のようになった。
■太郎君の未知抵抗Rの計算
■次郎君の未知抵抗Rの計算
計算を繰り返しても結果は同じで、二人の測定結果には、実に268Ωもの大きな差が出ました。これはどうしたことであろうか。
電流計、電圧計を用いて抵抗を流れる電流と抵抗に加わる電圧を測定し、オームの法則によって未知抵抗の値を求める方法は電位降下法、あるいは電流計・電圧計法と呼ばれ、簡単に抵抗が測定できるのでよく用いられる。
しかし、第2図および第3図の回路で注意しなければならないのは、電流計、電圧計を入れたことによって、電流計、電圧計はそれぞれ正しく抵抗Rに流れる電流及び抵抗Rに加わる電圧を指示していなければならないはずである。ところが、この両方の回路はこの点でそれぞれ問題がありそうなので、以下に解説する。
〔解説〕 さて、第2図の太郎君の回路では、電流計は正しく未知抵抗Rに流れる電流IRを示すが、電圧計は未知抵抗Rに加わる電圧VRと、電流計に加わる電圧（電流計の内部抵抗rAとIRの積によるもの）VAの和を示す。このVAが誤差となって出てくることが分かると思う。
したがって、第2図の回路を使う場合には、未知抵抗Rが比較的大きい場合に用いると誤差の少ない測定ができる。
一方、第3図の次郎君の回路では、電圧計は正しく未知抵抗Rに加わる電圧を示すが、電流計の読みは未知抵抗Rに流れる電流IRと電圧計に流れる電流IV（電圧計の内部抵抗rvで電圧計の指示Vを割った値）との和になる。このIVが誤差になるので、IVに対してIRの比率が大きければ大きいほど誤差が小さくなる。
したがって、第3図の回路を使う場合は、未知抵抗Rが比較的小さい場合に用いると誤差の少ない測定ができることになる。
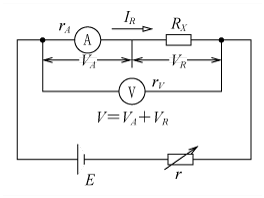
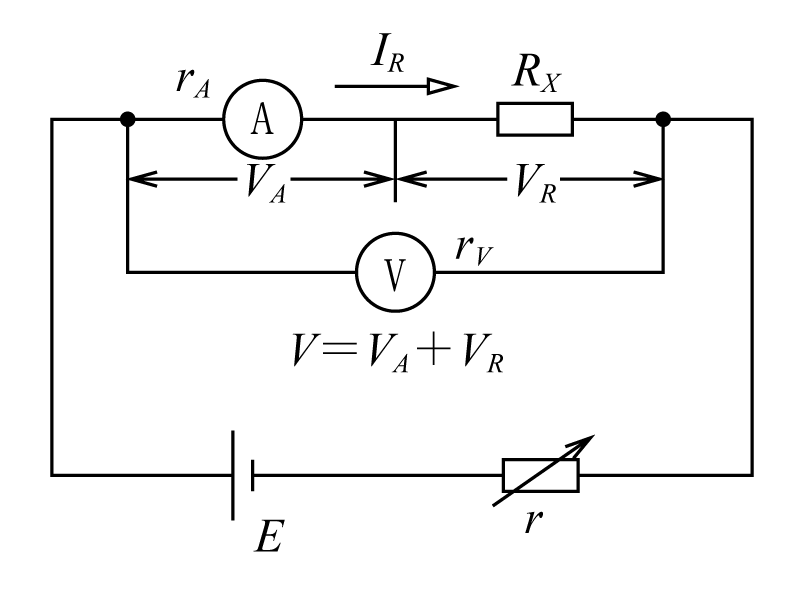
なお、太郎君、次郎君の採用した回路で、いずれも誤差を更に少なくするには電流計、電圧計のそれぞれの内部抵抗rA 、rvを求めて、第4図、第5図のようにRXの値を計算すればよいことが分かる。
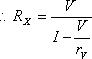
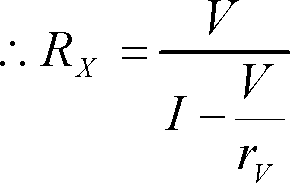
〔例題4〕 電位降下法により1kΩ程度の抵抗RをR=（電圧計の読み）/（電流計の読み）をもとに測定したい。電圧計と電流計の内部抵抗がそれぞれ3kΩ、4Ωとすれば、第4図、第5図のどちらの回路を使えばよいか考えてみよう。
〔解説〕 二つの回路図について、それぞれ検討してみる。第4図の結線でVR=IR RXに対して、VA=IR rAが誤差になるが、rAは4ΩでRXの1,000Ωに対してかなり小さいから誤差は小さい。
一方、第5図の結線ではIVが誤差になるが、RX=1kΩ、rV=3kΩであるから、
となってIVはIRの1/3の大きさをもつことになり、誤差は第4図の回路に比べて非常に大きくなる。したがって、この場合は第4図の結線を行えば誤差は小さくできることになる。