第1回で述べたように、『鎖交磁束が時間と共に変化し、コイル（回路）に起電力が発生する現象』を電磁誘導現象という。このとき発生する起電力（誘導起電力）は、ファラデーの法則によって、

誘導起電力の大きさは、磁束鎖交数（巻数×鎖交磁束）の時間的変化に比例する。

　である。ここで、磁束鎖交数Ψ、巻数n、鎖交磁束Φ、時間t、比例定数Kとすれば、起電力eは、

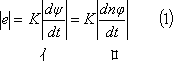
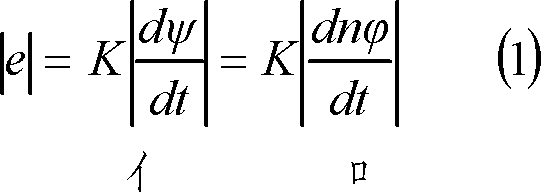
と、定性式で表される。上式で、単位を鎖交磁束Φ[Wb]、時間t[s]とすれば、

となり定量的に式表示できる。

　つまり、

誘導起電力の大きさは、磁束鎖交数（巻数×鎖交磁束）の時間的変化率に等しい。

　私たちが遭遇する電磁誘導は、殆どの場合が、「電流がつくる磁束によって起こる電磁誘導現象」である。したがって、一般に、磁束は電流に比例しているので、電磁誘導現象を起こす程度を、

と数値化して表現する。インダクタンスの単位は、[Wb/A]であるが、これを以後新しい単位記号[H](ヘンリー)を使用する。

　電磁誘導現象には発生形態によって第1図のように二つのタイプがある。同図（a）のように、あるコイルに外部から流入した電流がつくる磁束によって、自コイルに起こる電磁誘導現象を自己誘導作用という。この時のインダクタンスを自己インダクタンスといい、次式のLで示される。

　Lは、コイルの形状、巻数、媒質などによって決まるコイル固有の値である。

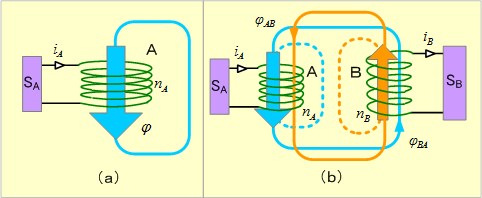
第1図　インダクタンスの種類

　また、同図（b）のように、回路A（B）に流れる電流がつくる磁束の一部が他回路B（A）と鎖交するために起こる電磁誘導現象を相互誘導作用という。この時のインダクタンスを相互インダクタンスといい、次式のMで示される。

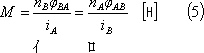
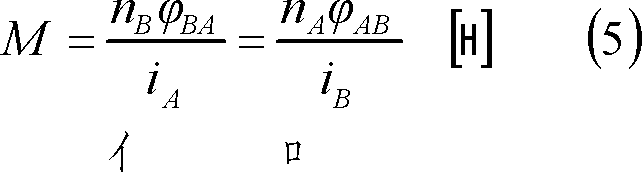
　Mは、コイルの形状、巻数、媒質などのほか、両コイルの相対的位置関係によって決まる値である。

　第2図に示す自己インダクタンスL[H]のコイルにおいて、電流i[A]、巻数n、鎖交磁束 [Wb]であるとき、自己誘導作用によりコイルに誘導される起電力eは、図のように「電流iの正方向と同じ方向を起電力の正方向に合わせる」と、次のようにして求められる。

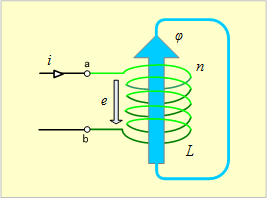
第2図　自己インダクタンスに発生する誘導起電力

　（4）式より、

の関係にあるので、eは次式となる。

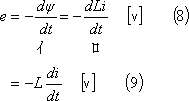
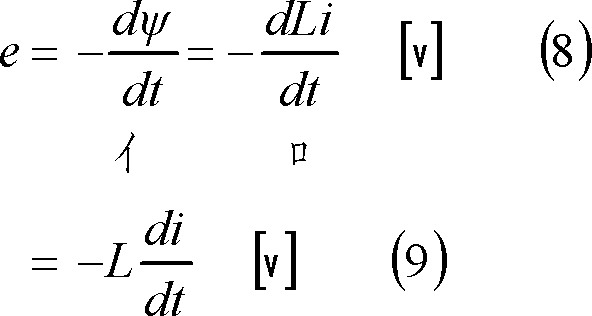
　したがって、上式より、自己インダクタンスL[H]のコイルとは、『そのコイルに単位電流変化（1[A／s]）を与えたとき、誘導される起電力がL[V]である』ことを意味している。

　（1）　自己インダクタンスに流す電流によってどんな起電力が誘導されるが調べてみよう。

　第3図に示すL[H]のコイルにおいて、グラフに示す電流i₁、i₂を流すと、誘導起電力eは正方向を図のように電流と同じ方向（a端子からb端子へ向かう方向）に選べば、eはどんなグラフになるだろうか。

第3図　Lにはどんな起電力が誘導されるか?

　①　図中の再生ボタンイを押して、電流i₁によって起電力（e₁）がどのように誘導されるか観察してみよう。観察が終了したら戻りボタンハを押して初期状態に戻す。

　②　今度は電流i₂について、再生ボタンロを押して、①と同様な観察をする。

　観察の結果、起電力は第4図のように誘導されたことが確認できる。

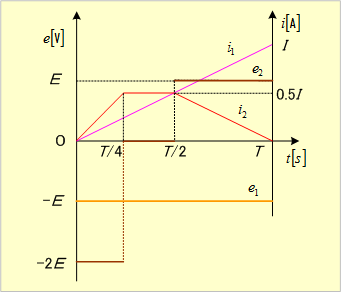
第4図　実験①②の誘導起電力波形

　起電力e₁は、

　0T区間では、　

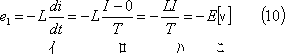
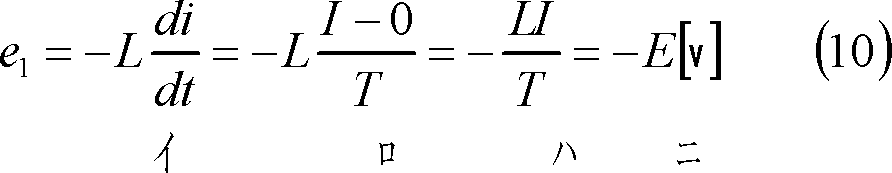
　起電力e₂は、

　0〜T／4区間では、　　　

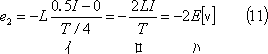
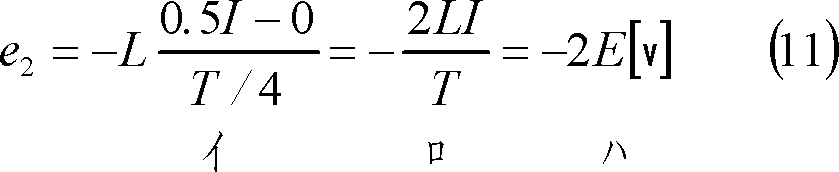
　T／4〜T／2区間では、　

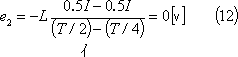
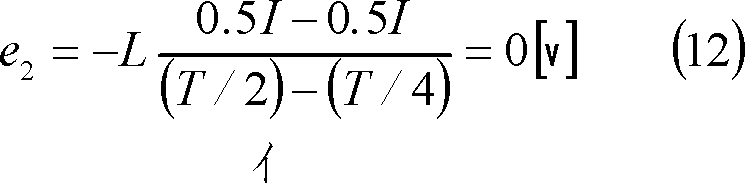
　T／2〜T区間では、　　　

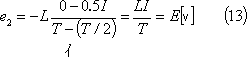
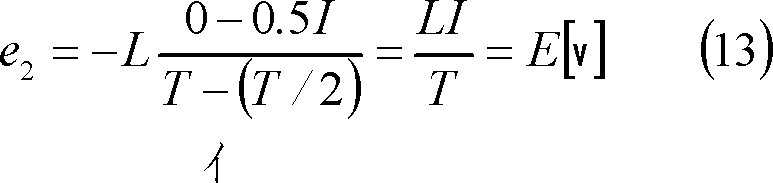
　（2）　次に第6図に示すL[H]のコイルに正弦波交流電流iを流すと、どんな起電力が誘導されるか調べてみよう。

　Lに誘導される起電力（誘導起電力）eは、電池の起電力などとは異なり、それ自身では起電力を保有していない。つまり、抵抗に電流が流れて抵抗端に現れる電圧（電圧降下）と同じように、コイルに外部から電流が流れ込んではじめて現れる起電力（電圧）なので、電気回路上では、抵抗の電圧降下と同じように扱うことが望ましい。したがって、これまでは第5図（b）のように扱ってきたが、以後は同図（a）の抵抗にならって同図（c）のように、Lに誘導される起電力は、その正の方向を電流と逆の方向としたL端電圧v_Lとして扱うことが多い。したがって、eとの関係は（14）式であり、v_Lの式は(15)式となる。

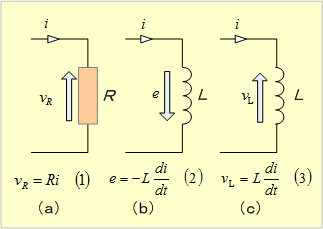
第5図

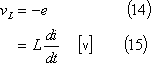
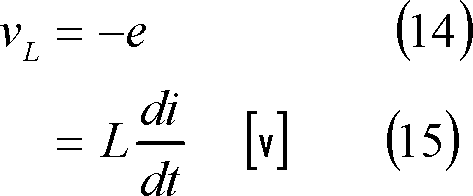
第6図　Lに正弦波交流電流を流すと、どんな電圧が現れるか?

　では、第6図でL端に現れる電圧を観察してみよう。

　（3）　イの再生ボタン>を押して電流iによってコイルと鎖交する磁束 のグラフと、コイルに鎖交する磁束 の様子を観察してみよう。観察が終了したら戻るボタンハを押して初期画面へ戻る。

　観察の結果、 は右手親指の法則によって、iによって上向きにでき、この方向を磁束の正方向にとれば、図のように電流と同相の波形となることが確認できる。

　（4）　次に、この磁束がコイルと鎖交することによってできる誘導起電力を図の方向のL端電圧v_Lとしてみたとき、この電圧波形がどうなるか、ロの再生ボタン>を押して観察してみよう。観察が終わり、各波形間の関係が確認できたら戻るボタンハを押して初期画面に戻る。

　画面中央の上段の窓には、各瞬間のiの接線勾配が示されている。v_Lは（15）式からiの接線勾配に比例するので、この勾配線に連動してv_Lが変化する様子がよく観察できる。

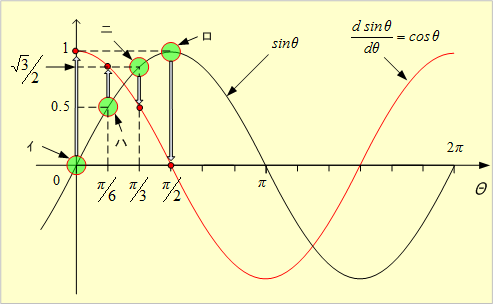
第7図　正弦波交流の勾配

　iの接線勾配は、実質的には正弦波の接線勾配であり、第7図において、各角度における接線勾配は、図のように、イ点では1、ロ点では零、ハ点では 、ニ点では0．5、となり、全体的には｢sinθのθに対する接線勾配はcosθのグラフで示される」ことがわかる。

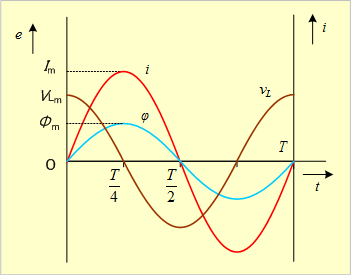
第8図　正弦波交流電流でコイルに現れる電圧

　これらを式で示すと、次のようになる。

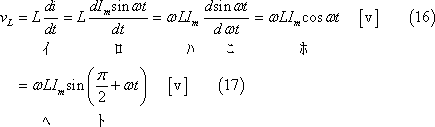
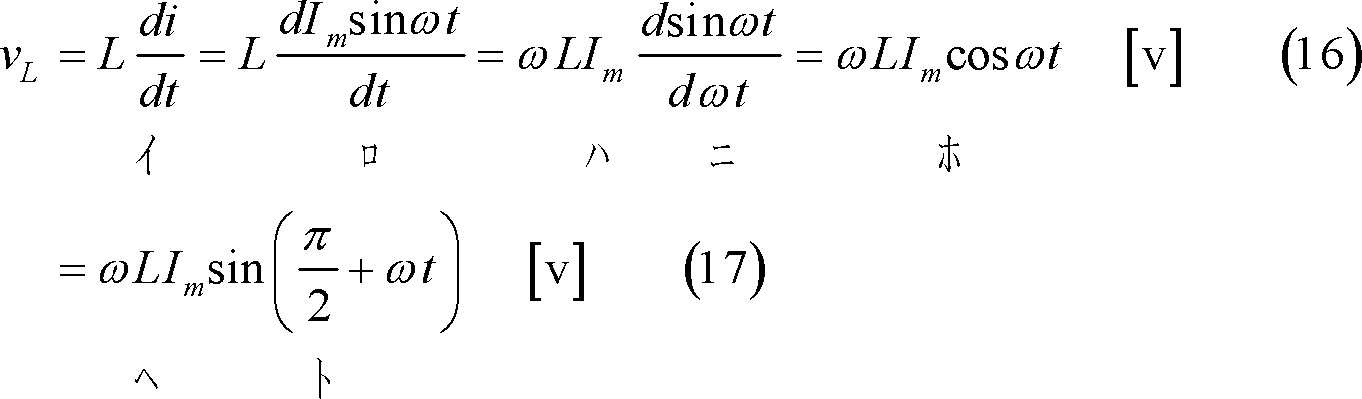
　上式より、

Lの端子電圧は、最大値V_Lmが （実効値V= ）で、電流より90°位相の進んだ電圧である。

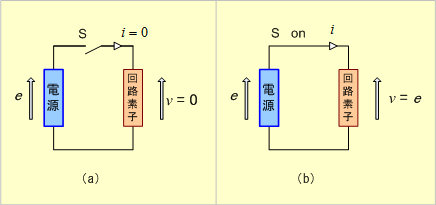
第9図　電源の起電力と回路素子の端子電圧の関係

　一般的に電気回路は第9図（a）のように起電力と回路素子とで構成されており、同図（b）のように起電力が回路素子に印加されると電流が流れはじめ、充分時間が経過すると、電流は一定値に落ち着くか、一定の周期的変化に移行する。この状態（定常状態）では電源の起電力と回路素子の端子電圧とは常に等しい。換言すれば、回路素子電圧が起電力に等しくなるような電流が回路を流れるわけであり、回路素子端の電圧は起電力を表しているわけである。つまり、第8図で示した素子端の電圧v_Lは起電力でもあるわけである。

　以上のことから、

実効値Vの交流電圧eを、自己インダクタンスLに印加すると、実効値IがV／ωLの交流電流iがeより90º遅れた位相で流れる。

という性質がある。　

　電磁誘導現象の内容は理解しづらい面があるのは誰もが認めるところ。しかし、私たちの身の回りを見ると、この現象とよく似た現象がある。それは、物体の運動で、第1表は、物体の運動と電磁誘導現象を対比したものである。

第1表　　物体の運動と電磁誘導現象の対比

	物体の運動	電磁誘導現象
１　関係式
２　関係対応量A	力　f [N]	起電力　e [V]
３　関係対応量B	質量　m [kg]	自己インダクタンス L [H]
４　関係対応量C	速度　v [m/s]	電流　i [C/s]
５　関係対応量D	時間　t [s]

　力学の運動方程式は、「物体に速度の変化を与えると、物体は力を受ける」という性質を定量表現したもので、私達は日常よく体験する現象である。

　例えば、電車や自動車に乗って第10図（a）に示す速度変化を受けると、われわれの身体はいろいろな力を感じる。これが、運動法則にともなう力である。

　①　AB間のような一定な加速（速度の変化率 が一定）を受けると、第1表の運動方程式の関係を満足するような力が働く。つまり、一定な力を運動方向と反対の方向に受ける。

　②　BC間のように定速走行の場合は力を受けない。（ ）

　③　また、ブレーキが掛かり、速度が次第に減少して行くとき、図のように減速の度合い（ ）が一定であれば、われわれは第1表の方程式で決まる一定な力を、運動方向と同じ方向に受ける、という具合に日常体験しているわけである。

　電磁誘導現象も物理的内容は異なるにせよ、表からわかるように、時間に関する変化は物体の運動と全く同じであると云える。つまり、電気回路において、何らかの原因で電流が時間と共に増加すると、（9）式で決まる起電力が発生し、 の大きさの起電力が、電流の方向と逆方向（e<0）にできる。また、その逆に電流が時間と共に減少する場合は、（9）式で決まる起電力が、つまり、 の起電力が、電流の方向と同方向（e>0）に発生するということである。もちろん、電流に変動がない場合（ ）は、起電力は発生しない。

　それでは、第3図の②のケースについて運動と比べてみると第10図となる。

　このように電磁誘導現象は、力学の運動法則に類推して捉えると、イメージしやすいので、大いに活用していただきたい。

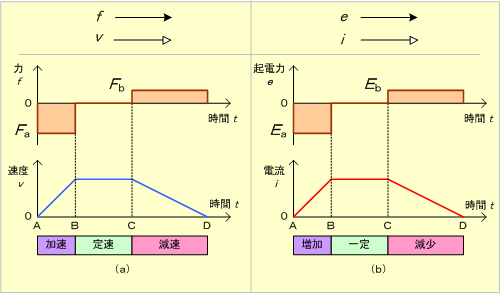
第10図　物体の運動と電磁誘導現象を比べてみると

　（1）インダクタンスの定義・・・・・・（3）式

　（2）インダクタンスの種類・・・・・・　第1図

　（3）自己インダクタンスの電流と端子電圧の関係（大きさと方向）・・・・・・（9）,（15）式、第5図

　（4）交流回路における電流と端子電圧の関係（大きさと位相）・・・・・・第8図、（17）式、ほか。