〜終わり〜
■ぜひアンケートにご協力下さい■


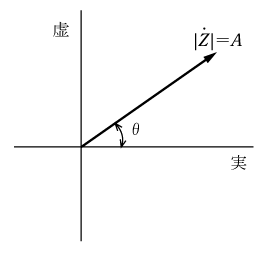
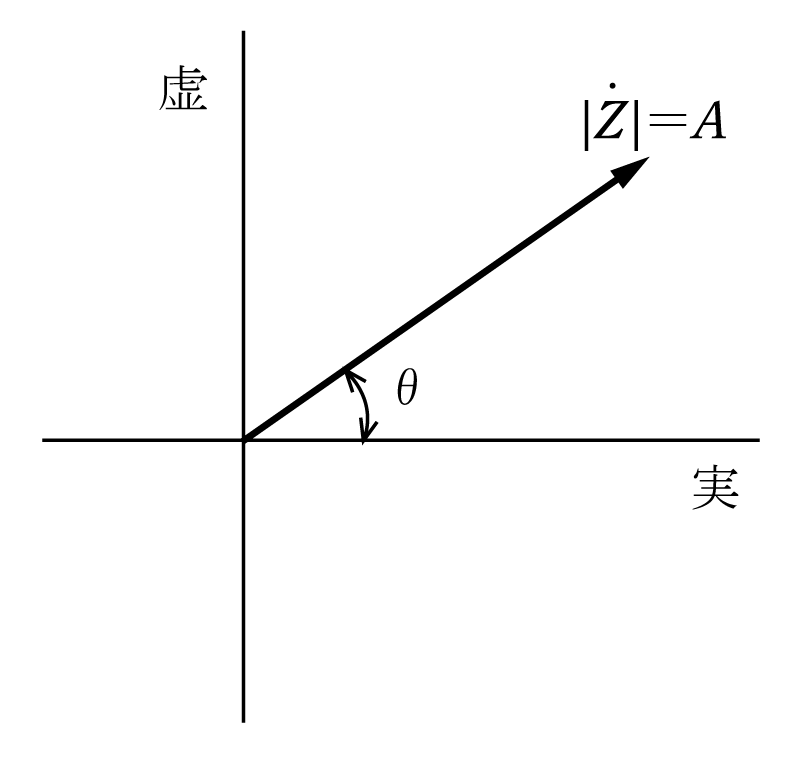
第1図のように大きさAの実数軸上にあるベクトルを位相角θだけ進めたいと思ったならば、Aに(cosθ+jsinθ)を掛ければよい。いいかえれば、大きさAで位相角θのベクトルZを複素数で表すと、
![]()
![]() ということになる。つまり、カッコ内の部分を利用すれば、ある大きさのベクトルを自由に位相を変えてやることができる。もし位相角をθ遅らせたい場合には(cosθ−jsinθ)を掛ければよいことになる。
ということになる。つまり、カッコ内の部分を利用すれば、ある大きさのベクトルを自由に位相を変えてやることができる。もし位相角をθ遅らせたい場合には(cosθ−jsinθ)を掛ければよいことになる。
電力計算のテクニックを学習する前に、(cosθ±jsinθ)がベクトルの位置を支配していることを知っておこう。
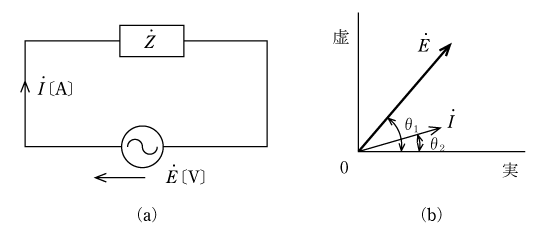
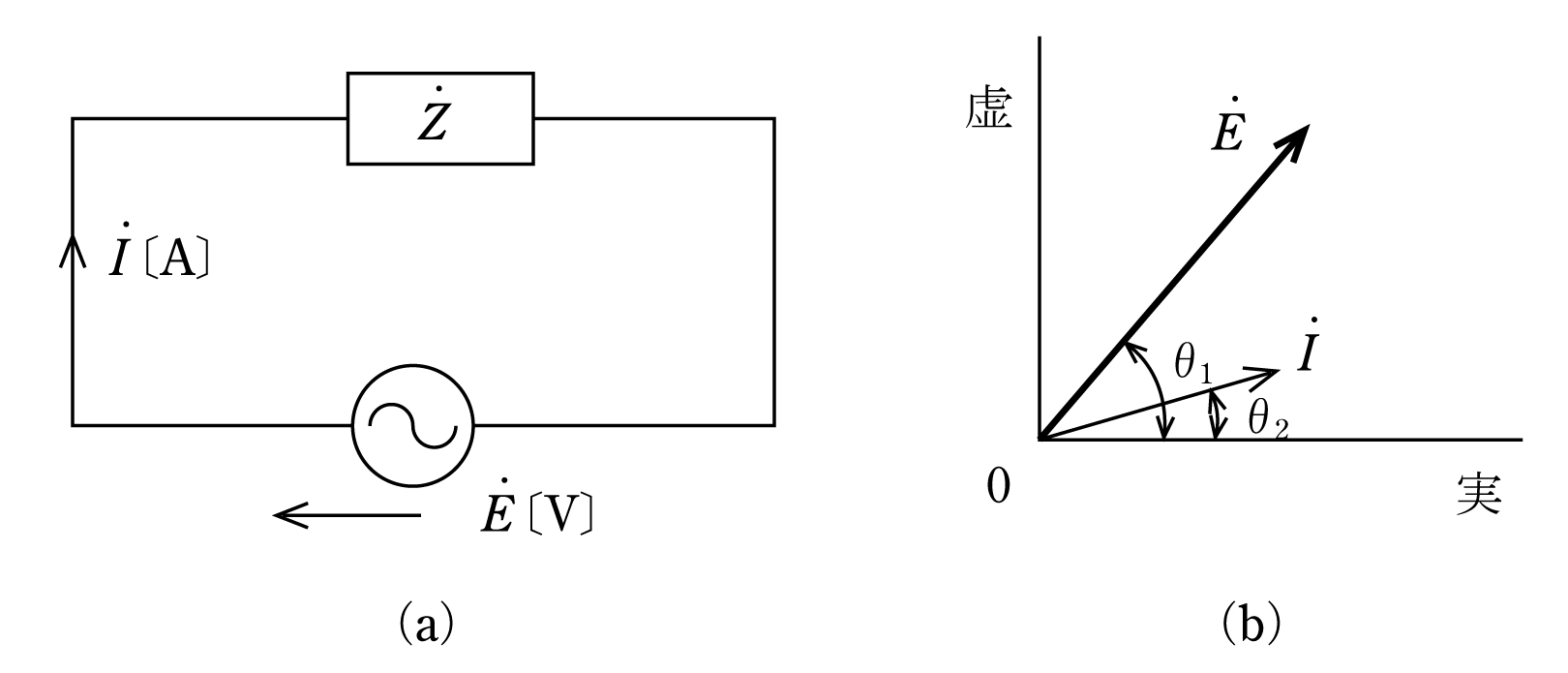
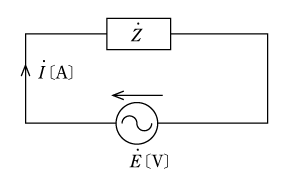
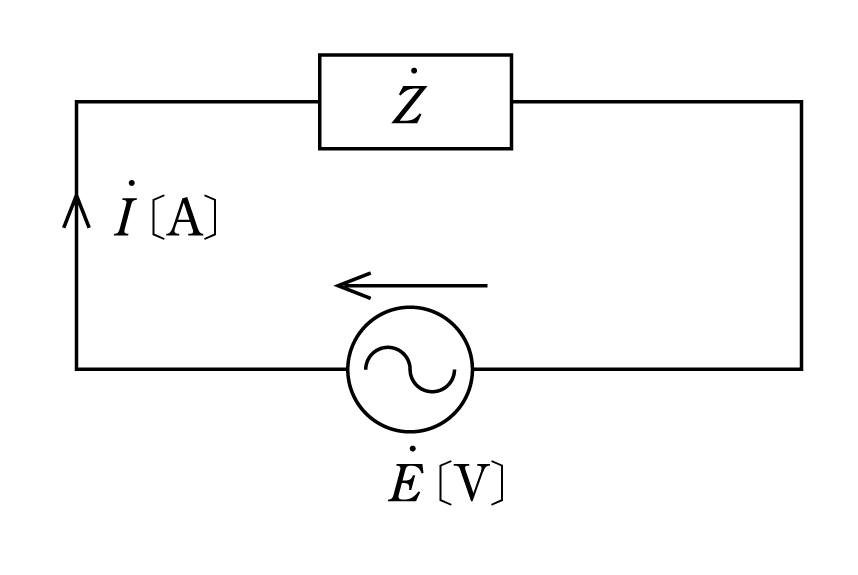
〔問題1〕 第2図(a)の交流回路でインピーダンス
![]()
![]() 〔Ω〕に電圧
〔Ω〕に電圧
![]()
![]() 〔V〕を加えたら、電流
〔V〕を加えたら、電流
![]()
![]() 〔A〕 が流れた。この回路の電力
〔A〕 が流れた。この回路の電力
![]()
![]() 〔W〕を求めよ。ただし、
〔W〕を求めよ。ただし、
![]()
![]() と
と
![]()
![]() は第2図(b)のようなベクトルで示されるものとする。
は第2図(b)のようなベクトルで示されるものとする。
問題1について、さっそく
![]()
![]() を計算してみることにする。まずベクトル
を計算してみることにする。まずベクトル
![]()
![]() を複素数で表してみると
を複素数で表してみると
![]()
![]() 、
、
![]()
![]() となる。この2式を使って計算すると結果的にどうなるであろうか。
となる。この2式を使って計算すると結果的にどうなるであろうか。
=
![]()
![]()
=
![]()
![]()
=
![]()
![]()
* この式の展開は三角関数の加法定理の公式による。
さて(1)式でEI cos(θ1+θ2)は実数部分であり、jEIsin(θ1+θ2)は虚数部分である。そこで、この(1)式が電力を表すかどうかということが問題である。
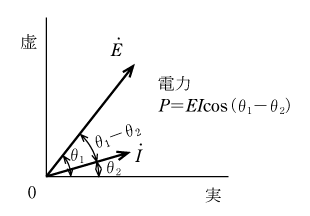
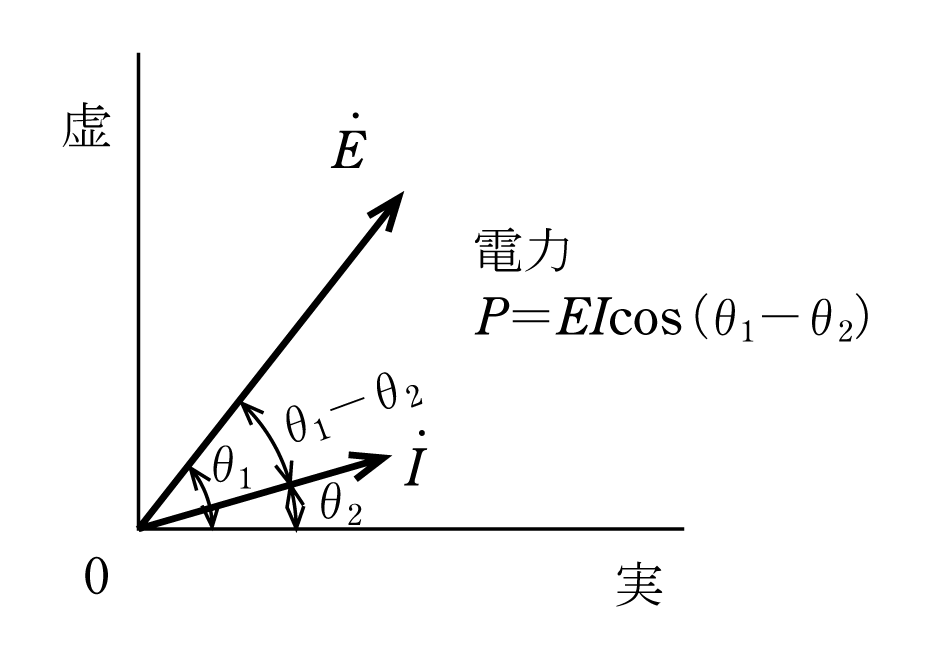
みなさんは、交流の消費電力は電圧の実効値と電流の実効値の積に力率を掛けて求められることを知っているはずである。そこで第3図のこの回路のベクトル図を見てもらいたい。電圧の実効値はE〔V〕、電流の実効値はI〔A〕、そして位相差は(θ1−θ2)であるから、力率はcos(θ1−θ2)のはずである。 したがって、この回路の電力Pの大きさは P=EIcos(θ1−θ2)とならなければいけない。
それでは
![]()
![]() の式のどこがいけなかったのであろうか。(1)式をよく見てもらいたい。実数部分がEI cos(θ1+θ2)となっているが、ここはEI cos(θ1−θ2)でなければならない。
の式のどこがいけなかったのであろうか。(1)式をよく見てもらいたい。実数部分がEI cos(θ1+θ2)となっているが、ここはEI cos(θ1−θ2)でなければならない。
それでは今までの苦労は全部水の泡かというと、そんなことはない。生き返らせる方法があるからご安心。
![]()
![]() に
に
![]()
![]() を掛けただけで複素数計算しても、電力を求める式にならないことははっきりしたが、+θ2が−θ2になりさえすればよいのであるから、なんとか
を掛けただけで複素数計算しても、電力を求める式にならないことははっきりしたが、+θ2が−θ2になりさえすればよいのであるから、なんとか
![]()
![]() を改造して
を改造して
![]()
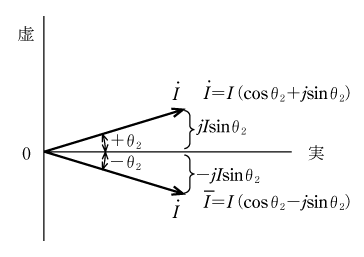
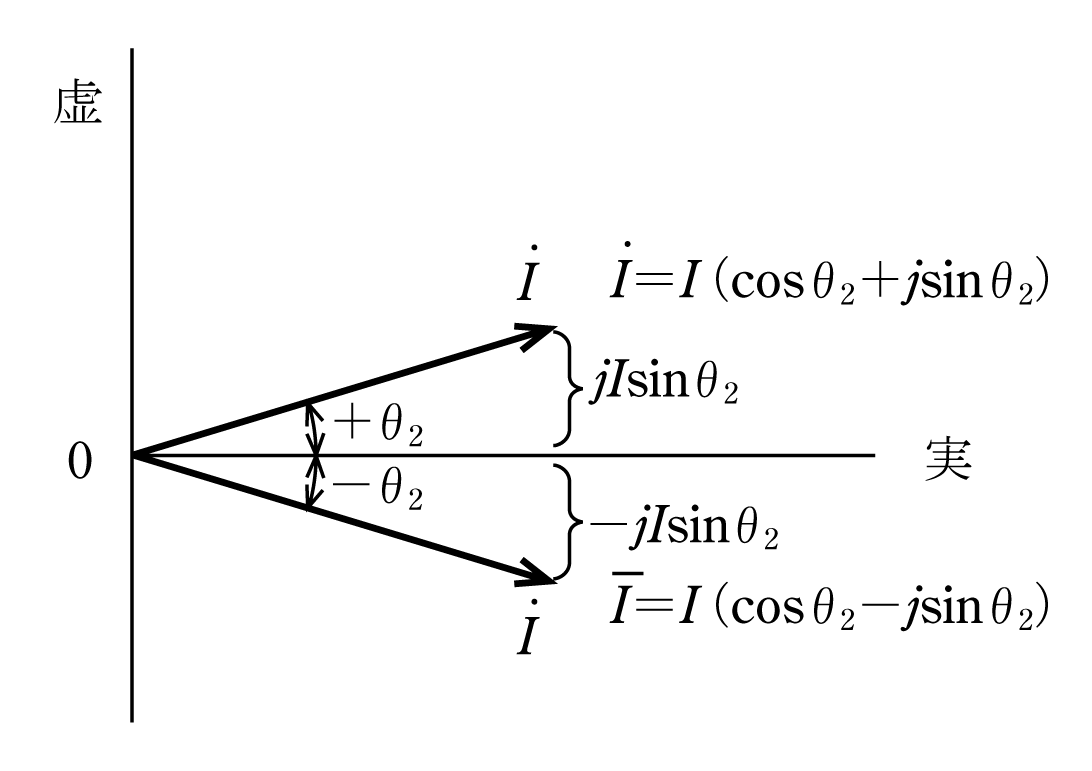
![]() に掛けてやれば電力を求める式が引き出せそうである。θ2というのは位相角であるから、+記号は進みを表し、−記号は遅れを表す。したがって、第4図のように実数軸からθ2進んだ
に掛けてやれば電力を求める式が引き出せそうである。θ2というのは位相角であるから、+記号は進みを表し、−記号は遅れを表す。したがって、第4図のように実数軸からθ2進んだ
![]()
![]() を掛ける代わりに、θ2遅れた
を掛ける代わりに、θ2遅れた
![]()
![]() をわざと
をわざと
![]()
![]() に掛けてやることにする。
に掛けてやることにする。
![]()
![]() に対して、
に対して、
![]()
![]() を共役複素数と呼び、
を共役複素数と呼び、
![]()
![]()
![]()
![]() となる。こんどは
となる。こんどは
![]()
![]() を作ってもう一度計算をし直してみよう。
を作ってもう一度計算をし直してみよう。
見事に実数部に消費電力P=EIcos(θ1−θ2)が出た。問題1はこれが答となる。
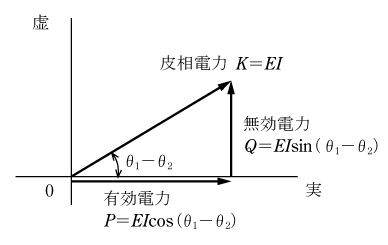
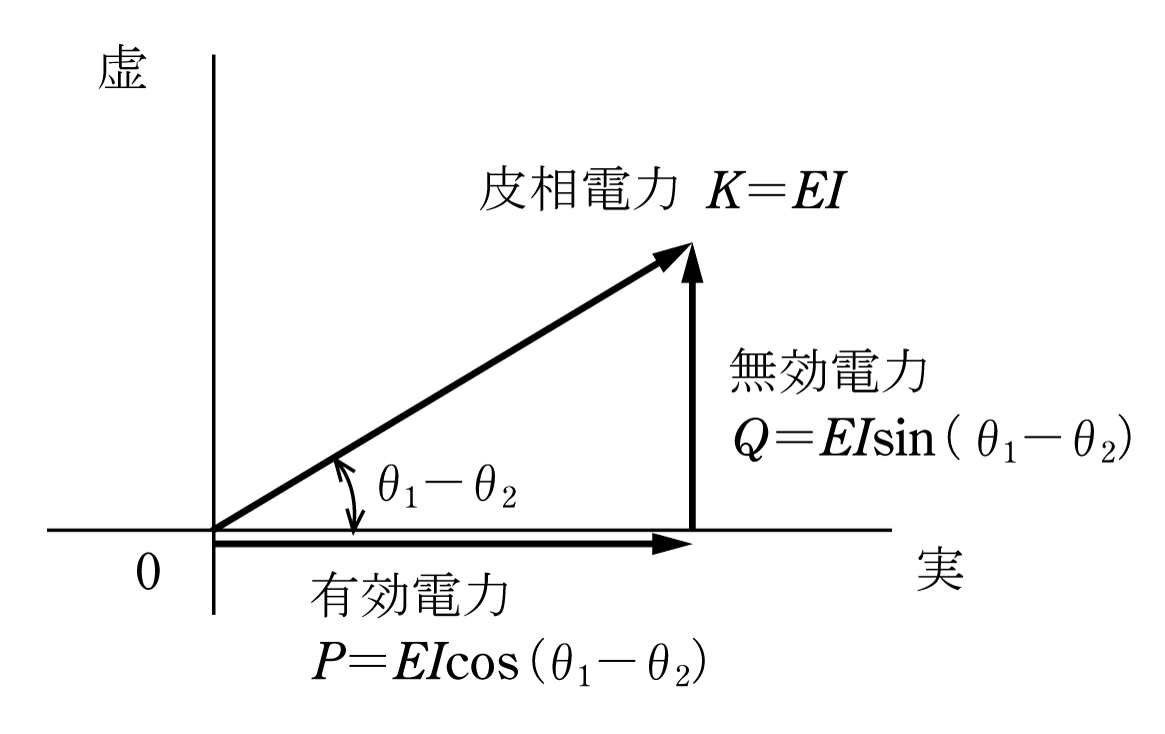
(2)式をベクトル図で示すと、第5図のようになる。
ベクトル図から判断できるように、実数軸上のP=EIcos(θ1−θ2)は有効電力(消費電力)となり、虚数軸上のQ=EIsin(θ1−θ2)は無効電力、ベクトル
![]()
![]() の絶対値は皮相電力を表している。
の絶対値は皮相電力を表している。
![]()
![]() は皮相電力の複素数表示であることが分かる。皮相電力をKとして、要点をまとめておくと次のようになる。
は皮相電力の複素数表示であることが分かる。皮相電力をKとして、要点をまとめておくと次のようになる。
電力の計算では、必ず
![]()
![]() を使うこと。 *
を使うこと。 *
![]()
![]() はダメ
はダメ
K:皮相電力 有効電力:EIcos(θ1−θ2) 無効電力:EIsin(θ1−θ2)
〔問題2〕 第6図の交流回路に
![]()
![]() の電圧を加えたところ、
の電圧を加えたところ、
![]()
![]() の電流が流れた。このとき有効電力、皮相電力、無効電力を計算せよ。
の電流が流れた。このとき有効電力、皮相電力、無効電力を計算せよ。
(解説) ウッカリ
![]()
![]() を計算してしまわないように注意すること。
を計算してしまわないように注意すること。
〔正解〕
![]()
![]()
有効電力 P=1,000 W
無効電力 Q= 500 var
皮相電力
![]()
![]() VA
VA
力率
![]()
![]() %
%
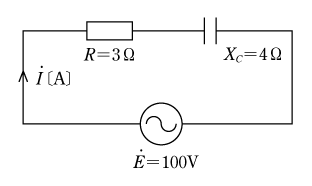
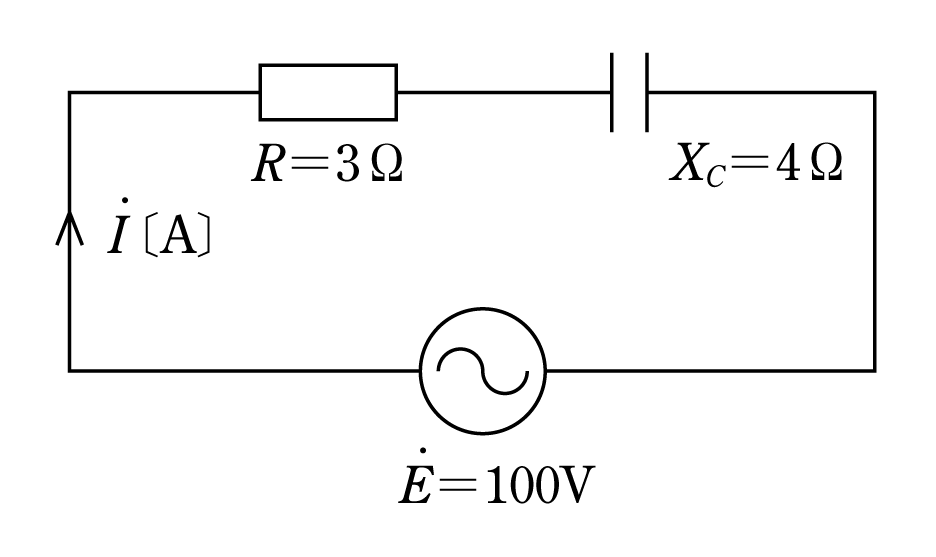
〔問題3〕 第7図の交流回路での消費電力、無効電力、皮相電力、力率を複素数を用いて計算せよ。
〔正解〕
![]()
![]() =100 V
=100 V
![]()
![]()
したがって、
![]()
![]() を計算する。
を計算する。
消費電力 P=1,200 W
無効電力 Q=1,600 var
皮相電力 K=
![]()
![]()
力率
![]()
![]()