〜終わり〜
■ぜひアンケートにご協力下さい■


電磁誘導現象は電気のあるところであればどこにでも現れる現象である。このシリーズは電磁誘導現象とその扱い方について解説する。今回は、インダクタンスを含む交流回路の取り扱いについて解説する。
自己インダクタンスLに印加されている交流電圧と流れる電流は、『インダクタンス物語(2)』で述べたように、第1図の関係にある。
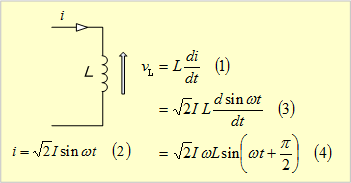
第1図 自己インダクタンスにおける電圧と電流の関係
この結果、印加電圧を次式のvLとすれば、(4)式の関係から、
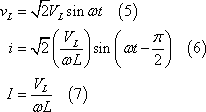
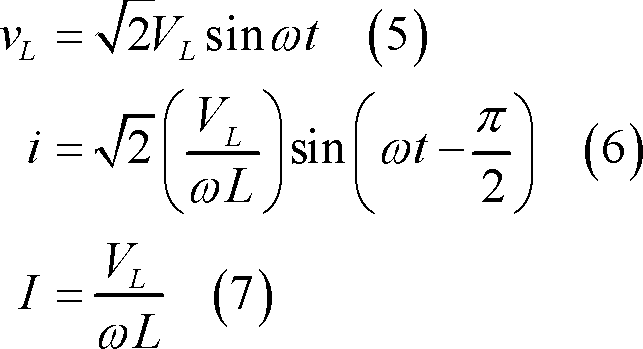
となり、
自己インダクタンスLに交流電圧Vが加わると、V/ωLの電流が電圧より90°遅れて流れる。
【例題1】 10mHの自己インダクタンスに100V、50Hzの交流電圧が印加されているとき、流れる電流はいくらか。
解答 (7)式により求める電流の大きさは、
位相は、印加電圧より90°遅れる。
第2図(a)のように、自己インダクタンスL1、L2を直列接続した場合は、同図(b)の関係から、L1+L2の自己インダクタンス1個と見なして扱ってよいことになる。
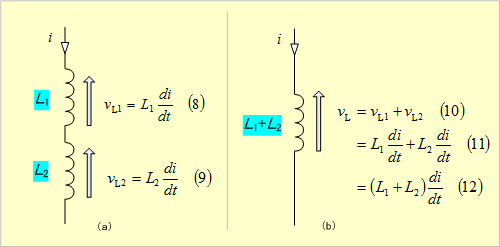
第2図 直列接続
第3図(a)のように、自己インダクタンスL1、L2を並列接続した場合は、同図(b)のような1個の自己インダクタンスとして扱ってよいことになる。
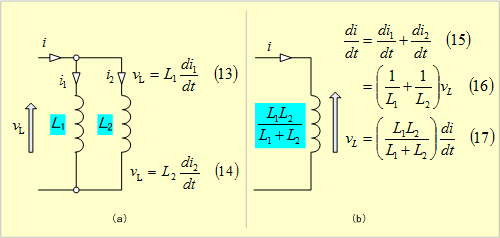
第3図 並列接続
第4図(a)のように、自己インダクタンスL1、L2があり、両者の間には相互誘導作用がある場合は、相互インダクタンスをMとし、自己、相互両作用による起電力の方向が各コイルとも同図(b)のように同方向であるとすれば、電圧と電流の関係は、
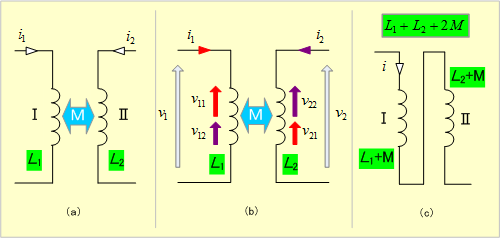
第4図
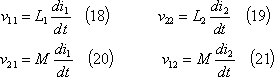
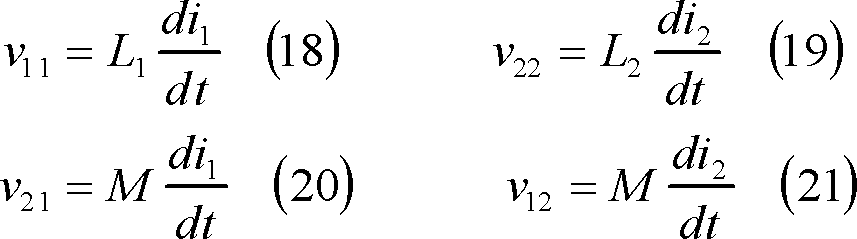
であり、各コイルについて、
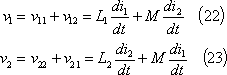
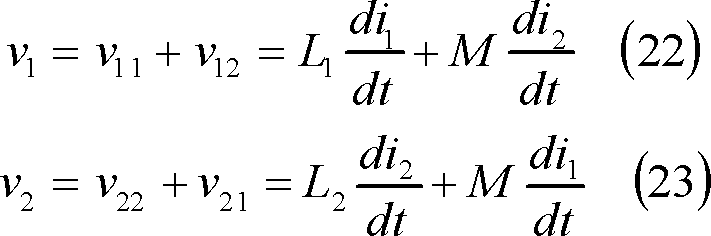
の関係にある。
したがって、同図(c)のように接続すれば、
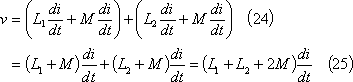
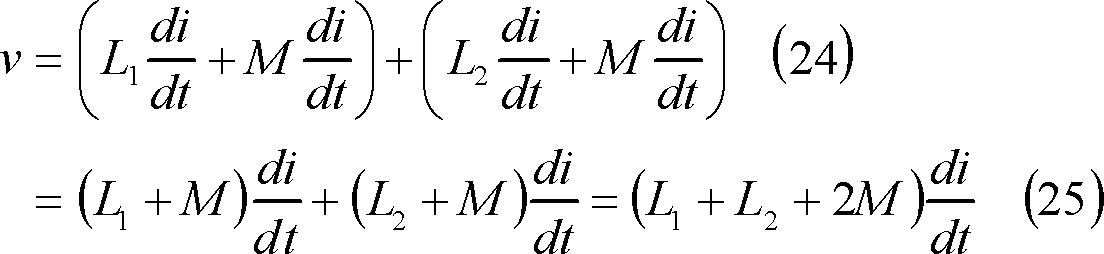
となり、個々の自己インダクタンスがMだけ増したようになり、回路全体としては、
![]()
![]() の自己インダクタンスとして扱ってよいことになる。
の自己インダクタンスとして扱ってよいことになる。
第5図(a)のように、二つのコイルがあり、両コイル間に相互誘導作用があるとき、自コイルがつくる磁束の一部が他コイルと鎖交する磁束を相互誘導作用の原因となる磁束という意味から相互磁束と呼ぶことにする。この相互磁束が同図(a)のように互いに加わるような関係にある場合を、和動的といい、互いに打ち消し合う場合を差動的という。
これらの電磁気的な結合関係は図記号だけでは表示できないので、電気回路上では図記号端に●印(ドット)を傍記して明示する。そして、両コイルの●側端子から電流が流入(流出)する場合には相互磁束が加わり合うと約束する。この結果、和動的な場合は同図(b)、差動的な場合は同図(c)のようにそれぞれ表示する。
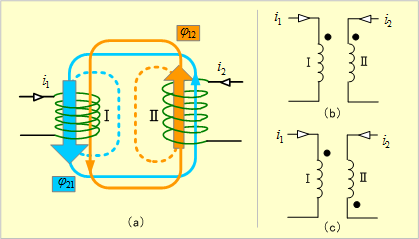
第5図 和動と差動
【例題2】 第6図の各回路を自己インダクタンス回路で表せ。
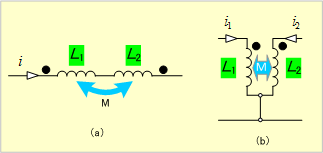
第6図
解答 第6図(a)の回路は差動接続なので、回路両端の電圧vは、
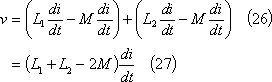
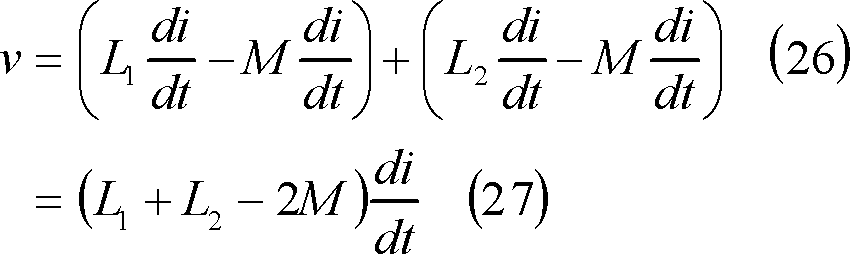
となる。したがって、第7図(a)が答となる。
第6図(b)の回路では、和動的なので次の2式が成立する。
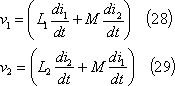
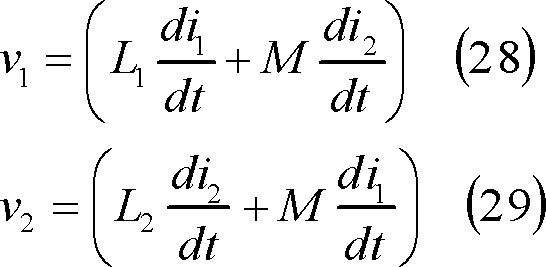
ここで、両式右辺第2項は、
の関係にあるので、第7図(b)が答となる。
第7図
第8図(a)のように、抵抗Rと自己インダクタンスLとが直列接続されている回路に正弦波交流電圧vが加えられている状態では、回路にはどんな電流が流れるか、調べてみよう。
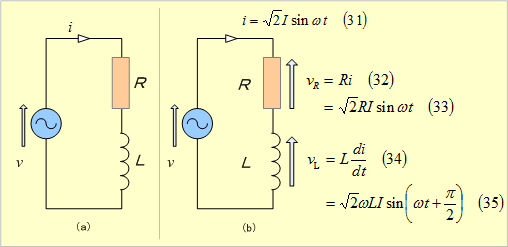
第8図 交流RL直列回路
正弦波交流電源に接続されている回路は、『インダクタンス物語(2)』で説明したように、定常状態では回路を流れる電流も正弦波交流となる。このため、第8図(b)において電流iを(31)式と仮定すれば、回路素子端の電圧は図中の各式となるので、回路への印加電圧とは次式の関係にあり、その波形は第9図のようになる。
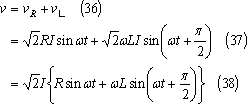
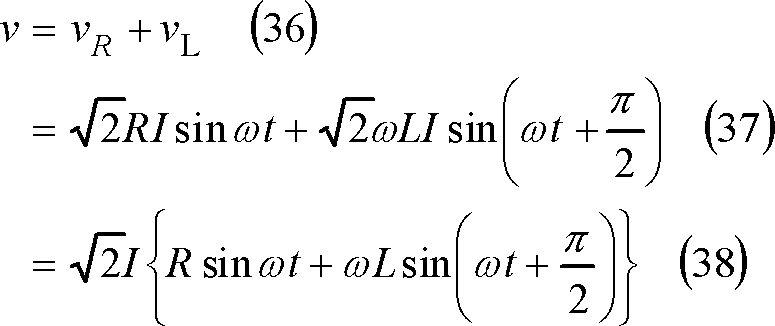
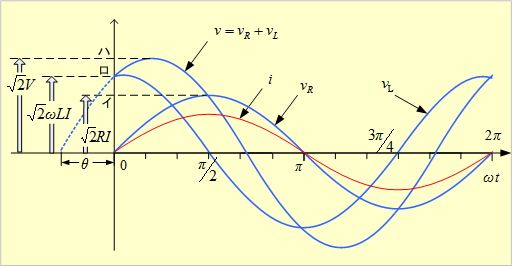
第9図 電圧と電流の波形
(38)式右辺の{ }内のような二つの正弦波は、次の三角関数公式によって一つの正弦波に合成できる。
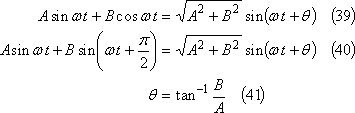
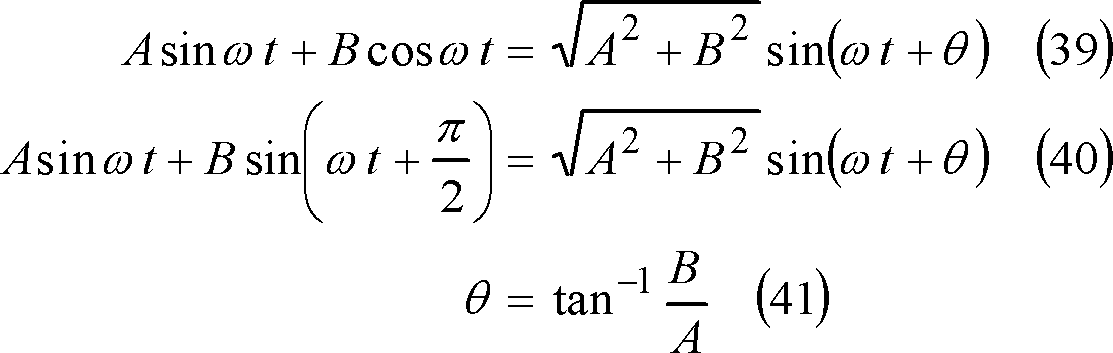
したがって、(40)式を(38)式に応用すれば、電圧vは、
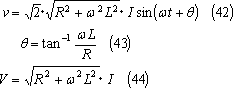
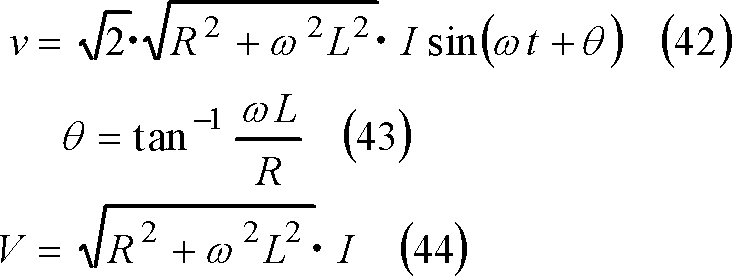
この結果、下記のように、回路に電圧vを加えると電流iが流れ、電流iの大きさはI、iはvよりθ遅れて流れることがわかる。
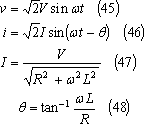
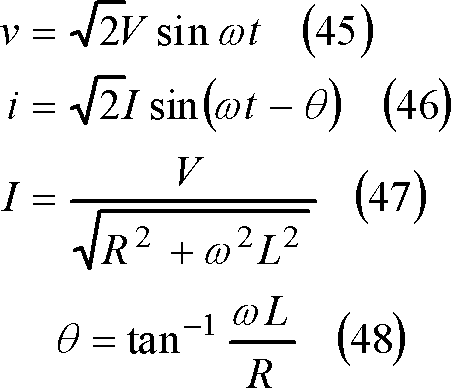
これらの関係は次のように図式的に求めることができる。
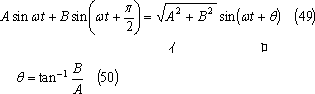
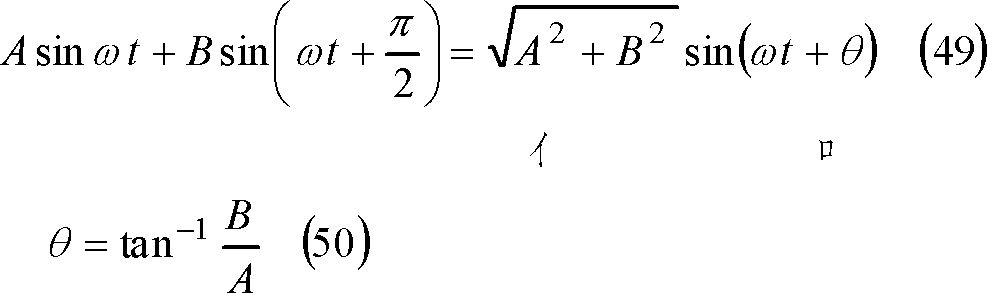
について、第10図(a)を描けば、同図から、大きさ(実効値)は、
![]()
![]() と
と
![]()
![]() の和
の和
![]()
![]() の斜辺Cで、相差角θは
の斜辺Cで、相差角θは
![]()
![]() の偏角で、それぞれ求めることができる。
の偏角で、それぞれ求めることができる。
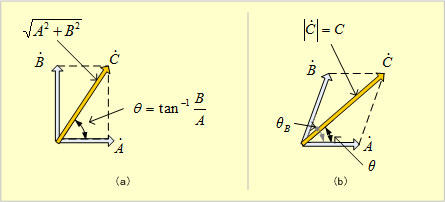
第10図 大きさ(実効値)と相差角の関係
一般的には、(51)式左辺のように両正弦波間の相差角θBである場合は、同図(b)のベクトル図から、大きさと相差角が簡単に求まり、右辺のように、合成波を求めることができる。
ここで、
![]()
![]() とすれば、
とすれば、
![]()
![]() の大きさは次の余弦定理により、
の大きさは次の余弦定理により、
となるので、
![]()
![]() は、
は、
として、相差角θは.第10図(b)の関係から、
![]()
![]() の縦軸成分と横軸成分の比から、
の縦軸成分と横軸成分の比から、
として、それぞれ求めることができる。
それでは、これまでの関係を第11図で各再生ボタンを押して確認しておこう。
① RL直列回路に交流電流を流したとき、電流と、RとLの端子電圧が波形で観察できる。
観察の結果、回路に電流i が流れていると、抵抗端にはiと同相に電圧vRが、インダクタンス端にはiより90°位相の進んだ電圧vLが、それぞれ現れ、回路の両端の電圧は両者の和である電圧vが現れる、という関係が確認できる。
② 回路各部の電圧波形を観察し、電圧相互の関係に注目しよう。
ここでは、各瞬時について、v=vR+vLが成立していることを確認する。
③ vR、vLをベクトルに置き換えると、合成電圧vの大きさと相差角θをベクトル図から簡単に知ることができる。
④ 印加電圧vと電流iとの関係を示す量をベクトル図が握っていることを理解しよう。
⑤ 初位相が零の電圧が印加されているときの電流波形をしっかりと確認しよう。
第11図
第12図のように、RとLが並列接続された回路の場合、端子電圧と電流との関係は、次のようになる。
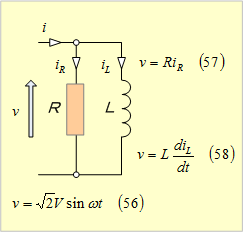
第12図 RL並列回路
電流iは、
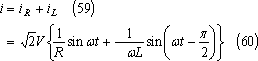
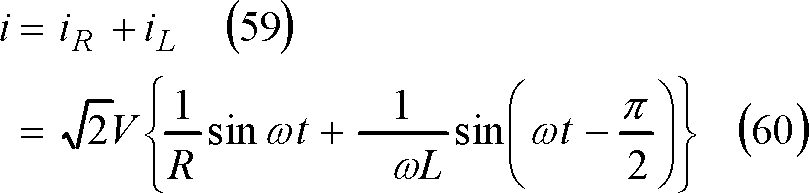
電流の大きさIは、
電圧vとの相差角θは、
(1)自己インダクタンスの電圧と電流の関係 ・・・・・ 第1図、(5)式、(6)式、(7)式
(2)自己インダクタンスの接続 ・・・・・ 第2図、第3図
(3)相互インダクタンス回路 ・・・・・ 第4図、(25)式
(4)コイル間の電磁気的結合関係 ・・・・・ 和動と差動、第5図
(5)交流RL直列回路の性質 <端子電圧と電流との関係(大きさと位相)>
・・・・・ 第8図、(45)式〜(48)式、第11図⑤
(6)交流RL並列回路の性質 <端子電圧と電流との関係(大きさと位相)>
・・・・・ 第12図、(60)式〜(62)式
