〜終わり〜
■ぜひアンケートにご協力下さい■


電磁誘導現象は電気のあるところであればどこにでも現れる現象である。このシリーズは電磁誘導現象とその扱い方について解説する。今回は、インダクタンスを含む直流回路の取り扱いについて解説する。
第1図のRL直列回路で、t=0の時スイッチSを閉じて回路に直流電圧Eを印加すると、回路にどのような電流が流れるだろうか。
第1図 直流RL直列回路(起電力印加時)
① 第1図の再生ボタンを押して、t=0でSを閉じたとき、回路に流れる電流を観察してみよう。
それではどうしてこのような電流が流れるのか考えてみよう。この場合の回路の電圧方程式は次式となる。
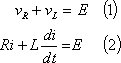
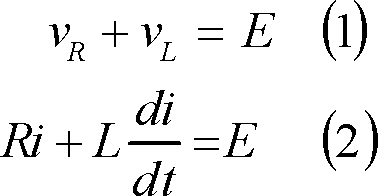
ここで、求める電流iを、I1、I2、αを定数として、次式のようにおく。
この場合の回路条件は、
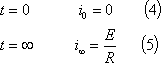
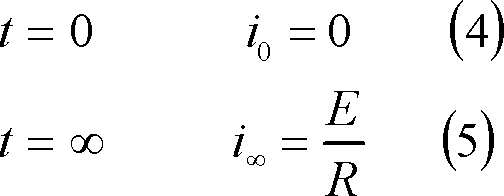
であり、(4)の条件を(3)式に代入すれば、
(5)式の条件と(7)式の関係を(3)式に代入すれば、
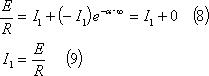
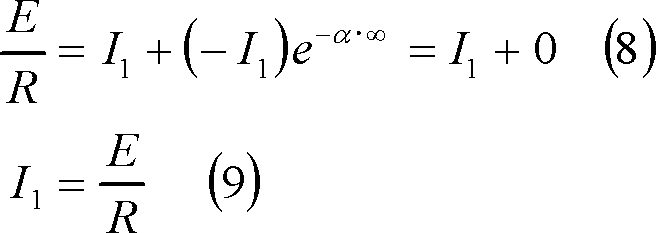
したがって、電流は、
となる。ここで、上式を(2)式に代入すれば、
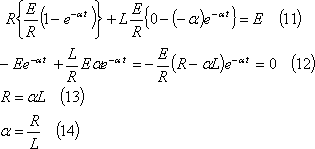
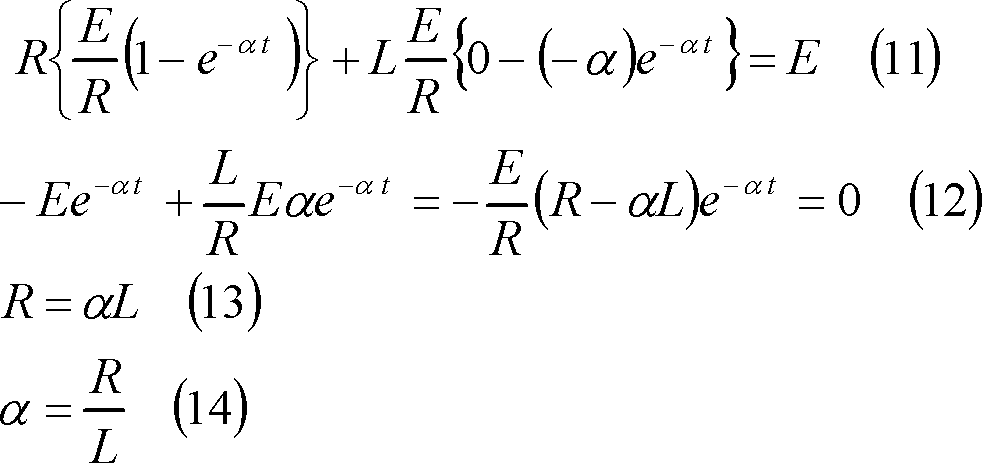
となり、αが求まるので、これを(10)式に代入して、
となり、電流の式が求められる。
この結果、電流の勾配は、上式から、
で求められるので、t=0における電流勾配は、
となる。
したがって、第2図に示すように、電流はS投入前の値(初期値)である零から(17)式に示す勾配で流れはじめ,以後(16)式に従い、勾配は次第に緩やかになり、ついには零となるため、図のような電流変化になるわけである。
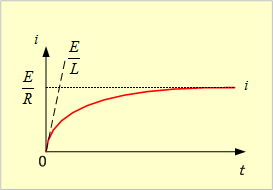
第2図 電流の時間的変化
② 再生ボタンを押して、電流の変化に対するR端とL端の電圧がどのように変化するか観察してみよう。
R端電圧とL端電圧は、
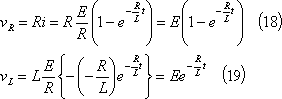
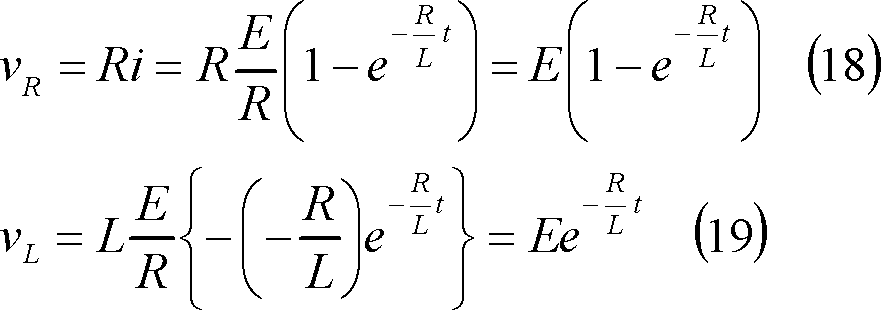
となる。
第3図の回路において、図の状態にあるとき、t=0でSを開くと同時にS´を閉じると、回路にはどんな電流が流れるか、調べてみよう。
第3図 直流RL直列回路(起電力開放時<その1>)
① 再生ボタンを押して、このとき流れる電流を観察してみよう。
Sを開きS´を閉じたときの回路の電圧方程式は、次式となる。
ここで、求める電流iをI1、I2、αを定数として、次式のようにおく。
この場合の回路条件は、
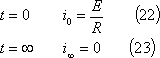
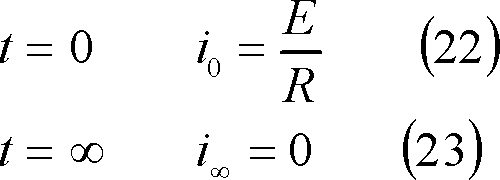
で、(22)式の条件から、
(23)式の条件から、
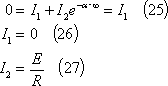
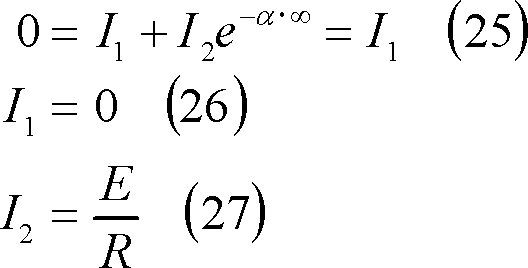
となるので、
このため、t=0における回路の電圧方程式は、(29)式となるので、αは(30)式となる。
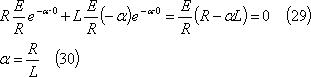
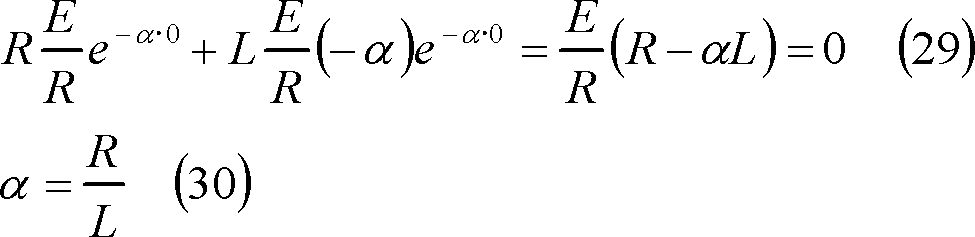
したがって、電流は、
となる。
このため、電流の勾配は、
t=0における電流勾配は、
電流はLの性質によって、S開放直前に回路を流れていた電流(初期値)「E/R」を起点として、(33)式で決まる勾配で流れはじめ、以後(32)式の勾配で変化するので、電流は図のように緩やかな変化になり、ついには零という一定値に落ち着くことになる。
② 再生ボタンを押して、Sを開いたとき流れる電流とR端とL端の電圧を観察してみよう。
S開放後のR端電圧は、
Lを含む閉路では、
![]()
![]() が常に成立しているので、L端電圧は、
が常に成立しているので、L端電圧は、
となる。このため、vRとvLは図のように横軸に対して対称な電圧として変化していることが分かる。
第4図の回路は、第3図の回路でスイッチS´を抵抗R´に置き換えた回路である。この回路において、t=0でスイッチSを開くと、どんな現象が起こるだろうか、観察してみよう。
第4図 直流RL直列回路(起電力開放時<その2>)
① 再生ボタンを押して、Lに流れる電流iを観察してみよう。
この場合の電流の式は次式となる。
② 再生ボタンを押して、第3図の回路で流れた電流(点線)と比較してみよう。
第4図の場合の電流勾配は、
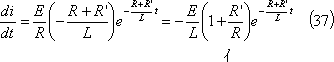
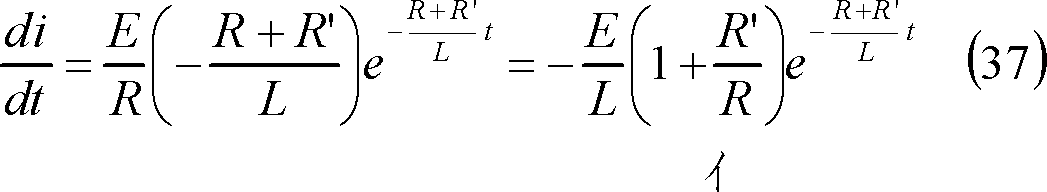
であり、t=0における電流勾配は、
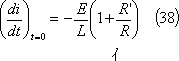
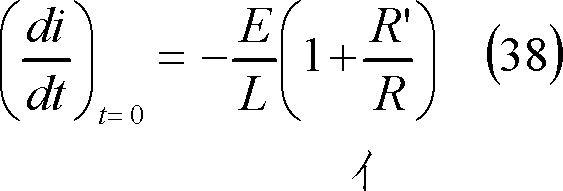
である。したがって、電流は初期値がE/Rで、(38)式のように第3図の場合のイ倍の勾配で流れはじめ、以後、(37)式に示すように時間の経過と共に第3図のイ倍の急な勾配で流れ、ついには零となる。
③ 続いて、再生ボタンを押して、電流に対する各部の電圧の関係を観察してみよう。
各部の電圧は、第3図の場合のRをR+R´に置き換えたものに等しく、
となる。S開放後の閉路では、電圧方程式
が常に成立しており、
の関係にある。
④ 再生ボタンを押して第3図の場合の電流と回路各部の電圧(点線)と比較してみよう。
それでは第3図とどうしてこのような差が出てくるのか考えてみよう。
Sが開いた時、Lを含む閉路では、Lの性質によりS開放直前の電流であるE/R(=i0)から電流の変化がはじまる。このため、S開放時、抵抗による電圧降下は第3図の回路では、
であるが、第4図の場合は(45)式であり、
![]()
![]() とおけば、(46)式となる。
とおけば、(46)式となる。
電流は、
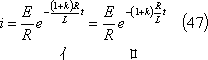
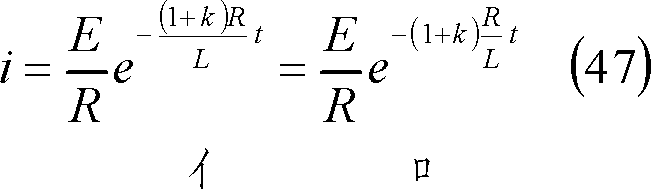
電流勾配式は、
Lの端子電圧vLは、
となる。つまり、電流勾配は、第3図のように抵抗がRだけの場合に比べ、(1+k)倍と急峻になり、その結果としてvLも(1+k)倍と大きくなることがわかる。
t=0において、電流勾配は、
抵抗による電圧降下は、
であり、vLは(43)式から、
となる。
つまり、第3図と第4図の回路の違いは、S開放後にできるLを含む閉路における抵抗分が「R」か「R+R´」かの違いであり、具体的には第4図の方が第3図よりもR´だけ増すことになる。
t=0のときは両回路ともLの性質で初期電流はE/Rで同一である。このため、この瞬間の抵抗による電圧降下は第4図の回路は第3図に比べ、(1+k)倍となる。この結果、L端電圧は(52)式に示すようにこれと同一の値を要求され、Lではこの電圧をつくるために電流勾配をより急峻にして対応するわけである。
以上のことから、kが非常に大きい場合、具体的にはR´がつながれていないような場合、実際は、このようなケースが多いわけであるが、このような場合はS開放時に急激な電流変化が起こり、
![]()
![]() は非常に大きな電圧となる。このため、S開放時、Sの極間にはこの電圧と等しい電圧が現れ、空気の絶縁が破れ火花が発生することになるわけである。
は非常に大きな電圧となる。このため、S開放時、Sの極間にはこの電圧と等しい電圧が現れ、空気の絶縁が破れ火花が発生することになるわけである。
コイルのようにLを含む回路等でスイッチを切る瞬間に極間部に火花が見られるのは、このような原因によることが多い。
(1)直流RL直列回路の性質(電圧印加時) 《電流と端子電圧の関係》
・・・・・・ 第1図、(15)式、(18)式、(19)式。
(2)直流RL直列回路の性質(印加電圧消失時) 《電流と端子電圧の関係》
・・・・・・ 第4図、(36)式、(39)式、(40)式、(41)式。
(3)電気回路で電流しゃ断時に火花が発生する原因
