の平衡三相電圧
〜終わり〜
■ぜひアンケートにご協力下さい■
電気理論や電力などの計算問題は､電気工学の法則の意味を理解し､幅広く数学の知識を応用して解かなければならないが、試験会場ではあまり時間をかけることはできないため、方針を素早く決定し要領よく計算する必要がある。しかし、その方針次第で落とし穴にはまり、誤答したり時間がかかって解答が求まらないことがある。このシリーズでは、このような落とし穴の例をいくつか取り上げ、計算運用の上手なテクニックを学ぶ。今回は、不平衡三相負荷の計算について解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
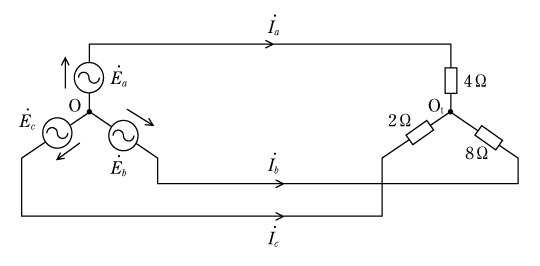
この回路を見て、あっさりと次のような解答を作成した生徒がいたが、これは誤りである。どこに誤りの原因があるのであろうか。
〔答〕 負荷の各相に加わる電圧をベクトルオペレータ
を用いて表すと、
次のようになる。
したがって、
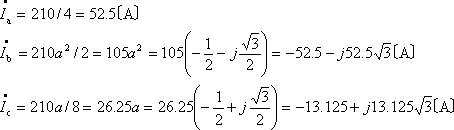
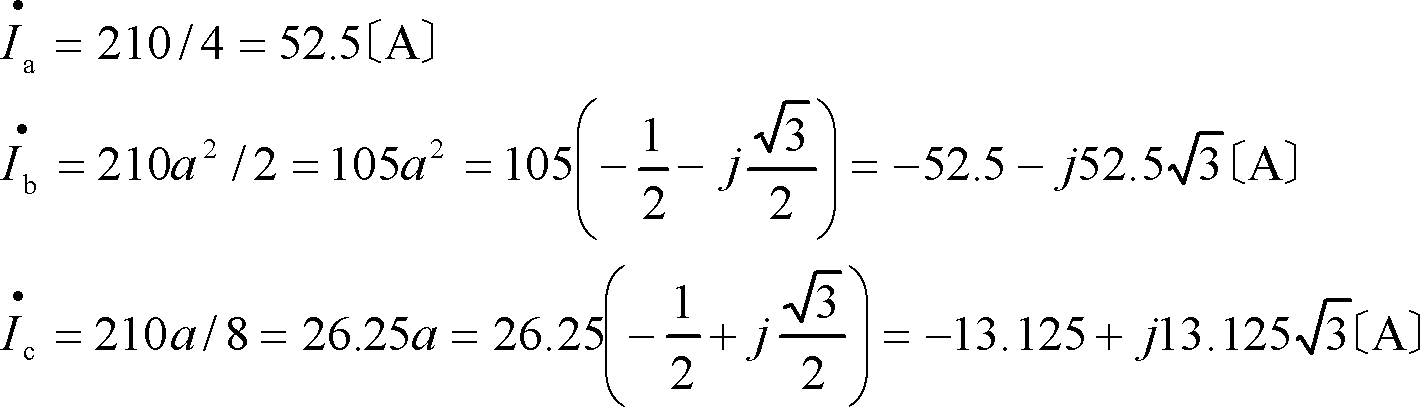
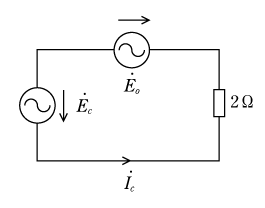
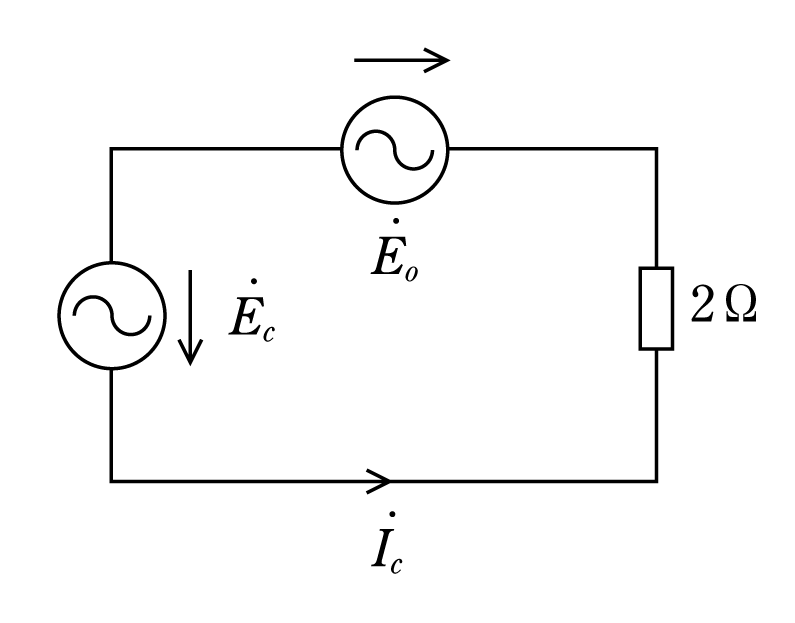
この答案の内容はいかにもあっていそうな感じがするかもしれないが、正解にはほど遠いものである。まず、誤りを確認する方法としてキルヒホッフの第一法則を適用し、負荷側の中性点（Ot）にこれを当てはめてみると、
にならなければならないが、実際に答案の数値を当てはめてみると、
となって、0にはならない。0にならないことはキルヒホッフの法則に反し、この答が正しくないことを示している。
更にこの答案の誤りの原因は、この回路は不平衡回路なのであるから、4、2、8Ωの負荷の両端に生じる電圧は、それぞれ異なっていることに気がついていないことである。
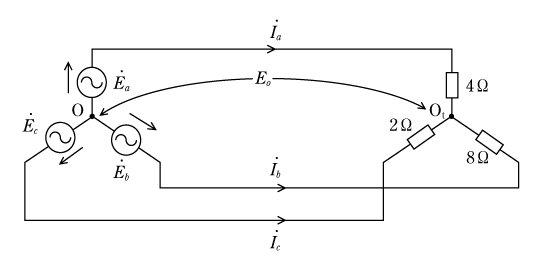
したがって、電源側の中性点Oと、負荷側の中性点Otとの間に生じる電位は、等しくないはずであるから、電源側の中性点Oと負荷側の中性点Otとの間には電位差が生じていることになる。この電位差を計算の過程で考慮しなければならない。
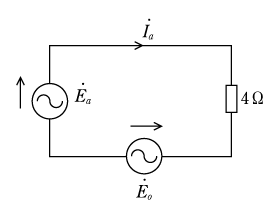
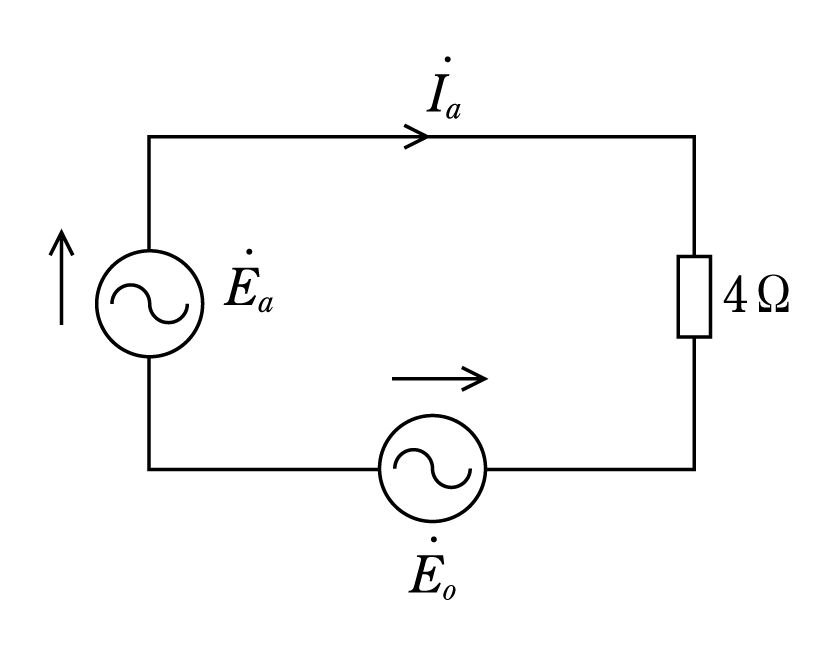
この問題を正しく解くには、この中性点間に生じている電位差をE0と仮定して、このE0を用いて次のようにこの第2図の回路を三つの部分に区分けして考え、キルヒホッフの第二法則を適用し、Ia、Ib、Icを求めることである。
すなわち、第3図は
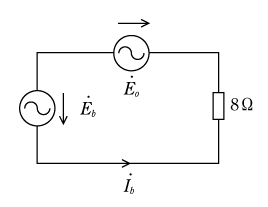
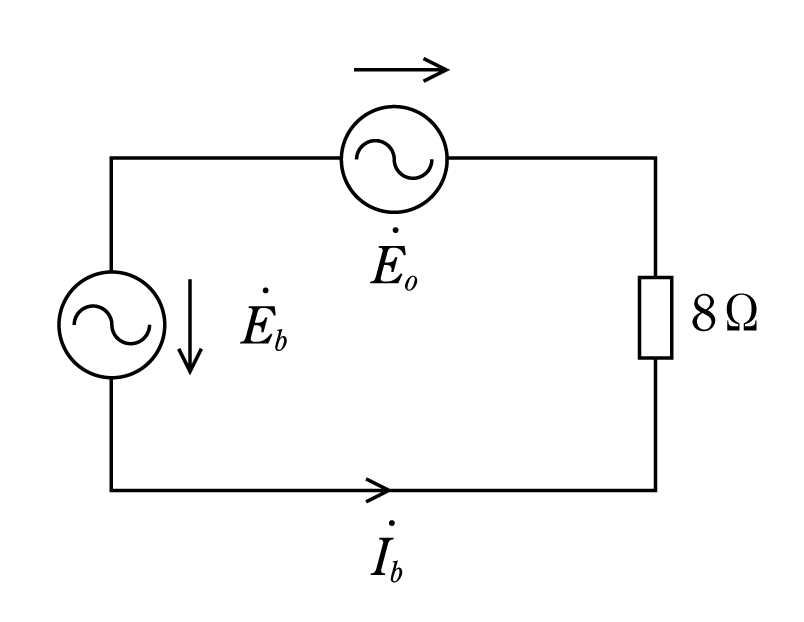
第4図は
第5図は
がそれぞれ成立していることになる。再びキルヒホッフの第一法則を用いて、第3、4、5図から得られた式を
に代入して計算し、0と置いてE0を求める。
この式から、E0を求めると、
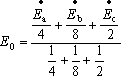
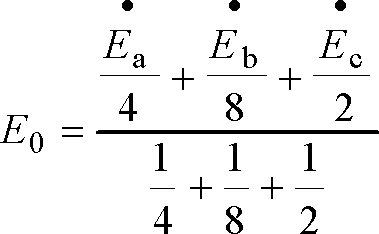
ここで、
は平衡三相電圧であるから、
となり、上式に代入すると、
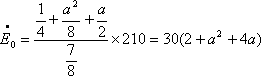
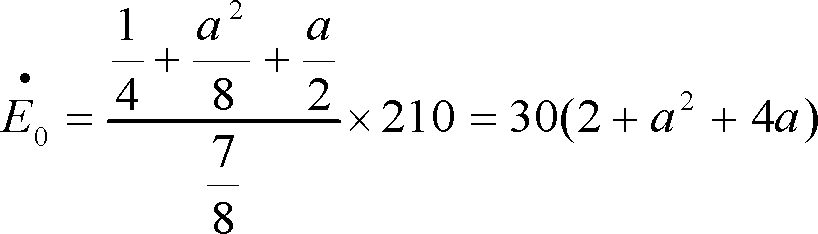
となる。ここで得られた
の値を
に代入すれば、不平衡負荷を流れるそれぞれの値を求めることができる。
〔A〕
〔A〕
〔A〕
〔A〕
〔A〕
〔A〕
ここで、念のため検算をしてみると、
となって、答が正しいことが分かる。
このように不平衡回路の計算は苦労が多いと思われるかもしれないが、複素数を上手に生かした処理ができる方法もあるということを知って、ベクトルオペレータ
の取扱いにも慣れてほしいと思う。
実際には三相不平衡回路は仮にこの例題のように、電源起電力が平衡三相電圧であったとしても、電源内部、電路、負荷の各インピーダンスのうち、少なくとも1種類は不平衡であるから、各電流の状態は異なるものになり、簡単には電流は決定できない。厳密には対称座標法で扱うわけであるが、一般には電源は対称起電力を発生するものであり、内部インピーダンスも平衡しているのが普通であるから、不平衡電流が流れても独立性を失うことなく、変動しないものと扱っても、大きな相違はないものとして処理する。