〜終わり〜
■ぜひアンケートにご協力下さい■


電磁誘導現象は電気のあるところであればどこにでも現れる現象である。このシリーズは電磁誘導現象とその扱い方について解説する。今回は、交流誘導起電力の発生とトルクについて解説する。
運動エネルギーで基本となる関係式を第1図に示す。
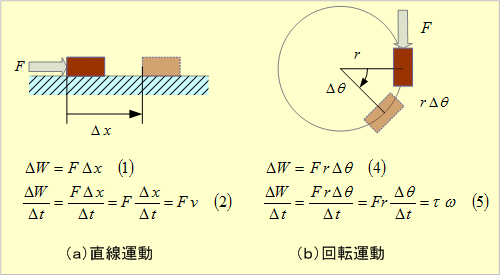
第1図 運動エネルギー(仕事・動力)に関する関係式
直線運動の場合は、力をF[N]、速度をv[m/s]とすれば、パワー(動力)pは、
回転運動の場合は、トルク(回転力)をτ[Nm]、回転角速度をω[rad/s]とすれば、パワーpは、
の関係にある。
第2図(a)のように、磁束密度B[T]の平等磁界中で、同図(b)のようなa[m]、b[m]を辺とした巻数Nの長方形コイルを回転させる(①)と、どんな現象が起こるだろうか。
(1) 準備 コイルの面を上向きとしたコイル断面図である同図(c)に置いて、コイルの軸(矢印の方向)に対して右ねじの関係にある方向を正の方向と約束すれば、図のように、左側b導体b1では●(ドット)が、右側導体b2では×(クロス)が、それぞれ正の方向ということになる(②)。
第2図 磁界中でコイルを回転させる
(2) このコイルを第3図のように、回転角速度ω[rad/s]で反時計方向に回転させて(①)、コイルの軸が上向きの位置から時間を起算すると、時刻t[s]におけるコイルの位置は②となり、このときの鎖交磁束
![]()
![]() は、
は、
となるので、コイルでは、次式の起電力eがコイル端C1C2に誘導される(③)。
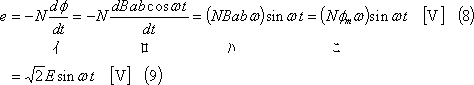
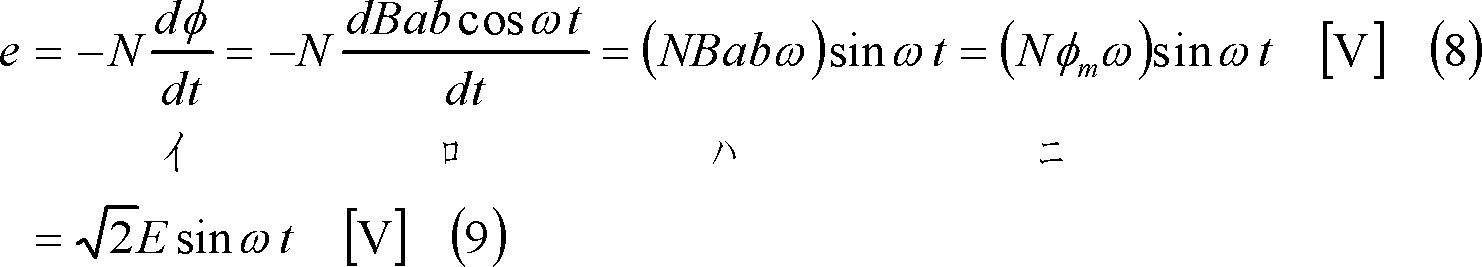
ただし、
![]()
![]() 、
、
![]()
![]()
第3図 磁界中で回転するコイル ―その1―
(3) ここで、コイル端C1C2にスリップリングを介して外部に抵抗を接続すると、この時の抵抗がコイルの内部抵抗を含めてR[Ω]であれば、コイルには次式の電流が流れる(④)。
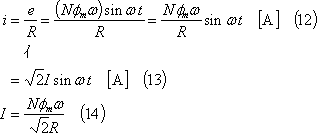
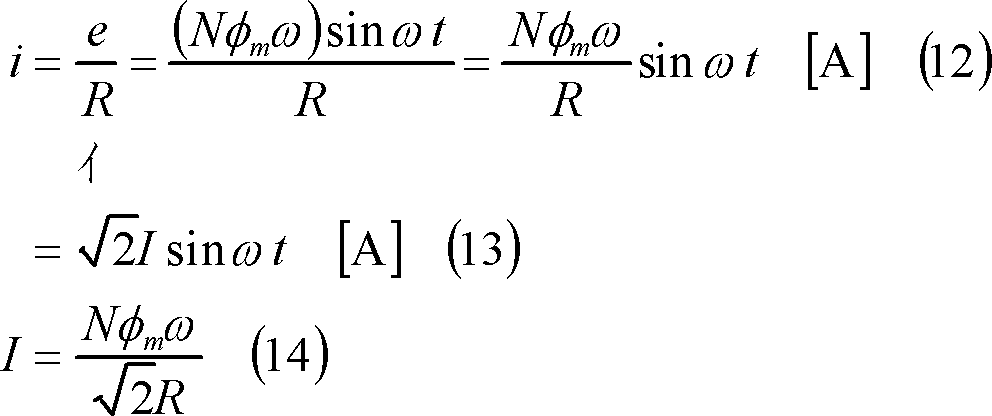
(4) この結果、コイルには、この電流と磁界によって電磁力fa、fbが作用する(⑤)。
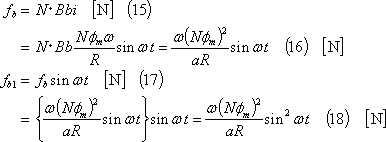
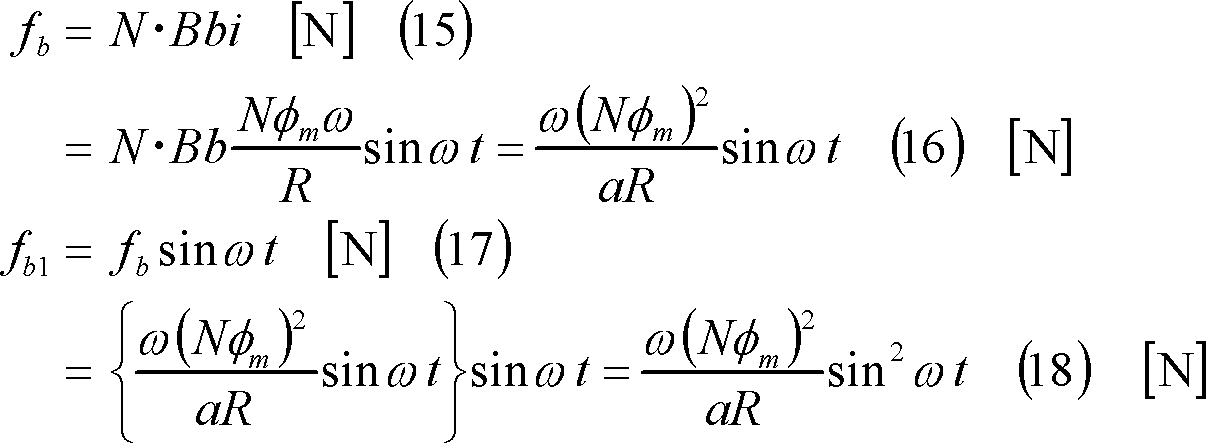
(5) この電磁力の内、b導体に作用する電磁力fb1はコイルを時計方向に回転させるように働く。このため、コイルには次式のトルク(回転力)が作用する。
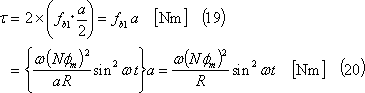
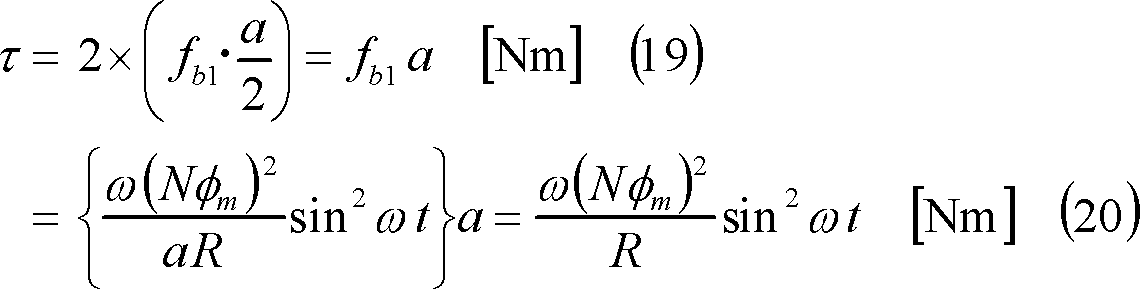
(6) 別解 (3)において、コイルには、起電力eと電流iによって電力pが発生する(⑥)。
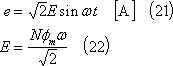
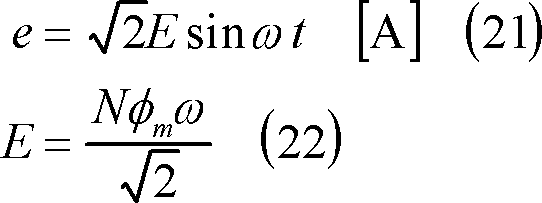
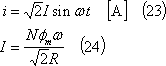
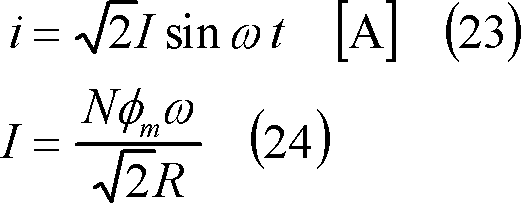
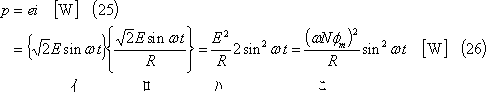
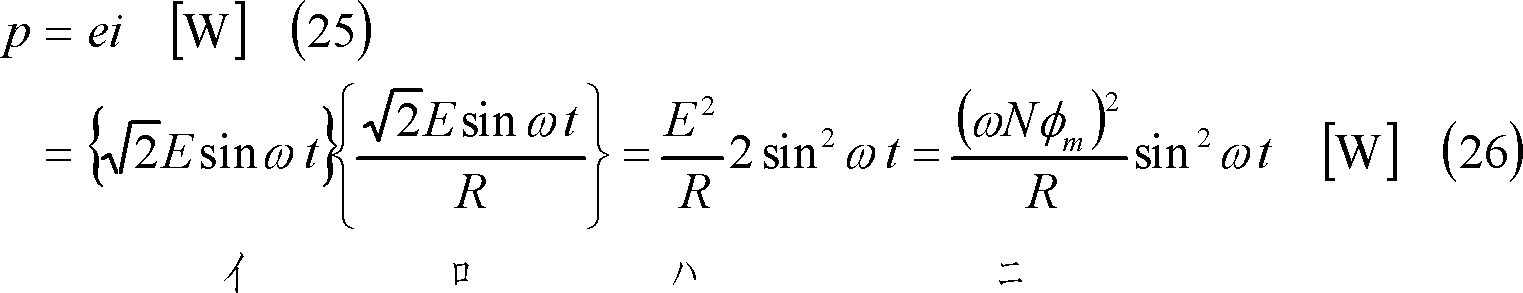
(7) この電力は回転動力が変換されたものであるから、そのトルクτは(6)式の関係から次式となる。
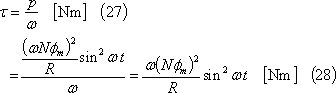
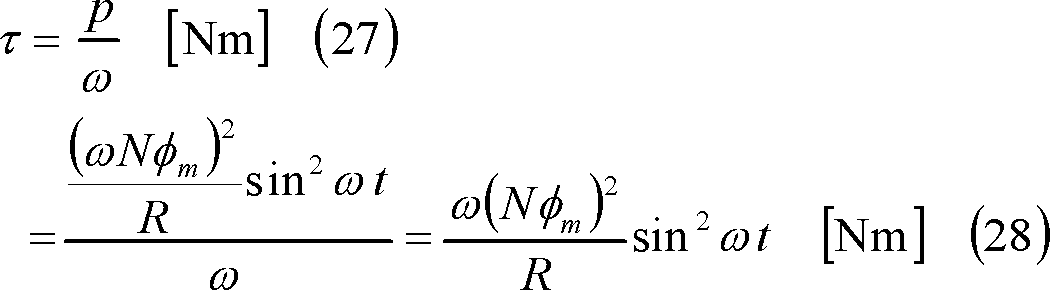
(8) この場合、コイルに発生したトルクは⑦に示すように時間とともに変化するが、その平均値である平均トルクTは、次式で示される(⑧)。
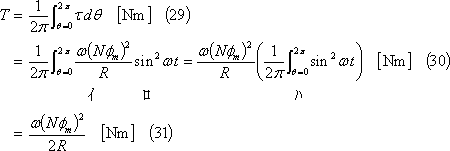
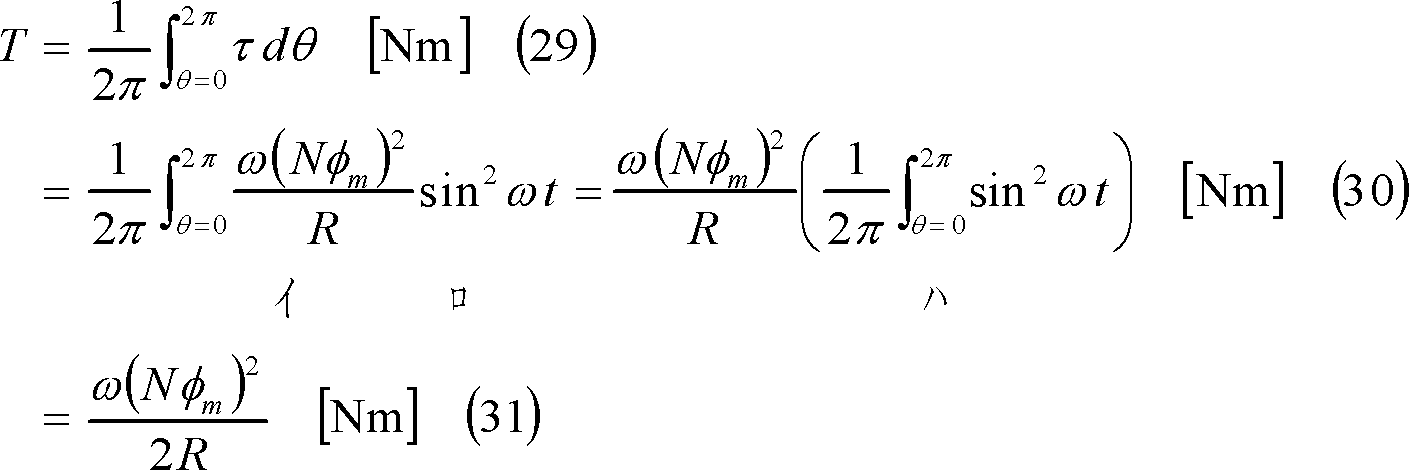
(9) Tの別解 (27)式は、平均値についても成立するので、次のようにしてTを求めることができる。
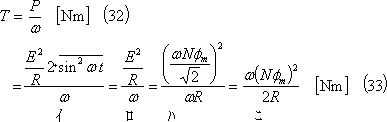
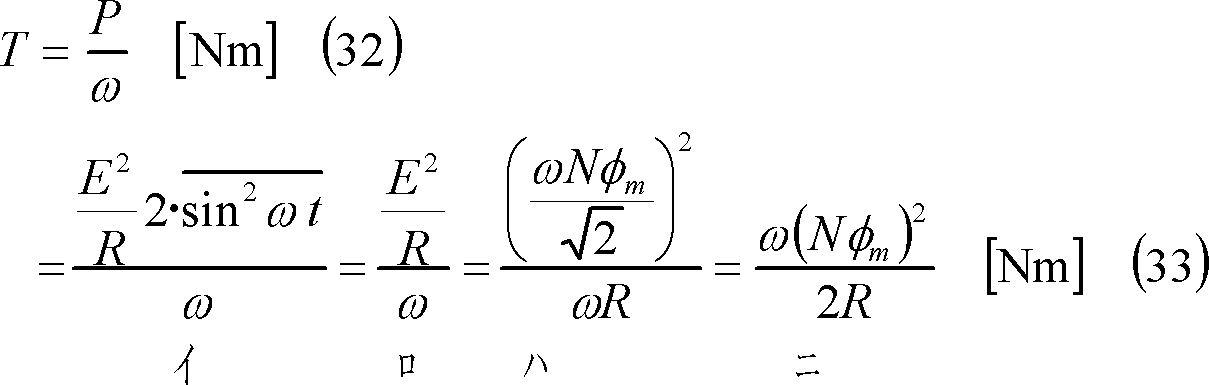
(10) 駆動トルク コイルを回転速度ωで反時計方向に回転させるためには、このトルクと同じ値の駆動トルクを外部から反時計方向に与えることが必要であり、駆動トルクTD(平均値)は、
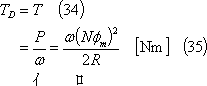
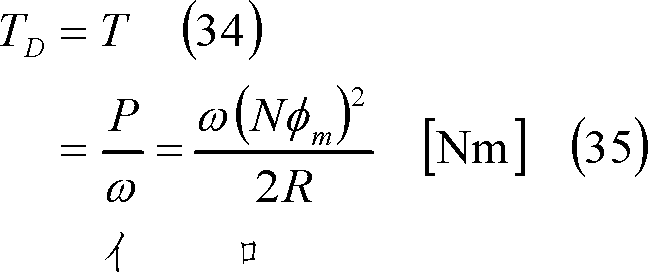
となる(⑧)。
(11) 考察 この場合の発生電力pは、(12)式の関係から、
であり、「pはRで消費される電力に等しい」ことがわかる。つまり、コイルをある回転速度で回転させる(駆動する)ことは、駆動トルクTDと同じ値の反抗トルクTが必要であり、このTをコイルに抵抗を接続することによって流れた電流によって作りだしている、ということができる。
第3図において、コイル端に抵抗と自己インダクタンスが直列に接続された場合について考えてみよう。
第4図 磁界中で回転するコイル ―その2―
(1) 第4図において、コイルを角速度ω[rad/s]で反時計方向に回転させると、コイルの誘導起電力eは①であり、ここで、
![]()
![]() とおけば、eは次式となる。
とおけば、eは次式となる。
(2) 回路の抵抗がR[Ω]、インダクタンスがL[H]であれば、コイルを流れる電流は②で、次式となる。
ただし、
![]()
![]()
ここで、電流の実効値をIとすれば、
(3) これによってコイルで発生する電力の瞬時値pは③となり、その平均値Pは④であり、これらを式で示せば次のようになる。
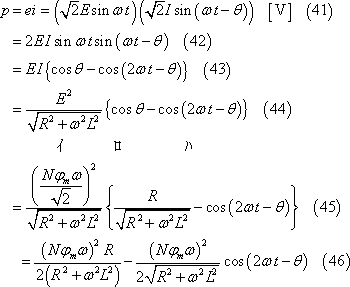
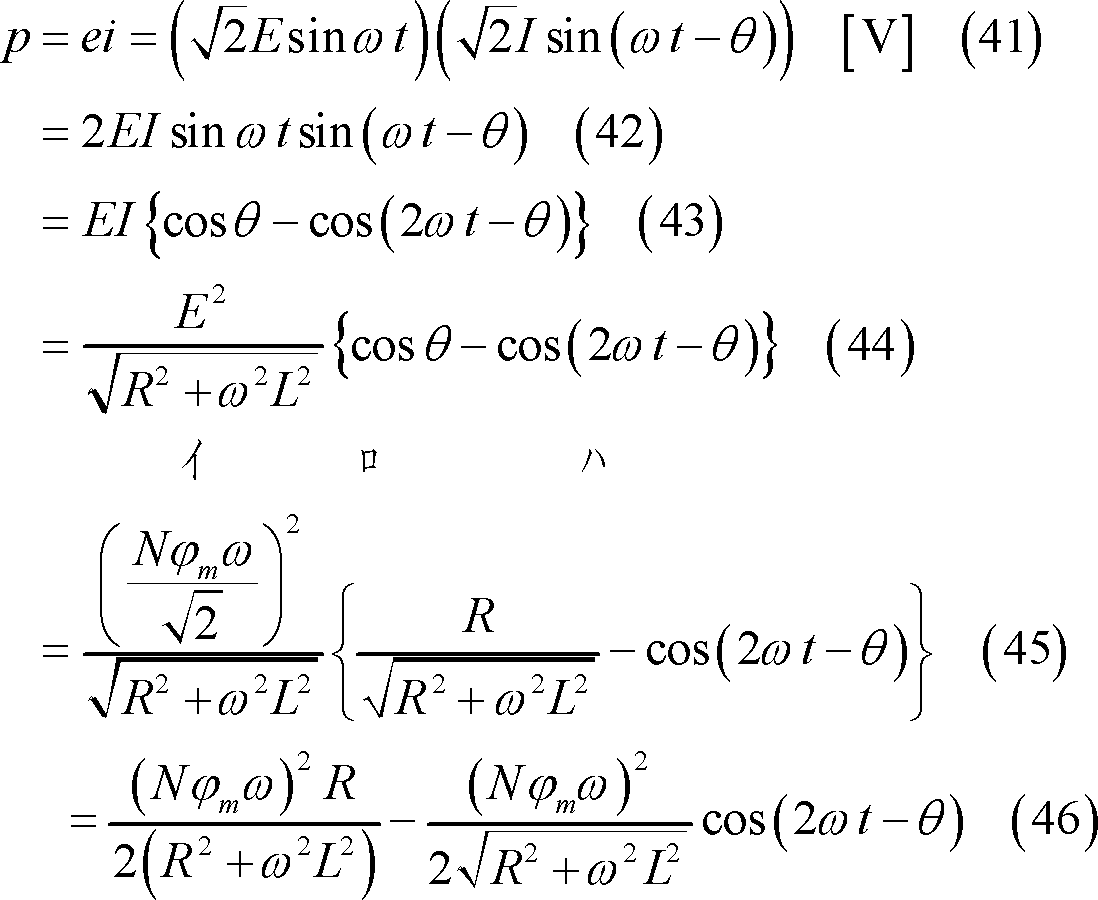
pの平均値(平均電力)Pは、
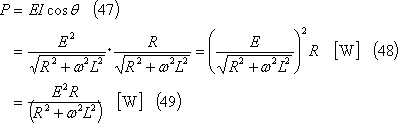
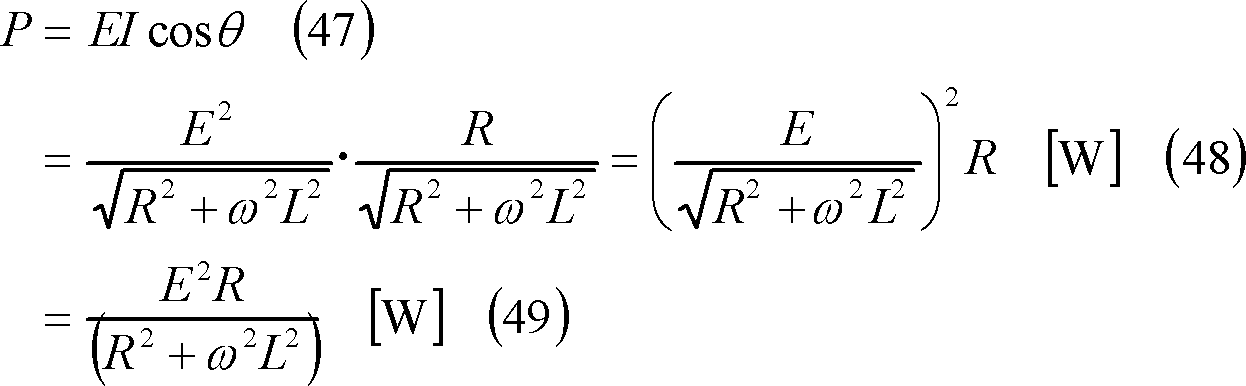
この結果から、Pは「Rで消費される熱エネルギーI2Rに等しい」ことがわかる。
(4) この電流によってコイルに発生するトルクτは⑤、平均トルクTは⑥となり、Tは次式で示される。
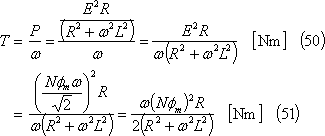
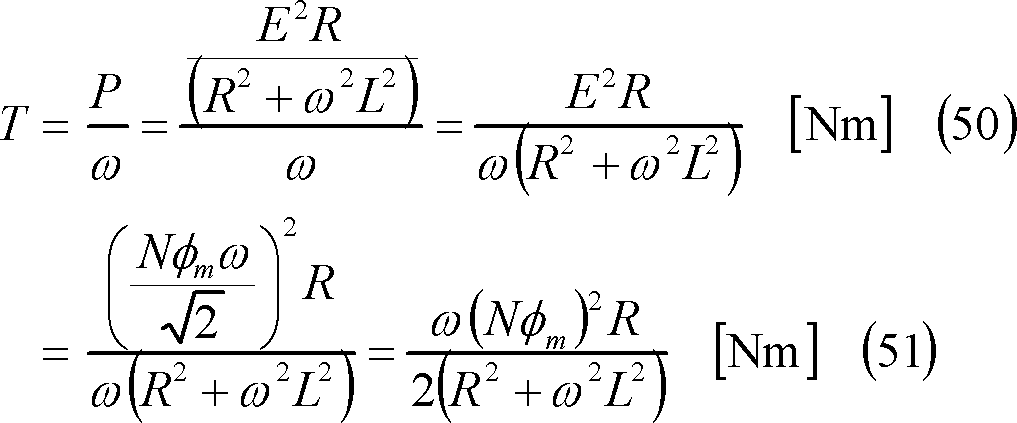
(5) トルクτは、電力pと同様に、次式のように、平均トルクτ1と変動(交番)トルクτ2に分解して考えることができる。τ、τ1、τ2は波形で示すと⑦となる。
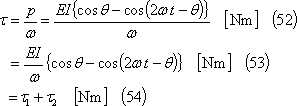
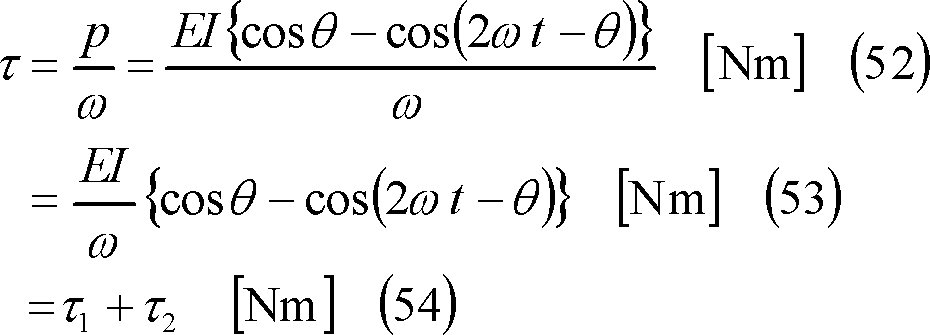
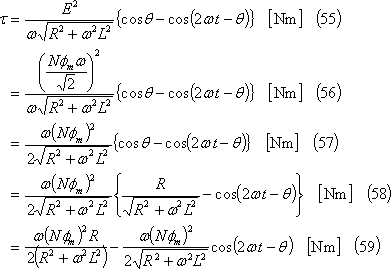
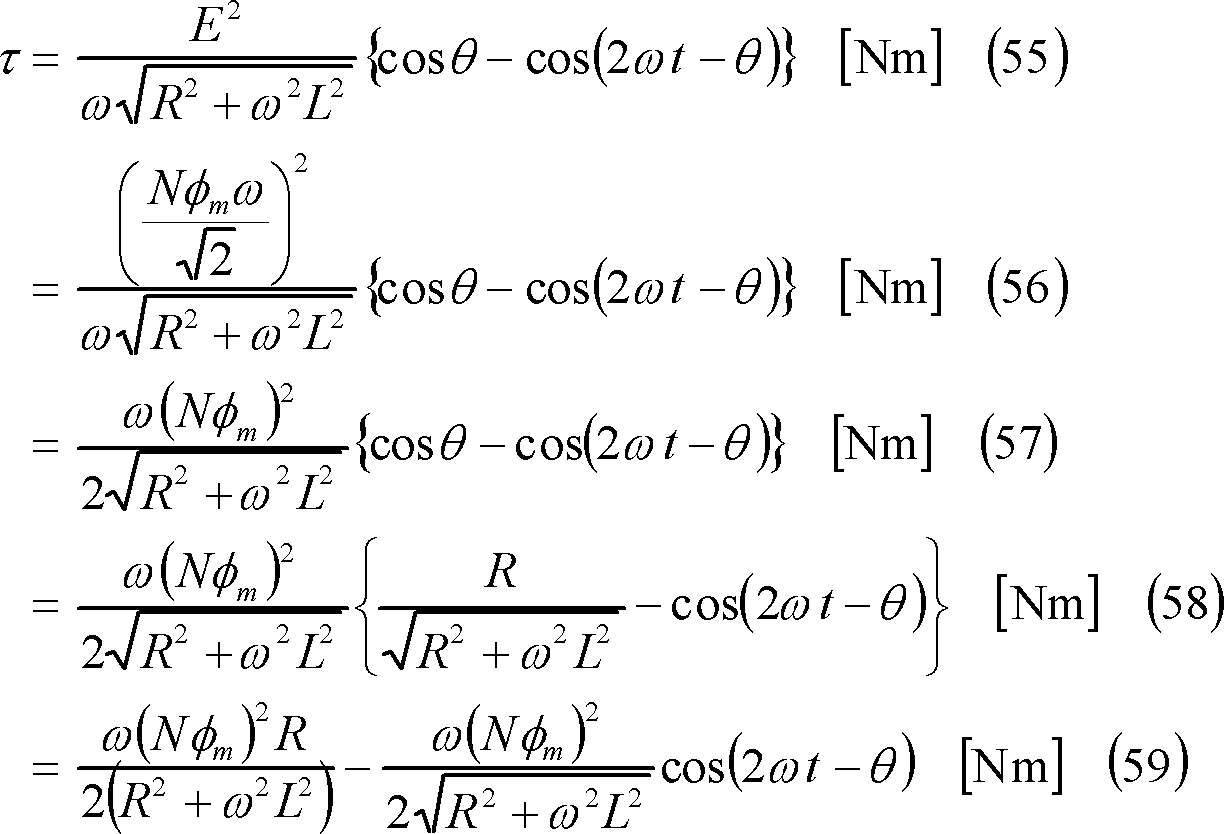
(6) トルクの性質 この場合の平均トルクは、(51)式で示されるので、次式のように変形できる。この結果、Tはωによって第5図のように変化することがわかる。
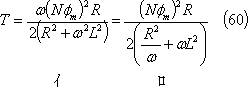
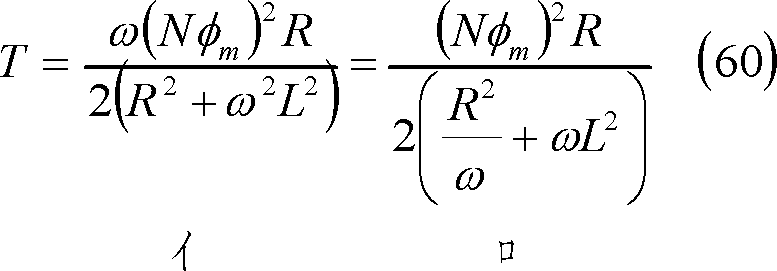
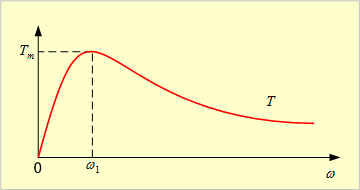
第5図 トルクTのωに対する変化
(1)動力の計算式 直線運動 ・・・・・・第1図、(3)式。
回転運動 ・・・・・・第1図、(6)式。
(2)交流起電力の発生と回転動力との関係。
(3)(2)とインダクタンスとの関わり。
