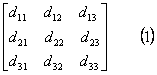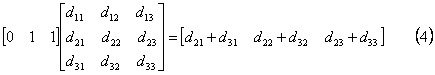第1図のように発電機端でb相端子Bとc相端子Cとが短絡したときの各相の電流と電圧を求めてみよう。
ただし、発電機端子A、B、Cにおいて各端子の大地に対する電圧を![]() とし、各端子における図示の方向の電流を
とし、各端子における図示の方向の電流を![]() とする。また、発電機端子から電源側をみた正相、逆相、零相の各インピーダンスは
とする。また、発電機端子から電源側をみた正相、逆相、零相の各インピーダンスは![]() であるとする。これらは以後の回路についても特に断らない場合は同じものとする。
であるとする。これらは以後の回路についても特に断らない場合は同じものとする。
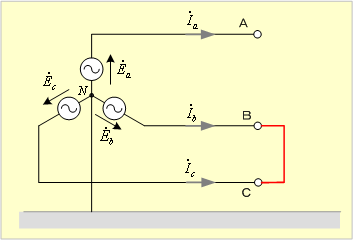
第1図 二相短絡回路(1)
*** 1 回路条件 ******************************************
![]()
*** 2 対称分変換 ****************************************
回路条件を対称分変換式へ代入する。電圧は、
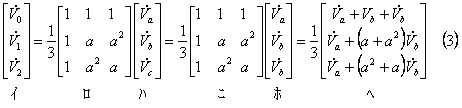
(3)式の右辺第2行と第3行は等しいので、
![]()
が成立する。同様に電流の回路条件を対称分変換式へ代入すると、
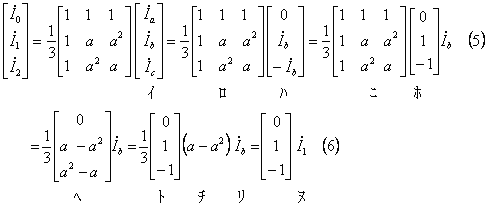
となり、(6)式の第1行から、
![]()
(6)式の両辺について、第2行と第3行を加えると、
![]()
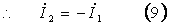
[補足説明](4)、(8)両式は行列により次のように計算することもできる。
| ☆ 行列の性質 ☆ 「行列の同一列の行同士を加減する方法」
上のような行列D があるとき、D に
となる。つまり、このような行列を左乗することで、同一列の行同士を加えた値を要素とする行列を作ることができる。
|
したがって、この性質を利用すると、(4)、(8)両式は次のように計算できる。すなわち、(3)式の両辺に![]() を左乗すると、
を左乗すると、
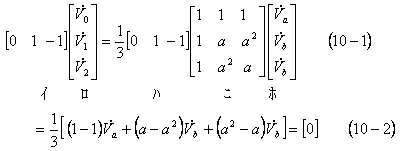
となり、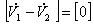
つまり、![]() なので、(4)式が得られる。
なので、(4)式が得られる。
また、電流の対称分変換式である(6)式から(8)式を導き出す場合も、(6)式の両辺に![]() を左乗すると、
を左乗すると、

![]()
となって、(8)式の ![]() が得られる。 (補足説明 終わり)
が得られる。 (補足説明 終わり)
*** 3 対称分回路計算 ***********************************
次に発電機回路との関連付けを行う。このため、(4)式に発電機の基本式を代入すると、
![]()
となり、上式を整理すると、次式が成立する。
![]()
上式のことを以後、対称分電圧方程式あるいは単に電圧方程式と呼ぶことにする。
電圧方程式である(13)式より、![]() は次式となる。
は次式となる。
![]()
![]() は、次のように「回路」から求めることもできる。
(7)、(4)、(9)式の3式から二相短絡回路(1)の対称分回路は第2図となることが分かる。
は、次のように「回路」から求めることもできる。
(7)、(4)、(9)式の3式から二相短絡回路(1)の対称分回路は第2図となることが分かる。
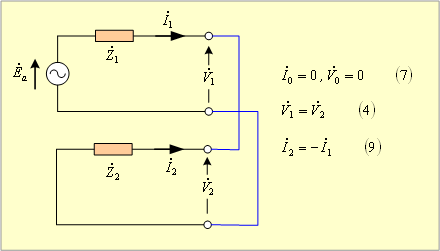
第2図 二相短絡回路(1)の対称分回路
したがって、第2図より![]() は(14)式となる。
は(14)式となる。
この結果、対称分電流は次式となる。
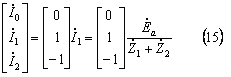
*** 4 逆変換 *******************************************
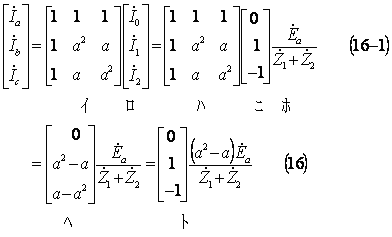
各相の電流は、電流の逆変換式に、3で求めた対称分電流((15)式)を代入して、次式で求まる。
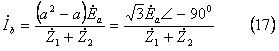
![]()
なお、![]() は
は![]() 関係を利用して、(17)式から直接(18)式を導くこともできる。
各相の電圧は交流発電機の基本式である
関係を利用して、(17)式から直接(18)式を導くこともできる。
各相の電圧は交流発電機の基本式である
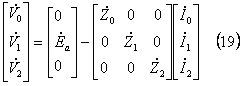
を、次のように逆変換して(21)式を得る。
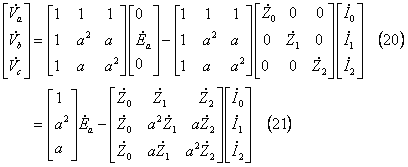
(21)式は 「対称分電流を代入すると、端子電圧が直接求まる式」 なので、この式に(15)式の値を代入して計算すると、
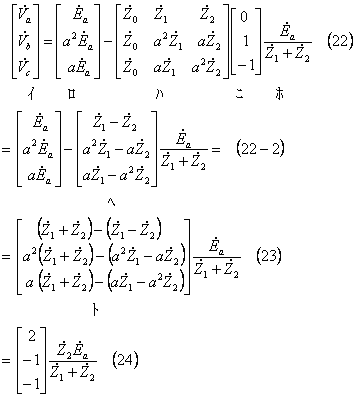
となり、この結果から、各相の端子電圧は、
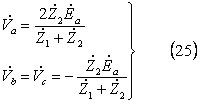
となる。
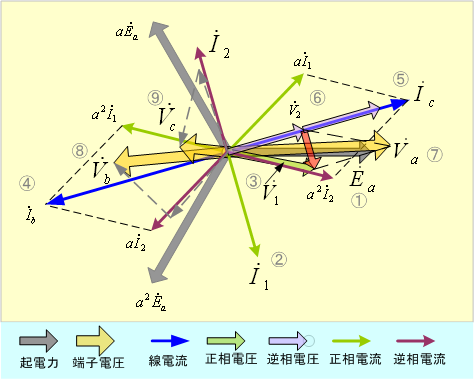
以上の内容をベクトルを使って表してみると、第3図のようになる。
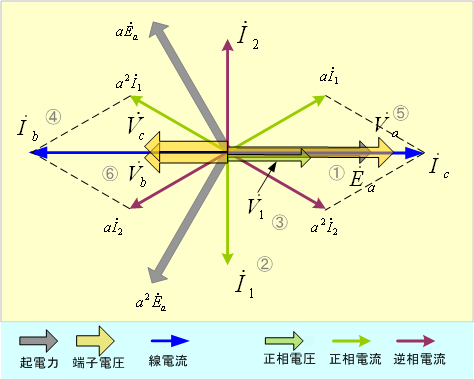
第3図 二相短絡回路(1)のベクトル図
問題1. 第1図の回路で、直接短絡する端子がB端子とC端子ではなく、A端子とB端子であった場合について、a相電流、b相電流及びa、b、c端の電圧を求めよ。
(答は巻末)
第4図の回路でb相端子とc相端子とが抵抗R を通して短絡したときの各相の電流及び電圧を求めてみよう。
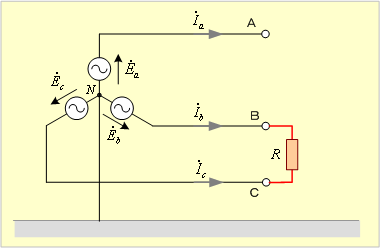
第4図 二相短絡回路(2)
*** 1 回路条件 *******************************************
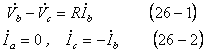
*** 2 対称分変換 ******************************************
電流の対称分変換は電流の回路条件が前に扱った二相短絡回路(1)と同じなので、(6)式と同じ計算となり次の2式となる。
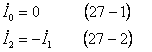
なお、この場合も
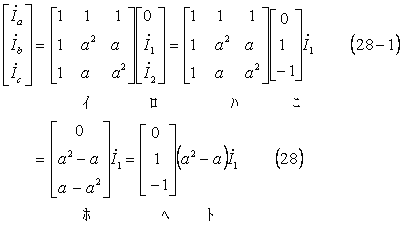
電圧の対称分変換は対称分変換式へ回路条件を入れ、更に対称分で表した電流((28)式)を代入して、次のように計算できる。
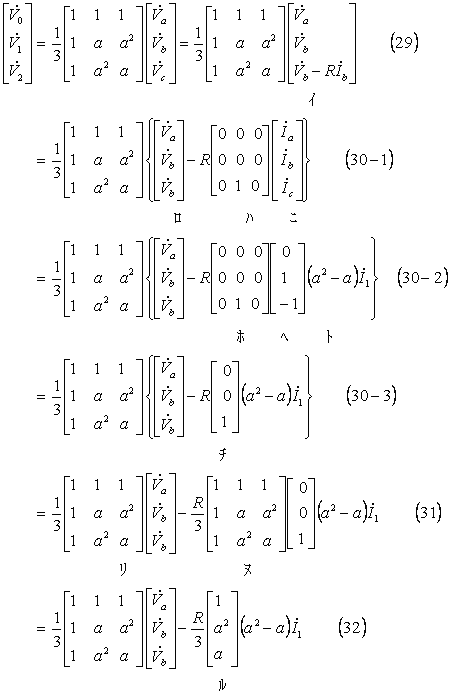
この結果、(32)式で第2行から第3行を引くと、
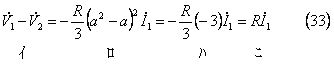
となり、次の式が成立する。
![]()
*** 3 対称分回路計算 ***********************************
上式に発電機の基本式を代入すると、
![]()
となり、同式を整理すると、次の対称分電圧方程式が得られる。
![]()
(36)式で得られた対称分電圧方程式から電流 ![]() は次式となる。
は次式となる。
![]()
なお、二相短絡回路(1)と同様に ![]() は次のように「回路」から求めることもできる。
は次のように「回路」から求めることもできる。
すなわち、(27-2)、(34)両式はこの場合の対称分回路が第5図であることを示している。
したがって、第5図より![]() は(37)式となる。
は(37)式となる。
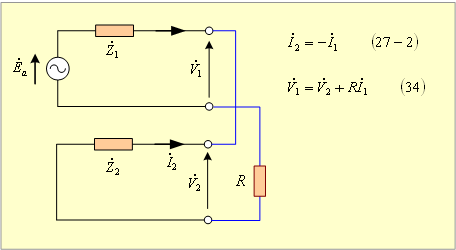
第5図 二相短絡回路(2)の対称分回路
電流の対称分((38)式の「イ」)は、同式「ロ」に等しいので、同式に(37)式の値を代入して、「ハ」となる。
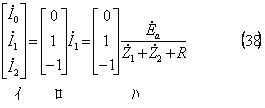
*** 4 逆変換 *******************************************
各相の電流は先に2の逆変換式で計算した結果である(28)式を利用し、同式に(38)式の ![]() を代入して次式となる。
を代入して次式となる。
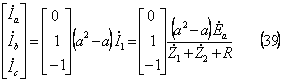
![]()
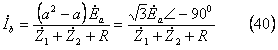
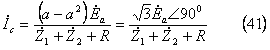
各相の電圧は「二相短絡回路(1)」で扱った(21)式を使用して求める。具体的には(42)式のように、(21)式の対称分電流のところに(38)式の値を代入すればよく、次のような計算となり、
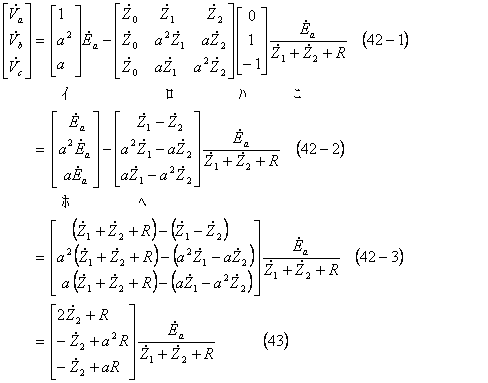
となる。
問題2. 第3図にならって、二相短絡回路(2)のベクトル図を描いてみよ。 (答は巻末) |
第6図の回路に示すようにa相端子とc相端子がそれぞれ抵抗Rを通してb端子と短絡したときの各相の電流及び電圧を求めてみよう。
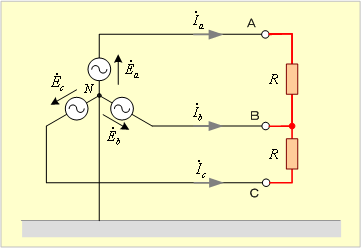
第6図 二相短絡回路(3)
*** 1 回路条件 *****************************************
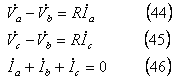
*** 2 対称分変換 *****************************************
まず、電圧及び電流の逆変換式を使用して、実回路量と対称分量との関係を明らかにするための式を用意しておく。この場合も(46)式より ![]() なので、
なので、![]() 、「零相回路はない」ので、その関係式は次式となる。
、「零相回路はない」ので、その関係式は次式となる。
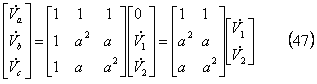
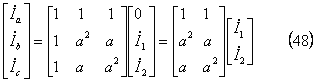
電圧の対称分変換は、対称分変換式に回路条件等を取り入れることで求められ、(49-1)式のように計算を進める。
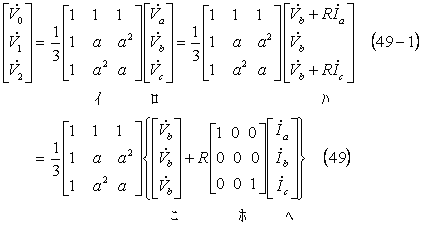
つまり、上式のように右辺第1項(電圧項)と第2項(電圧降下項)とに分けて表すことにする。そして更に第2項に対称分で表した電流((48)式)を代入して、
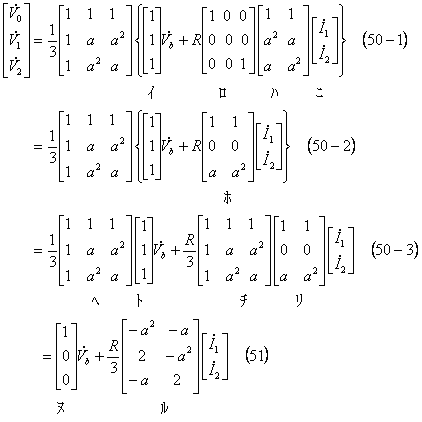
となる。この結果、(51)式の第2行と第3行に注目すると、次式が成立する。この式が発電機端子より外(R)側における対称分電圧と電流の関係を示す関係式である。
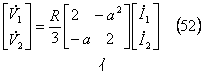
[補足説明](49-1)式の計算のように、電圧行列Vが V=VK-ZI であるとき、Vの対称分変換V ’は、変換行列をCとすれば、次のように計算できる。
V ’=C(VK-ZI )=CVK-CZI=CVK-CZ(C-1I’)=CVK-(CZC-1)I’(53)
=VK’-Z’ I’ (54)
なお、ここで、Z’=CZC-1 であり、Z’はZ の対称分変換されたインピーダンスということができる。
先に行った電圧の対称分変換作業である(49-1)~(51)式への式変化は、このような背景の下で行われたもので、(50-3)式右辺第2項の「リ」は、上式 V ’=・・・=CVK-(![]() )I’ の下線部(Rを除いたもの)を表しているのである。
)I’ の下線部(Rを除いたもの)を表しているのである。
(補足説明終わり)
*** 3 対称分回路計算 *****************************************
次に発電機回路との関係を調べてみよう。零相回路がない場合の発電機の基本式は、
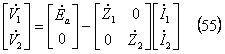
となるから、(52)式と(55)式を等値して、次式が成立する。
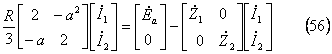
上式を(57)式のように整理して、
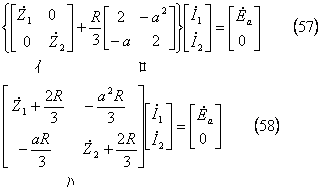
が得られる。この式が短絡回路(3)における対称分電圧方程式である。
電流の対称分は(58)式を電流について解けばよく、次式となる。
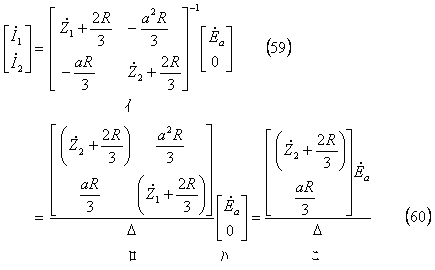
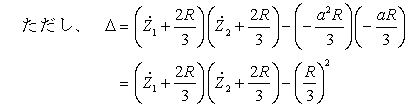
*** 4 逆変換 *****************************************
電流は電流の逆変換式でも求まるが、ここでは(48)式を利用することにして
次のように計算し、
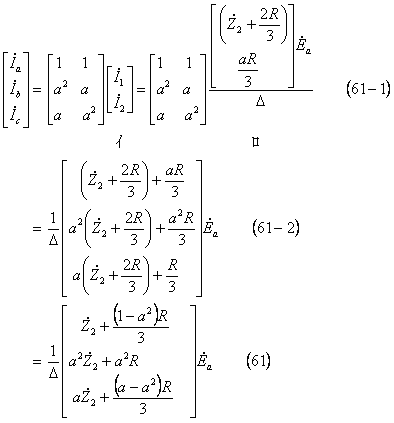
となる。
また、電圧も同様にして、(47)式を利用することにして、(47)式に(52)、(60)式を代入して次のように求まる。
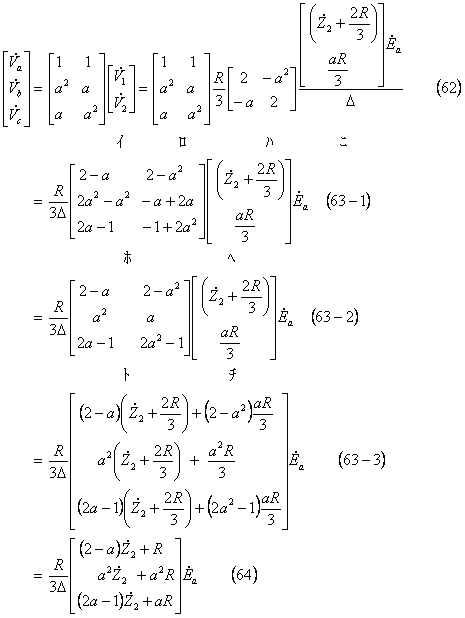
なお、上式中の![]() は(60)式のただし書きにある
は(60)式のただし書きにある![]() と同一のものである。
と同一のものである。
第7図の回路に示すようにA、B、Cの3端子が抵抗Rを通して短絡したとき(三相短絡回路)の各相の電流と電圧、及び短絡点Sの対地電圧(電位)を求めてみよう。
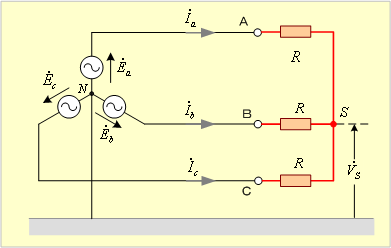
第7図 三相短絡回路
*** 1 回路条件 *****************************************
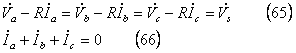
(65)式を電流について行列で表示すると、
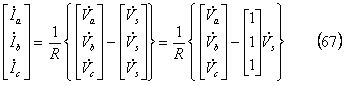
上式の両辺に、![]() を左乗すると、
を左乗すると、
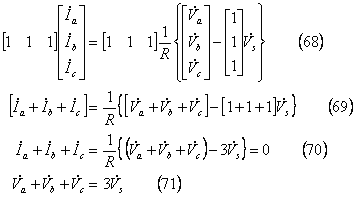
![]() なので、
なので、![]() 。この結果、(67)式は次式となる。
。この結果、(67)式は次式となる。
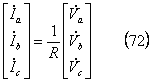
*** 2 対称分変換 *****************************************
(72)式を対称分で表示すると、
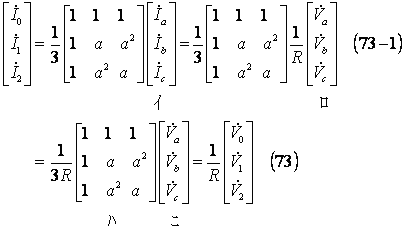
となる。しかし、零相回路がない場合は次式で扱ってよく、(74)式が得られる。
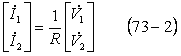
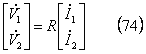
*** 3 対称分回路計算*****************************************
ここで、(74)式を発電機の基本式と等値すると、次式となる。
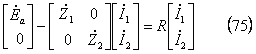
(75)式を(76)式のように整理し(77)式が得られる。
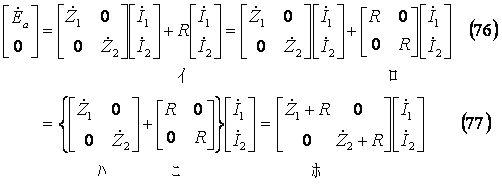
(77)式が発電機回路を含めた「対称分電圧方程式」である。
上記の電圧方程式を電流の対称分![]() について解けば、
について解けば、
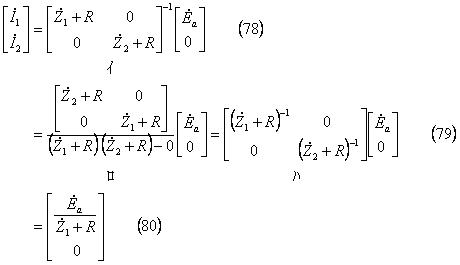
となり、電流 ![]() は次式となる。
は次式となる。
![]()
(80)式は ![]() であることを示し、対称分回路が正相回路だけであることを示している。したがって、三相短絡回路の対称分回路は第8図となる。
であることを示し、対称分回路が正相回路だけであることを示している。したがって、三相短絡回路の対称分回路は第8図となる。
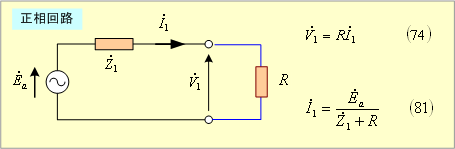
第8図 三相短絡回路の対称分回路
*** 4 逆変換 *******************************************
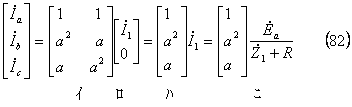
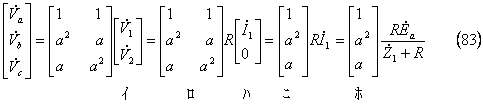
[参考]電圧の求め方(別計算) 電圧は次式のように求めることもできる。
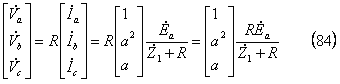
(1)回路条件 電圧、電流、電圧と電流の相互関係を調べ、その結果を式で表示する。
(2)対称分変換 (1)の結果を対称分に変換して、対称分量相互の関係を知る。
(3)対称分回路計算
① (2)で得られた関係に発電機回路の内容を加え、
電圧に関する方程式にまとめる。この式を対称分に関する「電圧方程式」と呼ぶ。
② 電圧方程式や関係式をもとに、対称分量を導出するか、
対称分回路を作成し、同回路から対称分量を計算で求める。
(4)逆変換 (3)で得られた対称分量を逆変換して、求めていた実回路量を知る。
------------------------------------------------------------------
[問題1の答]
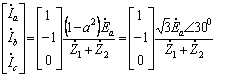
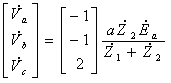
[問題2の答]
第9図 二相短絡回路(2)のベクトル図