〜終わり〜
■ぜひアンケートにご協力下さい■


(参照:=理論一般= 基礎・解説コース「インダクタンス物語(7)」)
(1)磁界中でコイルを回転させる
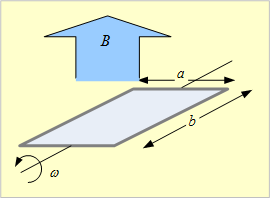
第1図 磁界中でコイルを回転させる
「インダクタンス物語(7)」で学んだように、a[m]、b[m]を辺とした巻数Nの長方形コイ
ルを第1図のように配置して、回転させてみる。
第2図の①のボタンのように、磁束密度Bの平等磁界中で回転角速度ω[rad/s]で反時計方向に回転させると、時刻tにおける鎖交磁束は、
![]()
![]() となるので、コイル端には次式で示す起電力eが誘導される。
となるので、コイル端には次式で示す起電力eが誘導される。
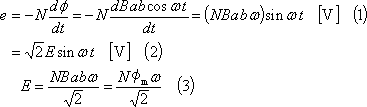
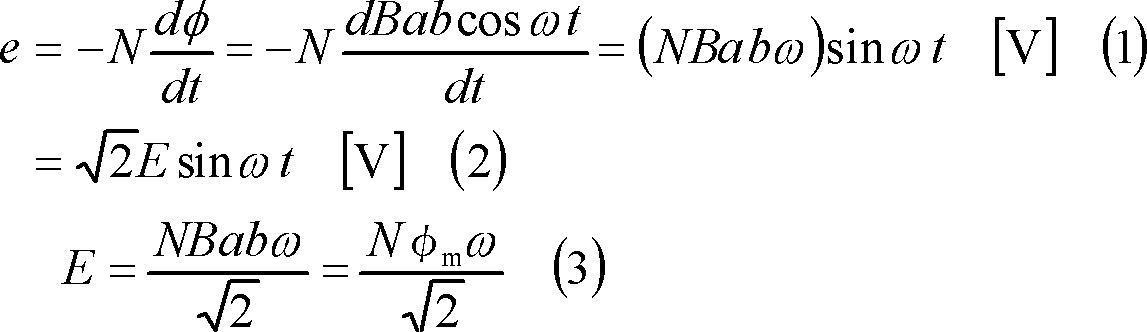
第2図 コイルにトルクを発生させる
(2)静止コイルの周囲で磁界を回転させる
次に、②の左ボタンのように、コイルを静止した状態に置き、平等磁界Bをω[rad/s]で時計方向に回転させると、時刻tにおけるコイルの位置は②の中ボタンの位置となるので、鎖交磁束は、
となり、②の右ボタンのように、コイルには、(1)式と同じ起電力eが誘導される。
したがって、コイル端に抵抗と自己インダクタンスを接続すると、回路の抵抗がR[Ω]、自己インダクタンスがL[H]であれば、コイルには次式の電流iが流れる(③のボタン)。
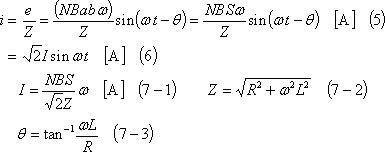
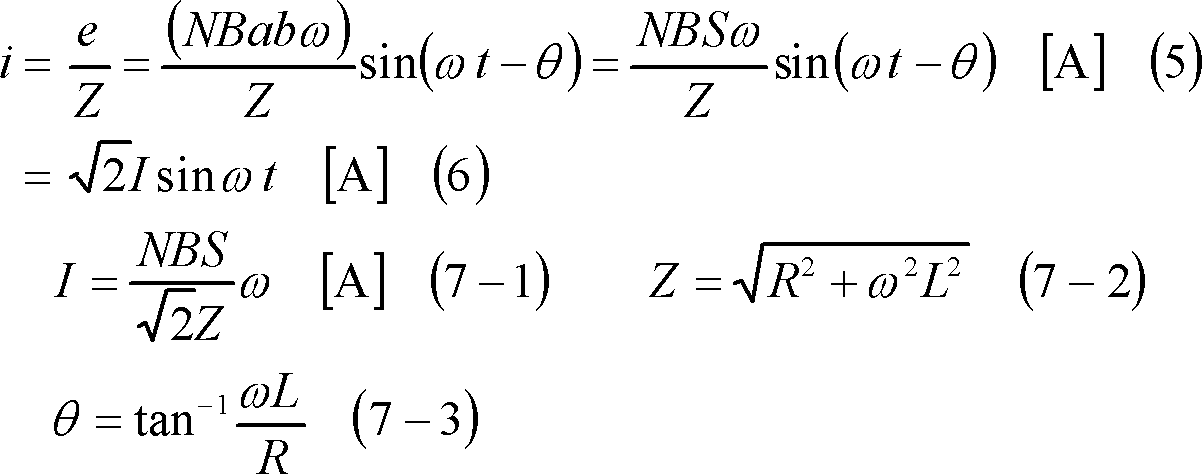
この結果、コイルのb辺にはこの電流iと磁界Bにより、④の左ボタンで示す電磁力fbが働き、この力は時計方向の回転力τ(トルク)をつくり、④の右ボタンのように変化する。ここで、瞬時電力p(=ei)と平均電力P((8)式)は画面(⑤の左ボタン)のようになり、トルクとは、(9)式の関係にあるので、トルクTは(9)式、(10)式、その波形は⑤の右ボタンのようになる。
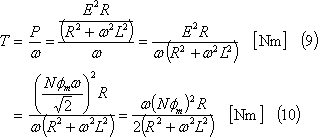
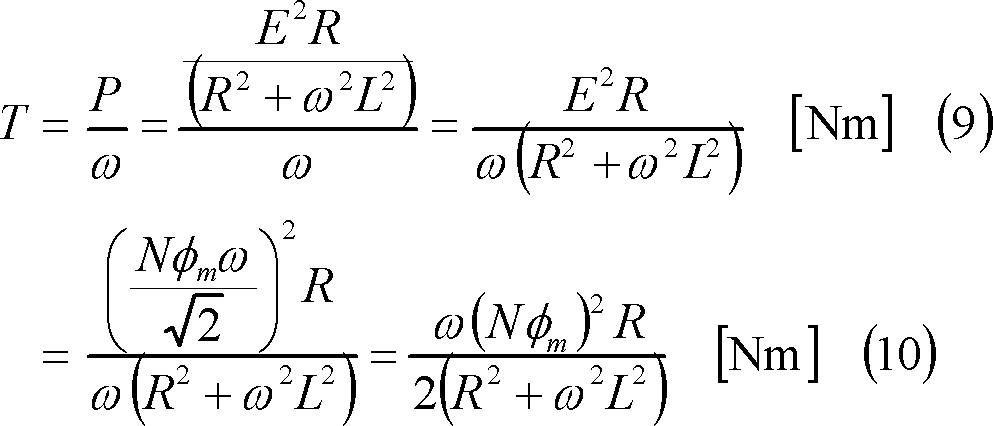
以上の結果から、コイルにはトルクが発生するので、コイルの軸に回転負荷を接続すれば、コイルは回転負荷を駆動することができ、電動機として機能することになる。
(参照:=理論一般= 基礎・解説コース「回転磁界の仕組み」)
(1)回転磁界の基礎(交番磁界と複数コイルによる磁界)
第3図において、X軸方向を軸とするAコイルに電流を流したときにできる磁界について考えてみる。このコイルの断面を①-1ボタンのように表し、①-2ボタンのように電流を流した時、コイルを図のような方向の電流が流れるものとする。ここで、コイルに、①-3ボタンの(b)図に示す正弦波交流iAを流すと、コイル中心部の磁界(A軸磁界)hAは同図下段のように電流に比例し、時間に対し正弦波状の変化をする。これをベクトルで示すと、①-4ボタンの(a)図のようになる。この結果、この磁界は交番磁界であることがわかる。
次に、②-1ボタンのように、Aコイルと同じ仕様のBコイルを同心円状に90°時計方向の位置に配置し、AコイルにiAを流すと、その磁界、つまり、A軸磁界hAのグラフは②-2ボタンとなる。このグラフからわかるように、これからは図のように、磁界ベクトルを該当時刻の時間軸上に表すこともある。
ここで、②-3ボタンのように、BコイルにiAと同相、同大の電流iBを流すと、その磁界hBのグラフとベクトルは(c)図となるから、両軸磁界のベクトルは(d)図となり、その合成磁界は(a)図の茶色のベクトルで示される。この結果、合成磁界はA軸磁界より45°B軸よりの方向を軸とする交番磁界となることがわかる。
次に、③-1ボタンで両電流の大きさが違うとどのような磁界となるが観察してみよう。画面右下のコントロールバーによればiBのiAに対する値を変更できる。現在は茶色のバーが目盛零となっているので、iBは流れていない。バーをマウスで左ドラッグして100の目盛に移すと、iBはiAと同相同大となるので、磁界は②-3ボタンの場合と同じ磁界となる。以後、バーをいろいろな位置に移動してどのような磁界ができるか、観察してみよう。
この場合の磁界は、次式のように表すことができる。したがって、両磁界の大きさを変えることで、いろいろな大きさで、いろいろな方向の交番磁界が作れることがわかる。
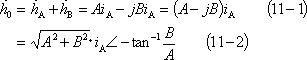
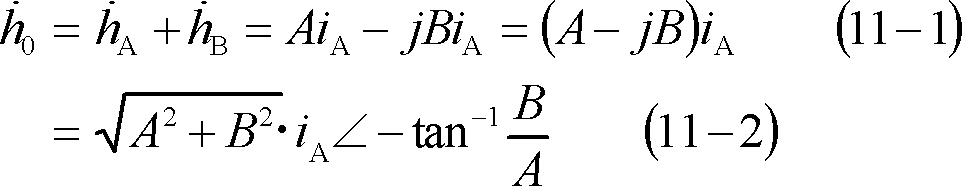
【問題1】 第3図において、iBをiAの50[%]の大きさとしたとき、磁界の大きさはiAのそれの何倍となるか。また、磁界の軸方向はどの方向となるか。
次に、iBをiAと同じ大きさで、iAに対して位相を遅らせてみよう。③-2ボタンの画面右下のコントロールバーで、いろいろな位相について観察してみよう。
観察の結果は、θBが小から次第に大きくすると、ベクトルの先が左上と右下の方向が長径の楕円軌道を描き、次第にふくらみをもつ楕円軌道を描く。θBが180°から次第に減少させると、右上左下が長径の楕円がふくらみを増し、90°で円軌道となることがわかる。
つまり、③-3ボタンで示すように、Bコイルを流れる電流がAコイルの電流と同じ大きさで、位相を90°遅らせると、大きさが1軸磁界と等しく一定で、一周期で1回転する回転磁界となる。これが「二相交流がつくる回転磁界」である。
第3図
(2)回転磁界の仕組み
それでは、どのようにしてこのような回転磁界ができるのか、調べてみよう。
④-1ボタンで(d)図に示すように、大きさが一定で1周期で1回転するベクトルのことを回転ベクトルと呼ぶことにする。そして、図のように回転方向が時計方向の場合をh1とすると、h1は(c)図に示す時間的変化をする。また、④-2ボタンのように、h1と大きさが同じ回転ベクトルで反時計方向に回転する回転ベクトルをh2とすれば、h2は(f)図の時間的変化をする。そこで、h1とh2を④-3ボタンのように相対しておくと、その合成値hAは(d)図となる。つまり、(b)図のiAがつくる交番磁界hAは、(a)図と(c)図で示されるが、これは(d)図のようにh1とh2の合成に等しく、「一つの交番ベクトルは二つの回転ベクトルに置き換えて表す」ことができる。グラフ上では(d)、(e)、(f)の各図の関係となる。これらの関係は次の(12)式に示す。
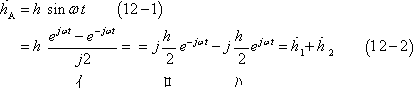
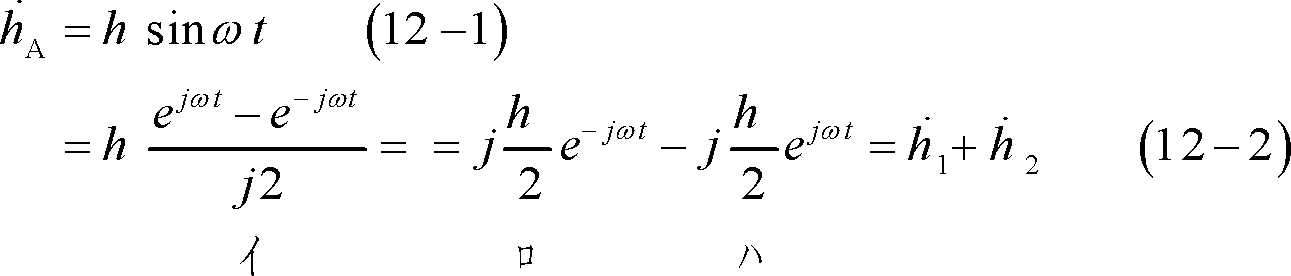
この結果、二相交流の回転磁界は④-4ボタンで(b)図のグラフで示すように、A軸磁界hAを表す(c)図に対して、B軸磁界hBは、Aコイルより90°空間的にずれた位置で、iAより90°位相の遅れた電流を流すことで、(e)図のように位相が90°の時、回転ベクトルの起点が来るようなタイミングとなるので、(c)、(e)図を対比するとわかるように、両磁界のh1は常に同じ方向を保ちながら時計方向に回転し、h2は常に打ち消し合うので、結果として(a)図のように2h1の回転磁界となるわけである。
(3)三相交流の回転磁界
次に、三相交流の回転磁界の作り方について調べてみよう。
まず、⑤-1ボタンのように、同一仕様の3個のコイルABCを図のようにAコイルから空間的に時計方向に120°毎にずらして配置する。これらの3個のコイル全てに電流iAを流すと、3軸の磁界hA0、hB0、hC0は(c)図となり、その合成は零となり磁界はできない。ちなみにこれらの磁界を回転ベクトルで表すと、⑤-2ボタンの(c)図となる。
次に、⑤-3ボタンのように、BコイルにiAより120°遅れた電流を流すと、B軸磁界hBは(e)図のように、B軸で位相120°の時刻を起点とした交番ベクトル(緑)となる。また同様に、CコイルにiAより240°遅れた電流を流すと、C軸磁界は位相240°が交番ベクトルの起点となる交番ベクトル(青)となり、これら3軸磁界の合成値は(a)図となり、一周期で1回転する回転磁界となる。⑤-4ボタンの(c)図は、これらの関係を回転ベクトルで表したものであるが、これらの図からわかるように、各瞬時について、h1は3軸とも同方向なので3h1となり、h2は互いに打ち消し合って消滅しており、全体としての合成磁界は、1軸当たりの磁界の大きさの3/2倍の大きさで時計方向に回転している磁界であることがわかる。
したがって、A軸電流より順に120°位相の遅れた電流を3個のコイルに流すと、『大きさが1個のコイルがつくる磁界の1.5倍で一定で、電流1周期で1回転する』回転磁界ができる。これらの関係を式でみると次のようになる。
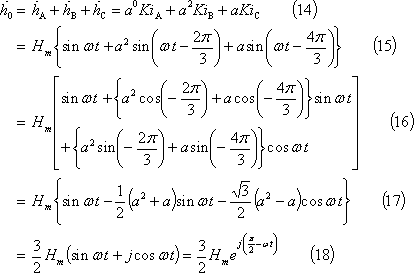
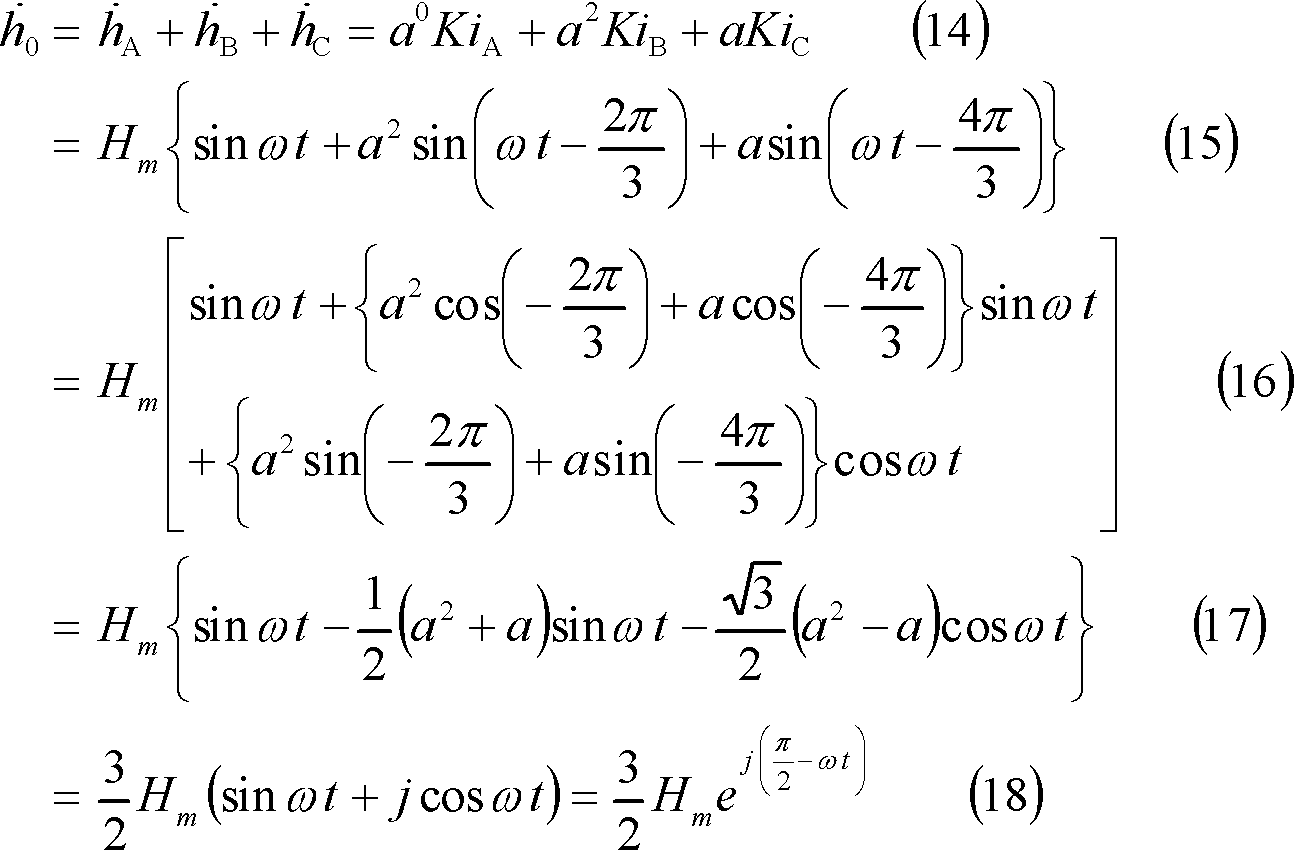
ただし、
![]()
![]()
[注]:⑤-5ボタンの内容は第4図②-3の次に、⑥ボタンの内容は6番で、それぞれ解説する。
(1)三相誘導電動機の発生トルク
第4図
三相誘導電動機の主要部分は、第4図に示す電動機の断面において、①のボタンのように、回転磁界をつくるためのコイルを納める固定子、固定子コイル、回転部分となる回転子、トルクを発生させるために回転子に納める回転子コイル、それに固定子と回転子間にある空隙である。
固定子コイル1個がつくる磁界は、②-1ボタンのようにコイルに(b)図のような直流電流Iを流した場合は、(a)図のような磁束分布となるように作られる。具体的には回転子コイルの軸方向の空隙部をG1とし、以下図のように空隙部の位置をG0、G1、G2、G3とそれぞれ表示すれば、空隙部の磁束の空間分布は(c)図のように、空隙に沿って正弦波状の分布となる。そこで、②-2ボタンのように紫線のところで固定子と回転子を切り離し、空隙部を中心として直線状に展開すると右の図のように、固定子と回転子で空隙をサンドイッチしたような形となり、固定子の空隙面に固定子コイルが配置されたようになる。したがって、②-3ボタンにおいて、さきほどのようにコイルに直流電流Iを流した場合の空隙部の磁束分布は(b)図であったが、(c)図のように交流を流したときは(d)図のような変化をすることになる。なお、(a)図の黄色円はこの部分の空隙が右の図のどの部分に相当するかを紫線で示したものである。
以上の結果から、固定子コイルに交流電流を流すと、空隙部という空間で交番的な磁束変化が起きることになる。
次に、③-1ボタンのように、固定子上に3個のコイルABCを空間的に120°毎回転した位置に配置し、そこに三相対称交流を流すと、先に解説したように3軸の磁界は(d)図となり、空隙部には(a)図茶色で示す回転磁界ができる。
[注]ここから、第3図⑤-5ボタンの説明に戻る。
3個の固定子コイルから構成される三相誘導電動機の場合は、これらのコイルに三相対称交流を流すと、第3図⑤-5ボタンを押すと現れる画面の(c)図のように、空隙上に3個の交番磁界hGA、hGB、hGC、が現れることになる。
いま、
![]()
![]() をβとおけば、空隙上でG0から距離xにおける磁界は(20-1)式で示されるから、(20-2)式のように表せ、この式から磁界は、時計方向に回転する正弦波分布磁界hGA1と反時計方向に同じ角速度で回転する正弦波分布磁界hGA2の和で表わされることがわかる。
をβとおけば、空隙上でG0から距離xにおける磁界は(20-1)式で示されるから、(20-2)式のように表せ、この式から磁界は、時計方向に回転する正弦波分布磁界hGA1と反時計方向に同じ角速度で回転する正弦波分布磁界hGA2の和で表わされることがわかる。
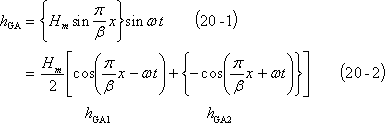
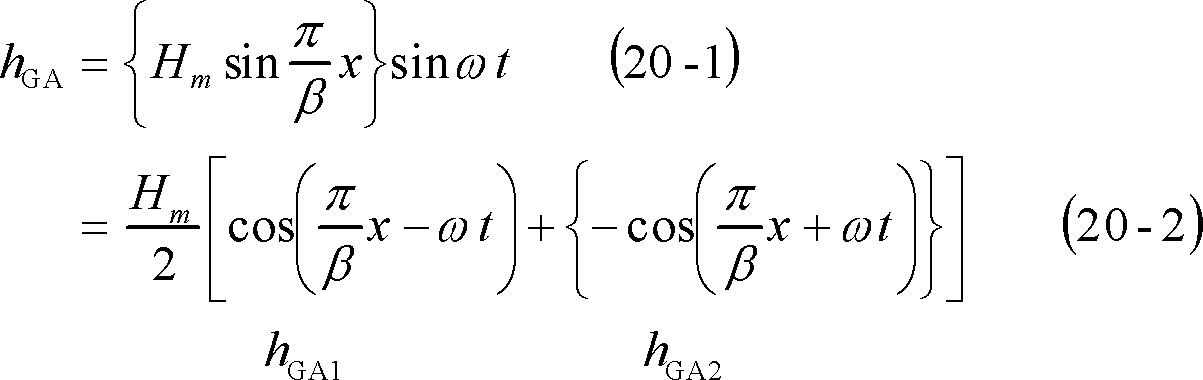
この結果、(c)図の各グラフでは、この場合の空隙における磁界の時間的変化の様子が観察でき、時計方向の回転磁界ができることがわかる。
[注]第4図③-2へ進む。
以上の結果をまとめて示すと③-2ボタンとなる。この画面の空隙部で磁束の粗密の状態が、また(c)図から、空隙部を正弦波状に空間分布した磁束が時間とともに右へ移動し回転している様子が、それぞれ確認できる。③-3ボタンは、③-2ボタン(a)図のように回転する磁束を実体図でなく、幅広の矢印で示す例をあげてある。なお、この画面で回転磁界の回転速度を調べてみると、回転磁界は、電流一周期で1回転しているのが確認できるので、電源周波数をf[Hz]とすれば、毎分60f回転していることになる。
以上の結果、固定子コイルによって④-1ボタンに示す回転磁界が作られることになる。
したがって、回転子コイルにはこの回転磁束が鎖交し時間とともに変化するので起電力が誘導される。この場合の鎖交磁束は(c)図φのように時間的に変化するため、この起電力eは、次式で求められ、画面では波形eとして表される。
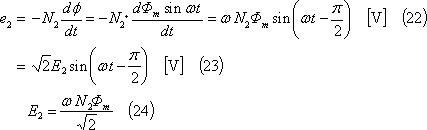
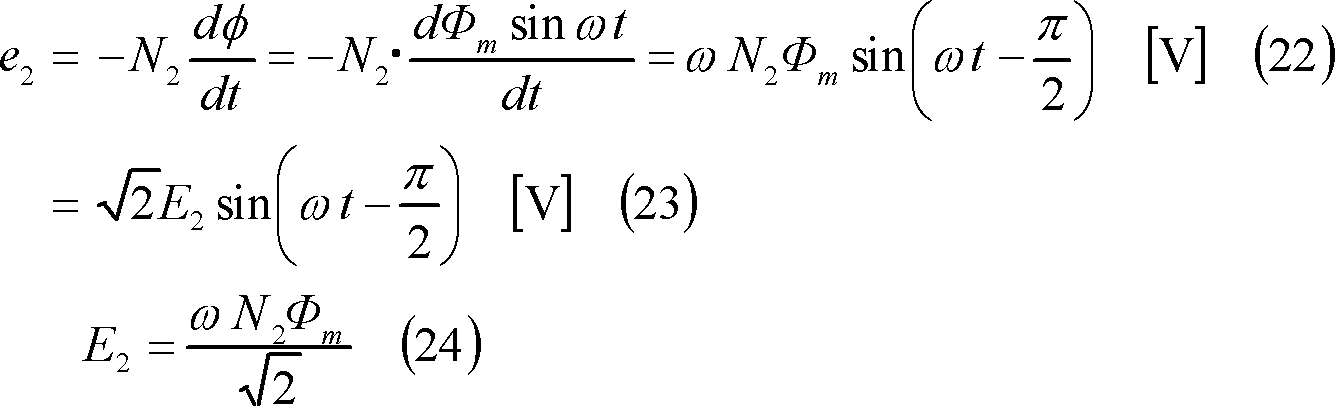
ここで、回転子コイル端を短絡すると、コイル内部の抵抗がr[Ω]、インダクタンスが
![]()
![]() [H]であれば、同コイルには(25)式で示す電流が流れ、この結果、コイルにはこの電流によってトルクτが発生する。これらの関係は④-2ボタンで観察できる。
[H]であれば、同コイルには(25)式で示す電流が流れ、この結果、コイルにはこの電流によってトルクτが発生する。これらの関係は④-2ボタンで観察できる。
回転子コイルでの消費電力P2は、
となり、すべてコイル抵抗rで消費する電力となり、熱に変換される。
一方、コイルに電流が流れたことによって、コイルには次式で示すトルクTが発生する。
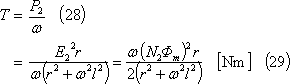
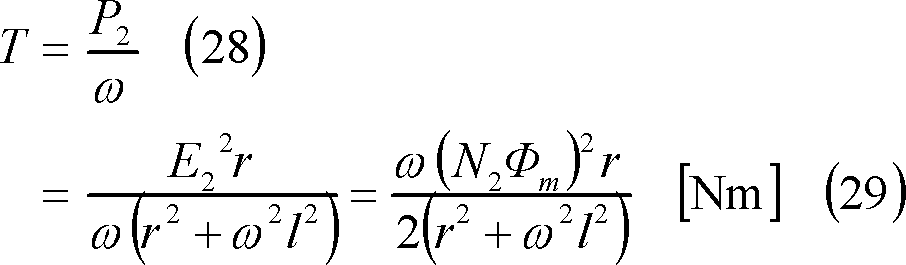
(2)回転子に負荷を接続すると
(29)式は、回転子が静止しているとき回転子に時計方向に働く駆動トルクである。したがって、回転子にトルクTの回転負荷が接続された場合は、この負荷トルクと等しい駆動トルクを電動機が発生することになる。
このとき回転子速度(電動機速度)をNR[min-1]とし、角速度をωR[rad/s]とする。
回転磁界の回転速度を同期速度と云い、NS[min-1]で表す。回転磁界は、電源の周波数をf[HZ]、極数をPとすれば、電流1周期で、(2/P)回転するので、
回転磁界の回転角速度
![]()
![]() は、
は、
回転磁界と回転子との回転速度の関係をすべりとして次のように定義する。
すべりは角速度についても成立し、次式となる。
電動機速度
![]()
![]() は、
は、
回転子の相対速度
![]()
![]() は、
は、
と表わせる。
第5図 回転磁界と回転子との関係
電動機に負荷が接続された場合、回転磁界と回転子コイルの関係は、第5図で、①のボタンを押すと現れる(a)図となる。回転子に乗って回転磁界をみると、②のボタンを押すと現れる(b)図となる。つまり、(b)図は相対速度の図であり、電動機トルクの式である(29)式のωは相対速度を指しているわけである。
この結果、トルクTは、次式のようになるので、
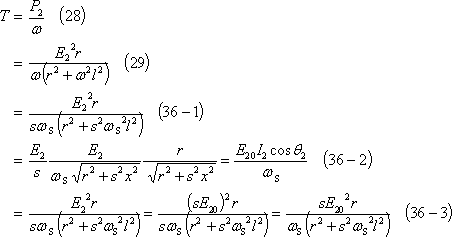
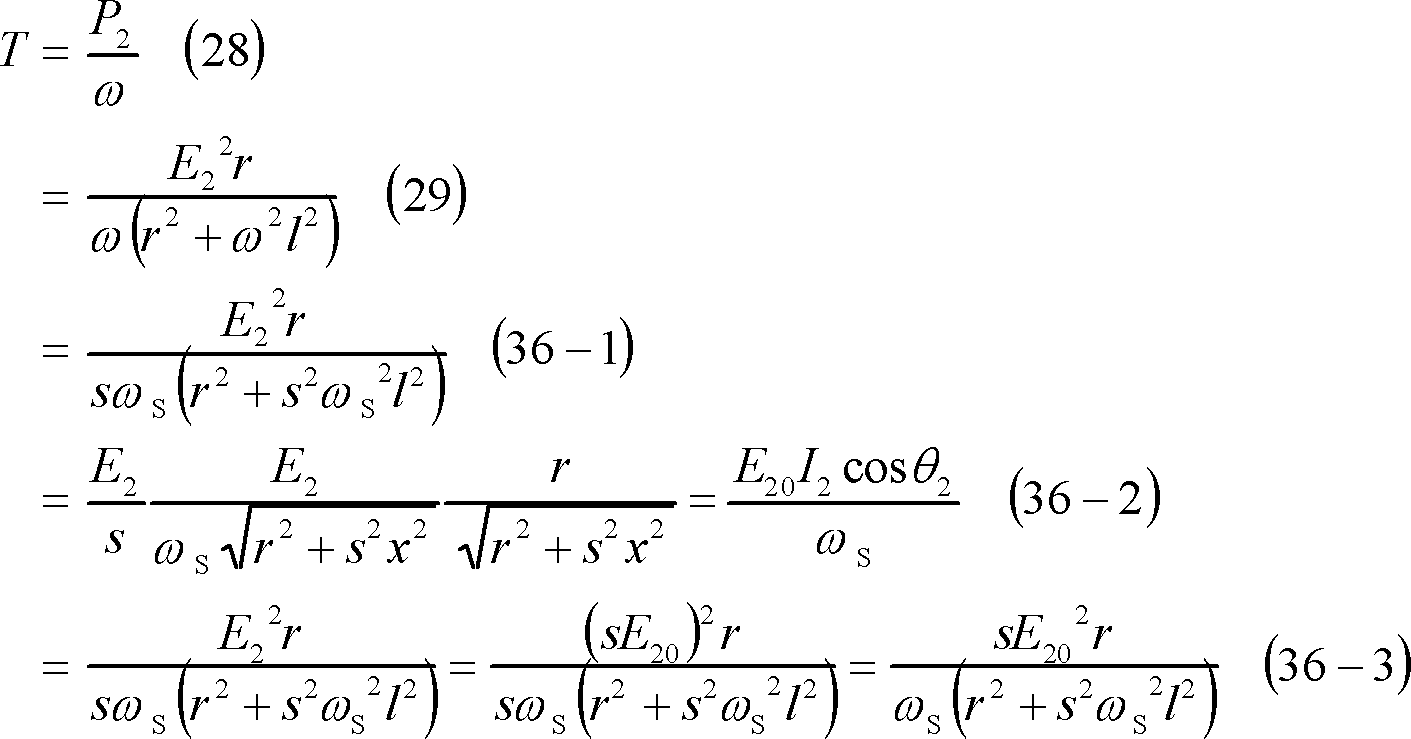
Tとすべりと回転角速度との関係は第6図のグラフとなる。
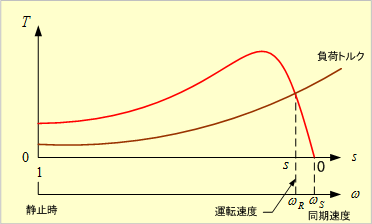
第6図 トルクとすべり・回転数との関係
第7図は回転子におけるエネルギーの流れを示したものである。
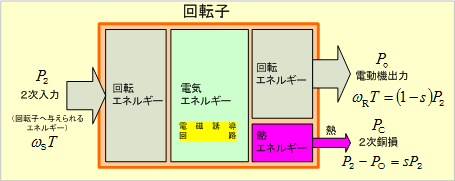
第7図 回転子をめぐるエネルギーの流れ
同図より、電動機出力
![]()
![]() は、
は、
二次入力(回転子へ与えられるエネルギー)
![]()
![]() は、
は、
二次銅損
![]()
![]() は、
は、
以上の関係をまとめると、次式のようになる。
二次銅損の別表現
二次入力の別表現
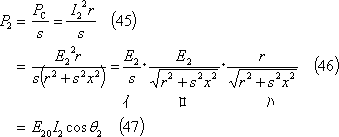
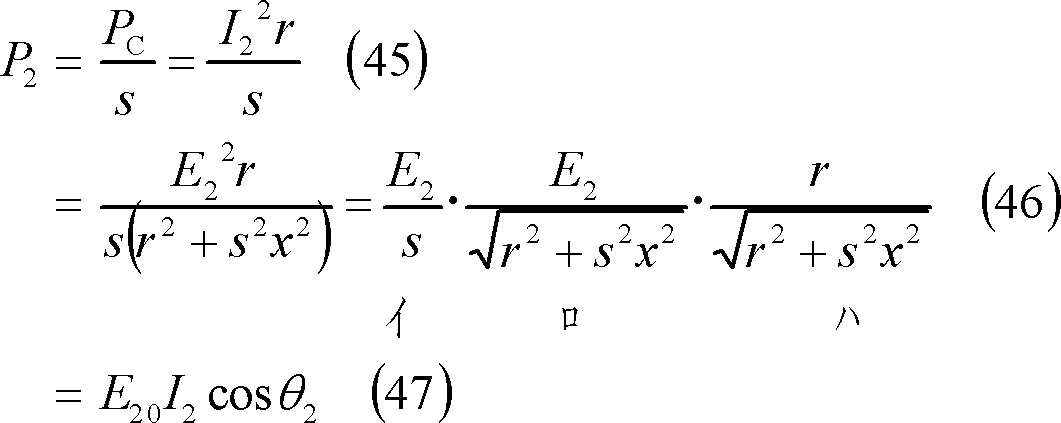
電動機トルクT
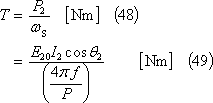
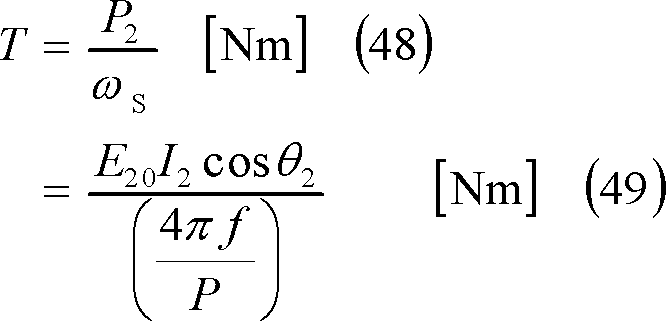
[注]
![]()
![]()
回転子コイルには、巻線形とかご形がある。巻線形は各相に対応した3個の巻線を配置し、スリップリングを介して外部抵抗が接続される。抵抗を加減することで、速度変化、始動トルクの増大、始動電流の抑制等が可能である。
一方、かご形はスリップリングのような接触部がないため、構造が簡単で、堅牢、保守管理が容易なため広く使用されているほぼ定速の電動機である。
これまで扱ってきたコイルは、特性上、コイルの抵抗が小さいほどトルクが大きく、効率がよいので1回巻きのコイルで構成されるが、コイルが1個であると一回転でトルクの山が二つ現れるだけなので回転むらができる。第8図の(a)図に示すコイル配置では4つの山ができる。その他、トルクが小さい、回転子のバランス、などを解決するため、実際には円周に沿って均等に多数のコイルが配置される。コイル導体を流れる電流の経路は図のようにA1、A2、B2、B1、A1の閉路となるが、この内、両端の導体を結ぶ(b)図点線部は回転軸と直角に流れるため回転力に寄与しないので、(c)図橙色線のように円周に沿った経路に変更する。この結果、円周上の導体群の端部を円形導体で接続する「とりかご状」の構造となる。このため、このような回転子構造のものをかご形電動機という。なお、このような接続では導体両端に電位差が生じないため、電流が他の導体に流れトルクの減少等を起こすことはなく、導体部を絶縁する必要もない。
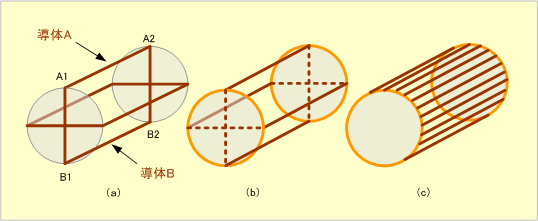
第8図 かご形回転子
第9図①のボタンのように、各相の巻線を円周に沿って2組配置した4極電動機の場合は、各コイルに②のボタンのように対称三相交流電流を流すと、図のような磁束分布となり4極の回転磁界ができる。このため、磁界は③のボタンのように、電流1周期で固定子コイル1組分回転するので、この場合は、2周期で1回転することになる。つまり、毎分の回転数は、60f/2=30fとなる。
したがって、一般にP極電動機の回転磁界の回転速度(同期速度)NSは次式となる。
第9図 4極電動機の回転磁界
電動機の回転方向を変えるには回転磁界の回転方向を変えればよい。具体的には第3図の⑥ボタンに示すように、反時計方向の回転ベクトル3個すべてが同じ方向を向くように電流の位相を調整すればよく、A相電流iAに対して、iBを240°、iCを120°、とそれぞれ遅らせればよい。
(1)コイルがつくるトルク・・・・・・・・・・・第2図、(10)式。
(2)回転磁界の仕組み・・・・・・・・・・・・・交番磁界、回転ベクトル、第3図。
(3)三相交流の回転磁界・・・・・・・・・・・・第3図、(18)式。
(4)三相誘導電動機の構成・・・・・・・・・・・第4図。
(5)回転原理・・・・・・・・・・・・・・・・・第4図、第5図、(29)式、ほか。
(6)すべり・・・・・・・・・・・・・・・・・・(32)式、(33)式。
(7)発生トルク・・・・・・・・・・・・・・・・第4図、第8図、(36)式、(49)式、ほか。
(8)特性・・・・・・・・・・・・・・・・・・・第6図、(43)式、ほか。
(9)三相誘導電動機の構造(かご形回転子)・・・第8図。
問題の解答
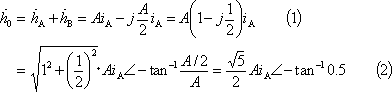
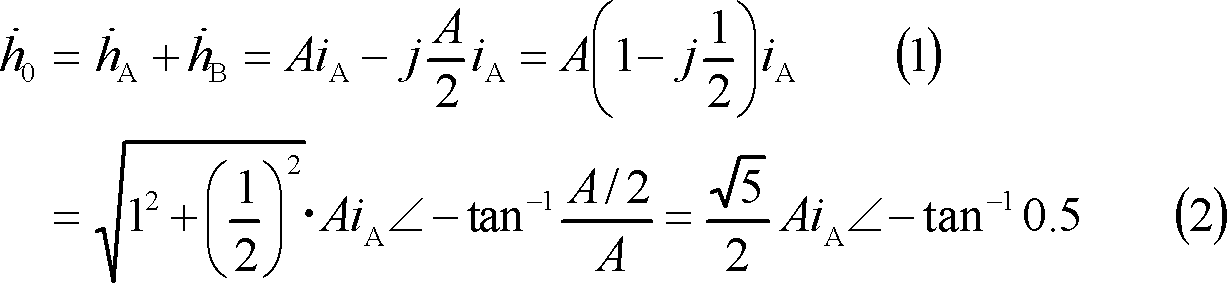
A軸よりB軸方向へ26.6°傾いた方向で、A軸磁界の約1.12倍の大きさ。
