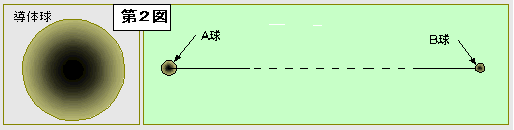
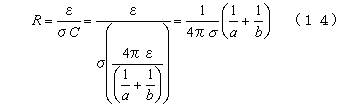① A、B両球とも導体でてきた球である。(第2図の左図)
② 問題の「ただし書き」にあるように、両球の位置関係は球の大きさに比べて十分離れている。しかも、両球をとりまく空間は誘電体あるいは電気抵抗体という物質に満たされている。(第2図の右図)
(1) 《静電容量》 静電容量=電気量/電位差 の関係に注目する。すなわち、両球を電極として、たとえば、A球に+Q
[C]、B球に−Q [C]の電荷をそれぞれ与えて両球間にできる電位差VABを計算すれば、静電容量はC
=Q/VABで求まる。
《電位差の計算》 両球の位置関係が第2図のようであるということは、A球の周囲の電界はB球の電界の影響を受けないということを意味する。また、その逆のこともいえる。
したがって、A球の電位VAは、A球が単独で存在したときの電位に等しく、A球に+Q [C]の電荷を与えた場合の電界を電気力線で表現すると第3図(左図)のようになる。ガウスの定理により導体球から出る電気力線の総数はQ/ε[本]で、球表面から放射状に均等に出てゆく。一方、第3図右図のように、+Q
[C]の点電荷から出る電気力線もQ/ε[本]で、電荷から放射状に均等に出てゆく。このことから、導体球の電気力線分布は、第4図に示すように、点電荷からa
[m]の点より外側と同じ分布であることになる。
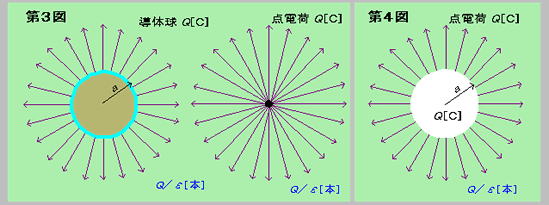
したがって、A球の電位VAは球表面の電位に等しく、第4図で考えれば、点電荷から距離a
[m]の点の電位に等しい。したがって、
![]()
となる。
同様に、B球の電位VBは、
![]()
となる。
この結果、AB間の電位差VABはVAからVBを引けばよく、
![]()
となる。以上のことから求める静電容量C は、
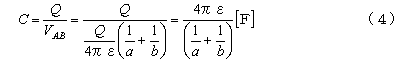
(2)電気抵抗の計算
今度は第2図において、AB両球の周囲が導電率σ の物質で満たされているとして、両球を端子として両端子間の電気抵抗を計算すればよい。
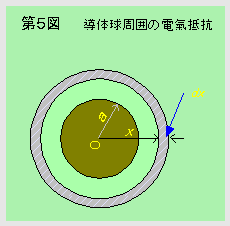
両球が第2図のような位置関係にあることから、たとえば、A球から流れ出る電流は球表面からどの方向にも均等に放射状に流れてゆくので、球の中心からx
[m]のところでdx の長さの部分の抵抗dR は、この部分は第5図の斜線部にあたるので、
![]()
![]()
B球についても電流の流れる方向が逆であることのほかはA球と同じであり、その抵抗RB は、
![]()
となる。
したがって、AB両球間にはRAとRBが直列接続されていると考えられるので、求める電気抵抗RABは、
![]()
となる。
(1) A球に+Q [C]、B球に−Q [C]の電荷を与えたとき各球の周囲にできる電界は、両者の位置関係から他の導体球の影響を受けないとみなせるので、各球の電位は孤立導体球の電位と考えてよく、A球の電位VAは、
となる。同様に、B球の電位VB は、
![]()
となる。AB間の電位差VAB は、VA−VB で求められるから、
![]()
したがって、AB両球間の静電容量C は、
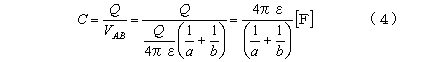
となる。
したがって、A球周辺の抵抗RA は、
同様に、B球周辺の抵抗RB は、
であり、AB両球間にはこれらの抵抗が直列接続されていると考えられるので、その抵抗RAB は、
答 (1)AB両球間の静電容量 C
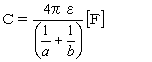
(2)AB両球間の電気抵抗 R

① 導体球のつくる電界は、上記の説明でわかるように点電荷の電界と同様に考えられるのて、電位計算も点電荷の計算に準じて行える。第6図に示す同心導体球の場合について考えてみる。図において、中心部にある半径a
の球を内球と呼び、半径c の球の内部を半径b の球に相当する部分をくりぬいたものを球殻と呼ぶことにする。いま、内球に+Q
[C]の電荷を与えた場合の同心導体球の電位を求めてみよう。
この場合の電界は、内球の中心に点電荷を置いた場合の電界と同じ電界と考えればよいので、同心導体球の電位(内球の電位)V は、ab
間の電位差とc ∞間の電位差(c の電位)を加えればよい。具体的にはV は次式のように、比較的簡単に求めることができる。
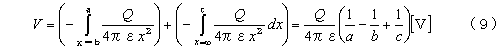
② この問題の電位差の計算は正しく計算できたでしょうか。
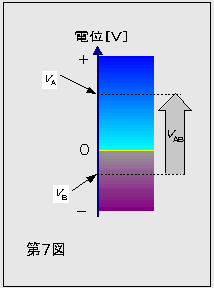
この問題の場合の各球の電位は、VA>0、VB<0なので、両者は第7図のような関係になるので、AB間の電位差VABは(3)式のように計算しないといけない。単純に引き算をする例が多いので注意が必要である。
① 「電極の形状に関係なく、
RC=ε/σ (10)
が成立する。」という関係がある。
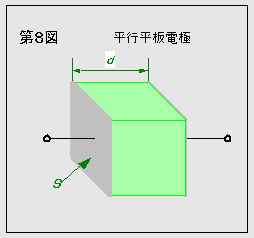
第8図のように、電極面積S の平行平板電極間に、断面積S、長さd
の材料が満たされているとき、(10)式が成立することを確かめてみよう。
この場合の静電容量 C は、 ![]()
電氣抵抗R は、
![]()
![]()
② (10)式の関係を最初から知っておれば、問題(2)の電気抵抗計算は、(10)式の関係を利用して、 次のように求めてもよい。