〜終わり〜
■ぜひアンケートにご協力下さい■


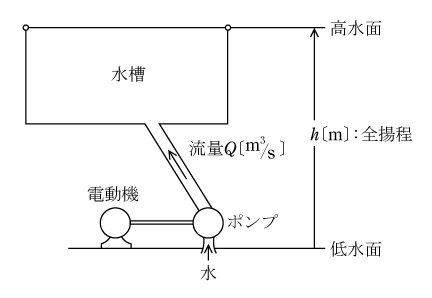
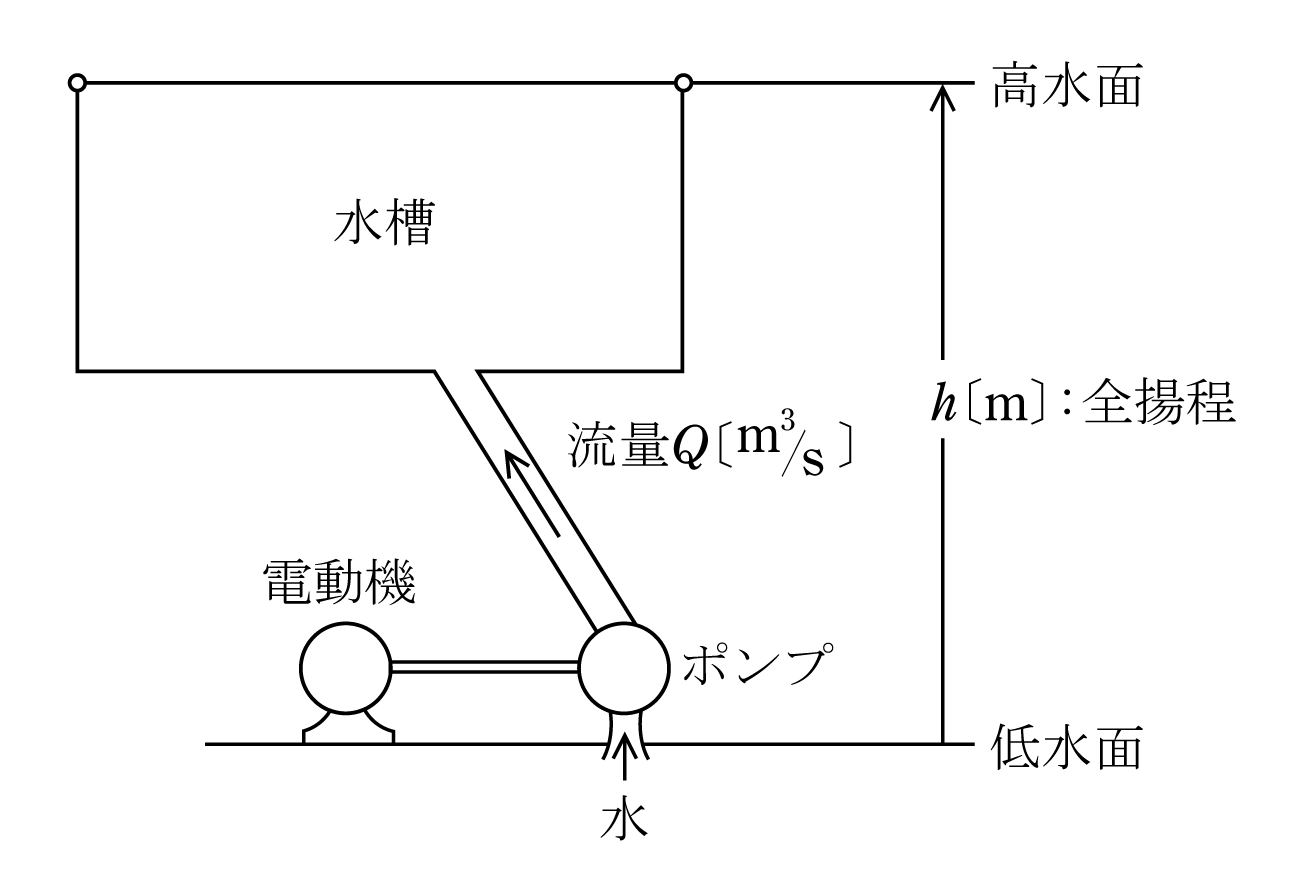
揚水ポンプは第1図のように低所にある水を高所に持ち上げる仕事をする装置である。
持ち上げる高さh〔m〕=低水面から高水面までの垂直距離で全揚程という。水の1秒間の流量Q〔m3/s〕とすると、水の密度は1g/cm3であるから、質量mに換算するとm=Q×1×106〔g/s〕= Q×103〔kg/s〕となる。重力加速度g=9.8m/s2から位置のエネルギーの計算で、1秒間当たりの仕事量W〔J/s〕=〔W〕は( 1 )式となる。
W=mgh=9.8Qh×103〔W〕=9.8Qh〔kW〕 ( 1 )
電動機の出力P〔kW〕は揚水ポンプの効率η1、水が流れる配管内の摩擦抵抗などの損失を総合的に見た効率η2、ポンプの設計に当たり余裕を見込む余裕係数k(一般に1.1〜1.2)から( 2 )式となる。
P=
![]()
![]() 〔kW〕 ( 2 )
〔kW〕 ( 2 )
次に配管の断面積をA〔m2〕、管内の流速をv〔m/s〕とすると、1秒間の流量Q〔m3/s〕=Avとなる。位置のエネルギーと運動のエネルギーの関係はh=v2/2gである。一方、vは電動機の1秒間の回転速度n〔s-1〕に比例するので、nと流量Q、出力P、トルクTの関係は( 3 )、( 4 )式から、出力Pは回転速度nの3乗、トルクTはnの2乗に比例する。
Q=Av∝n h=v2/2g∝n2 P=9.8Qh∝n3 ( 3 )
P=2πnTから T=P/2πn∝n2 ( 4 )
送風機、圧縮機は空気やガスなどの気体に圧力を与える装置で、送風機は気体を送り出す装置、圧縮機は気体を必要な高圧状態にする装置である。今回は送風機に基づいて電動機の出力などについて解説する。
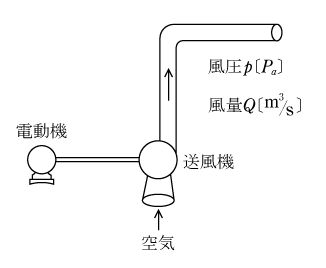
送風機は第2図のように気体に圧力をかけて送り出す装置である。
第2図から風量Q〔m3/s〕、風圧p〔Pa〕とする。pの単位〔Pa〕=〔N/m2〕で、仕事量の単位は〔J〕=〔N・m〕であるから、1秒間当たりの仕事量W〔J/s〕=〔W〕は両者の積で( 5 )式となる。
W=Qp=〔m3/s〕×〔N/m2〕=〔N・m/s〕=〔J/s〕=〔W〕=Qp/103〔kW〕 ( 5 )
電動機の出力P〔kW〕は送風機の総合効率η、余裕係数kから( 6 )式となる。
P=
![]()
![]() 〔kW〕 ( 6 )
〔kW〕 ( 6 )
次に配管の断面積をA〔m2〕、気体の流速をv〔m/s〕とすると、1秒間の流量Q〔m3/s〕=Avとなる。一方、vは電動機の1秒間の回転速度n〔s-1〕に比例するので、nと流量Q、出力P、トルクTの関係は以下のようになる。
Q=Av∝n p∝Qv∝n2 P=Qp/103∝n3
P=2πnTから T=P/2πn∝n2
このように揚水ポンプと同様に出力Pは回転速度nの3乗、トルクTはnの2乗に比例する。
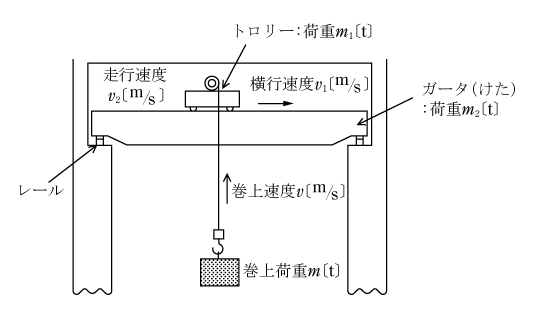
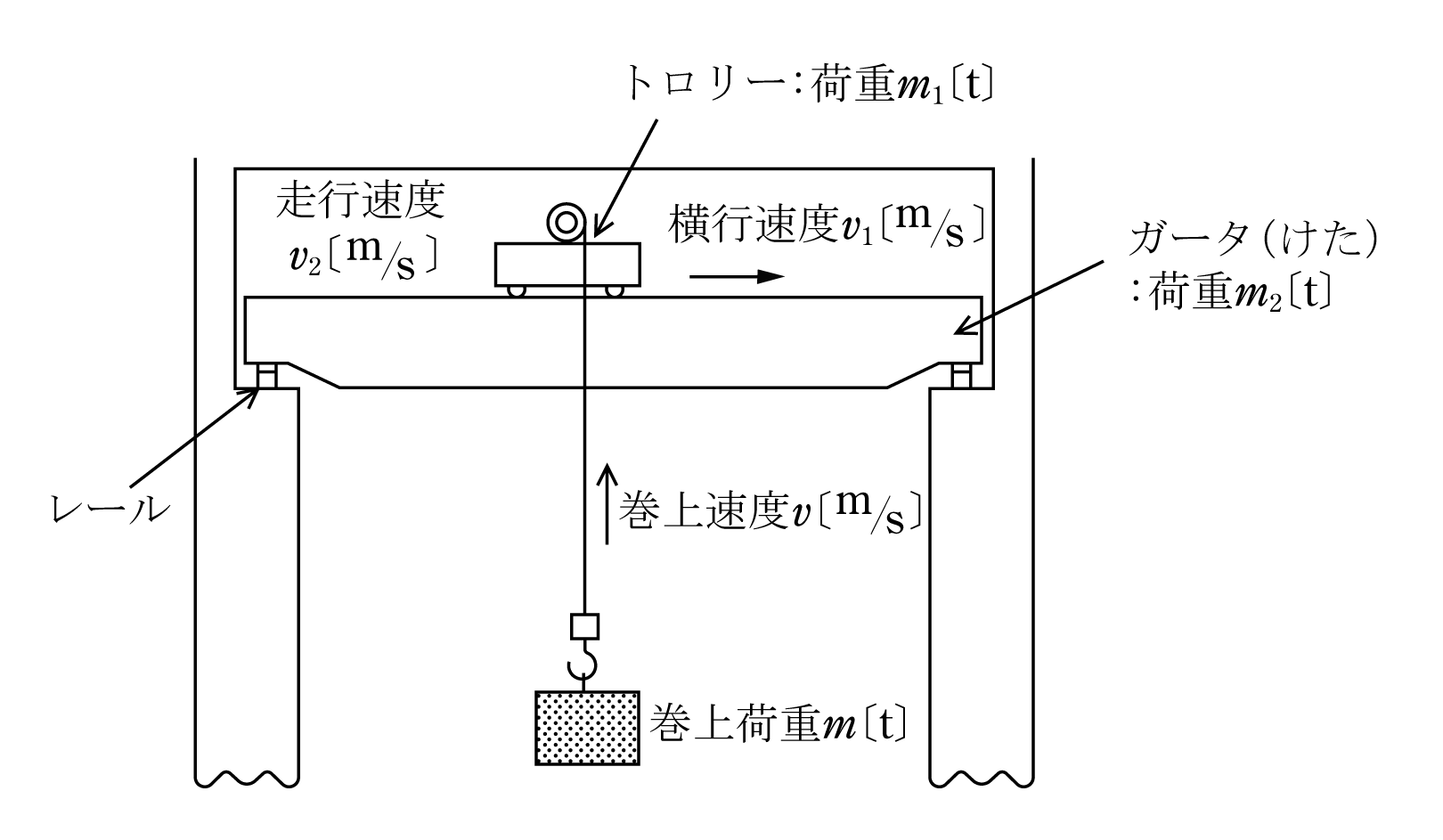
巻上機は物質を上下、左右、直線方向に移動する装置である。このため昇降装置、横行装置、走行装置がある。これらの概念として第3図の分かりやすい天井クレーンをベースに解説する。
( 1 ) 昇降装置
第3図のように荷重を巻き上げる装置である。物体の荷重(巻上荷重)m〔t〕、巻上速度v〔m/s〕、効率ηとすると、電動機の出力P〔kW〕は1秒間に荷重mをv〔m〕高所に移動させるので、位置のエネルギーから( 7 )式となる。
P=
![]()
![]() 〔W〕=
〔W〕=
![]()
![]() 〔kW〕 ( 7 )
〔kW〕 ( 7 )
ここで荷重mの単位を〔t〕でなく〔kN〕を用いると、9.8は不要で( 8 )式となる。試験問題では単位の確認が重要である。
P=
![]()
![]() 〔kW〕 ( 8 )
〔kW〕 ( 8 )
( 2 ) 横行、走行装置
横行、走行するときは水平接触面を垂直荷重が移動するので、水平面と荷重の間に摩擦力が発生し移動に抵抗する。このことから物体の荷重M〔t〕、摩擦の抵抗力を表す摩擦係数(走行抵抗)をμ(小数点)とすると、物体を動かす力F〔N〕=μMgとなる。移動速度が一定でv〔m/s〕、効率ηとすると、電動機の出力P〔kW〕は( 9 )式となる。
P=
![]()
![]() 〔kW〕 ( 9 )
〔kW〕 ( 9 )
ここで物体の荷重Mは第3図から横行、走行の状態で次のように算出する。
( a ) 横行の場合:巻上荷重m+トロリーの荷重m1
( b ) 走行の場合:巻上荷重m+トロリーの荷重m1+ガータの荷重m2
なお、摩擦係数μが〔N/t〕が用いられる場合は( 9 )式の9.8は不要になる。
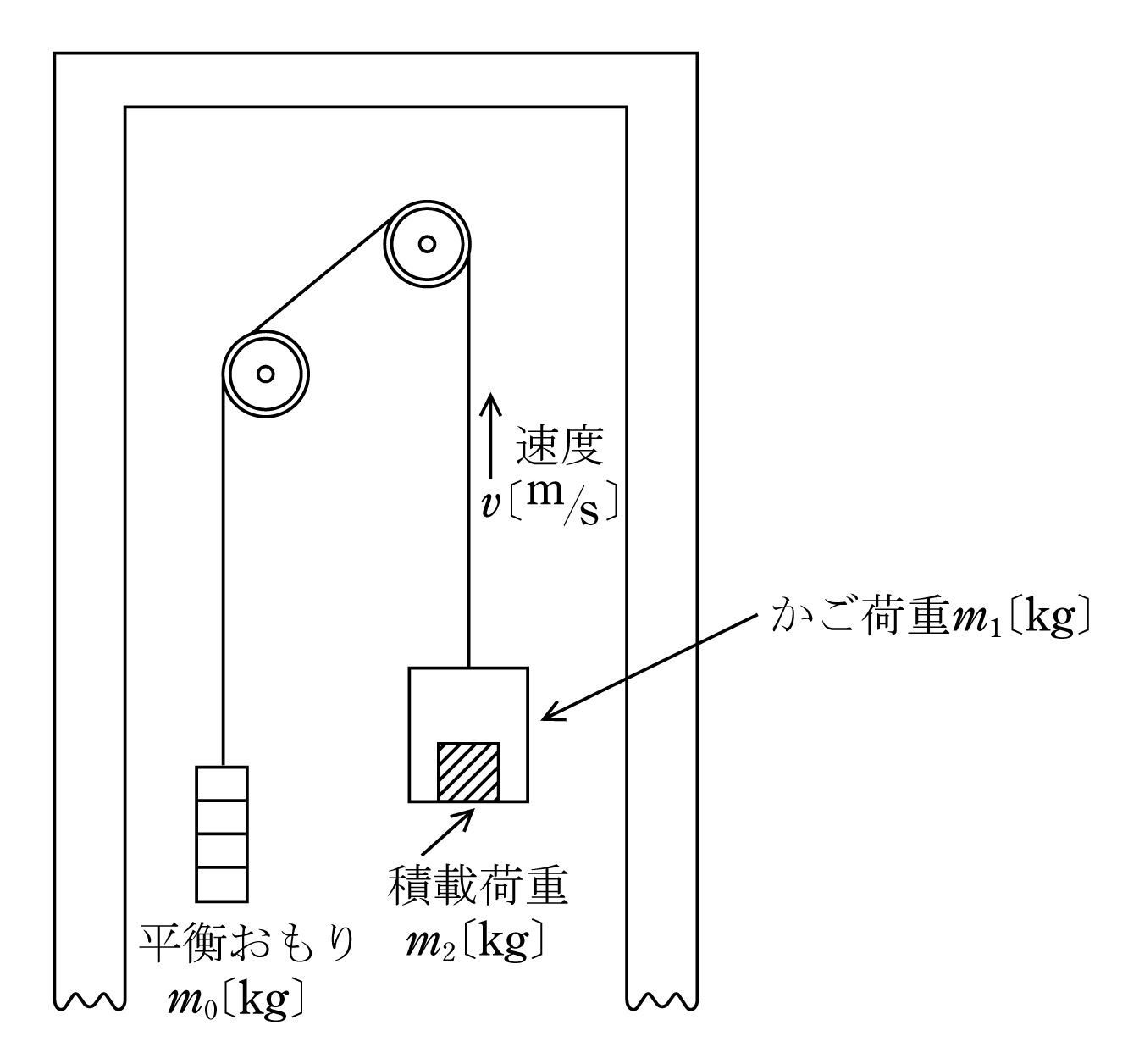
エレベータは巻上機と同様の機能であるが、荷重をできるだけ減少させて効率化を図るため、第4図のように人が乗るかごの反対側に平衡おもりがセットされている。
図からかごの荷重m1、積載荷重m2、平衡おもりの重量m0〔kg〕、上昇速度v〔m/s〕、効率ηとすると、電動機の出力P〔W〕は( 7 )式のmを荷重から平衡おもりを引いたm=m1+m2-m0として( 10 )式となる。
P=
![]()
![]() 〔W〕 ( 10 )
〔W〕 ( 10 )
一般にm0は(m1+m2)の40〜50%に設定されるので、50%とすると(10)式は(11)式になる。
P=
![]()
![]() 〔W〕 ( 11 )
〔W〕 ( 11 )
このように平衡おもりを付けることによって出力Pは半分に減少する。
ここで荷重の単位を〔kg〕でなく〔N〕を用いると、( 8 )式と同様に9.8は不要となる。
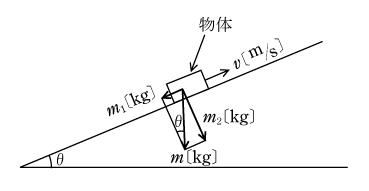
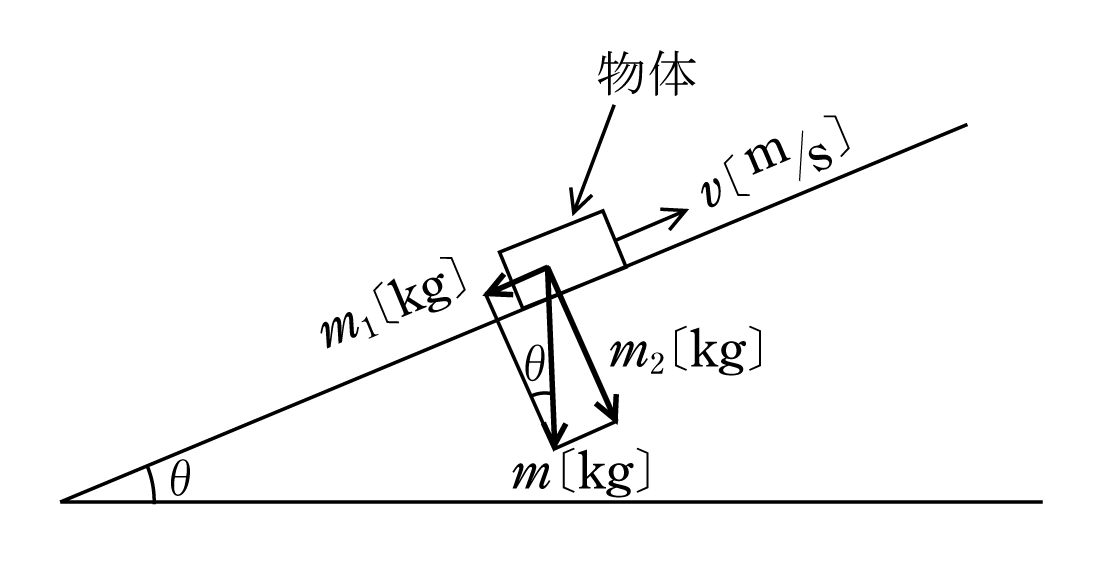
エスカレータは斜面を上下する装置であるから第5図のように傾斜走行する。
図のように水平からθだけ傾斜した面上で荷重m〔kg〕の物体を右方向(下方から上方向)に移動させるには、巻上機の仕事と平面を移動させる走行の仕事が必要になる。
図から物体の荷重mをベクトル図のように斜面方向のm1、垂直方向のm2に分け、斜面に沿った上方向の速度をv〔m/s〕とする。
( a ) 巻上機に相当するの仕事P1
1秒間に垂直方向の移動距離はvsinθから、
P1=mgvsinθ=9.8 vmsinθ=9.8m1v 〔W〕 ( 12 )
( b ) 走行に相当する仕事P2
摩擦係数(走行抵抗)をμ(小数点)とすると、
P2=9.8μm2v=9.8μmvcosθ 〔W〕 ( 13 )
( c ) 合成された電動機の出力P〔W〕
効率η、余裕係数kとする。
P=
![]()
![]()
=
![]()
![]() ( 14 )
( 14 )