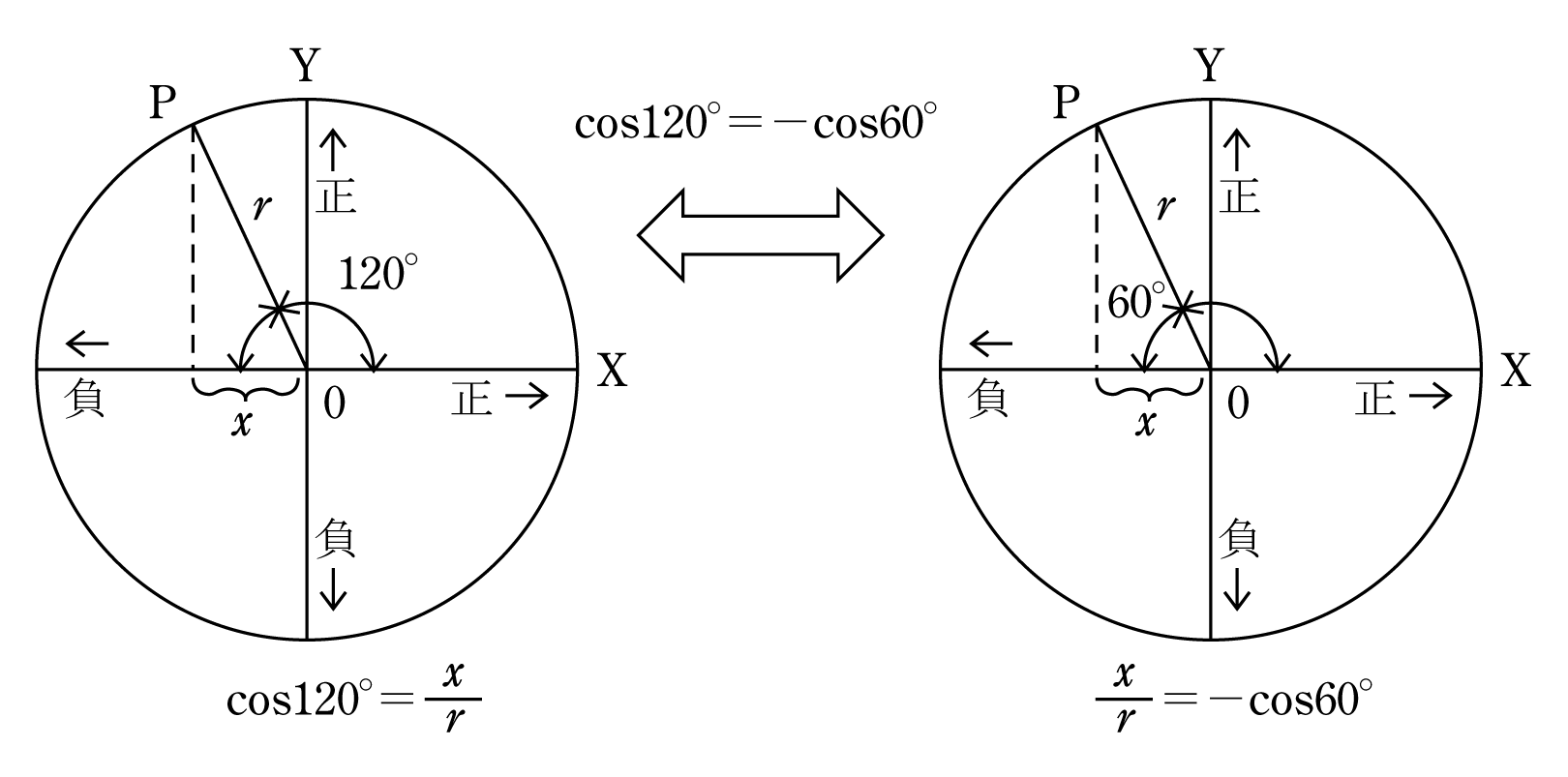〜終わり〜
■ぜひアンケートにご協力下さい■
一般に、交流回路の計算では、瞬時値の代わりにベクトルを用いる。ベクトルは原点を起点とした大きさと偏角を持つ量であって実軸との間に三角形を構成するので、ベクトル計算のカギは三角形の辺の長さや角の大きさの関係を知ることである。三角関数の余弦定理によれば、三角形の二つの辺の長さとそれを挟む角が既知ならば残りの対辺の長さは計算できる。直角三角形を対象とする三平方の定理の一般形であり、ここではなぜそうなるのか、また交流回路計算への応用の仕方について解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
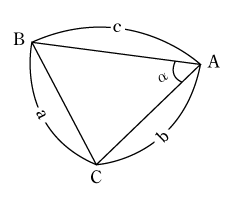
三角形において、第1図のように2辺に挟まれた角がわかっていれば残りの辺は余弦定理によって求めることができる。余弦定理を示すと
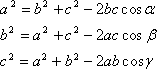
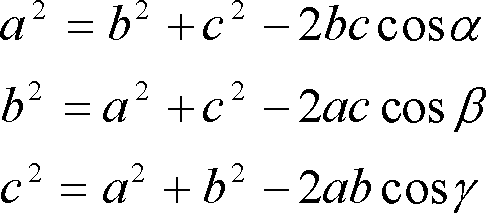
第1式について証明してみると
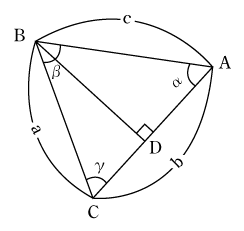
第2図の三角形ABCで、頂点Bから辺ACに垂線をおろし、その足をDとする。
（三平方の定理）
（三平方の定理）
ここで
それぞれ代入すると、
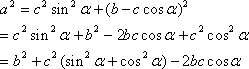
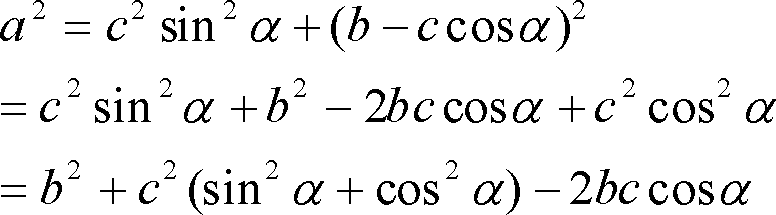
であるから
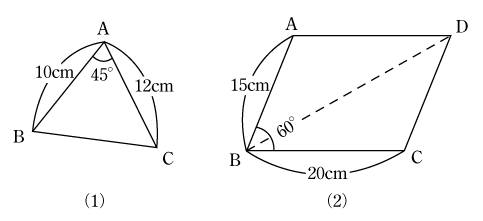
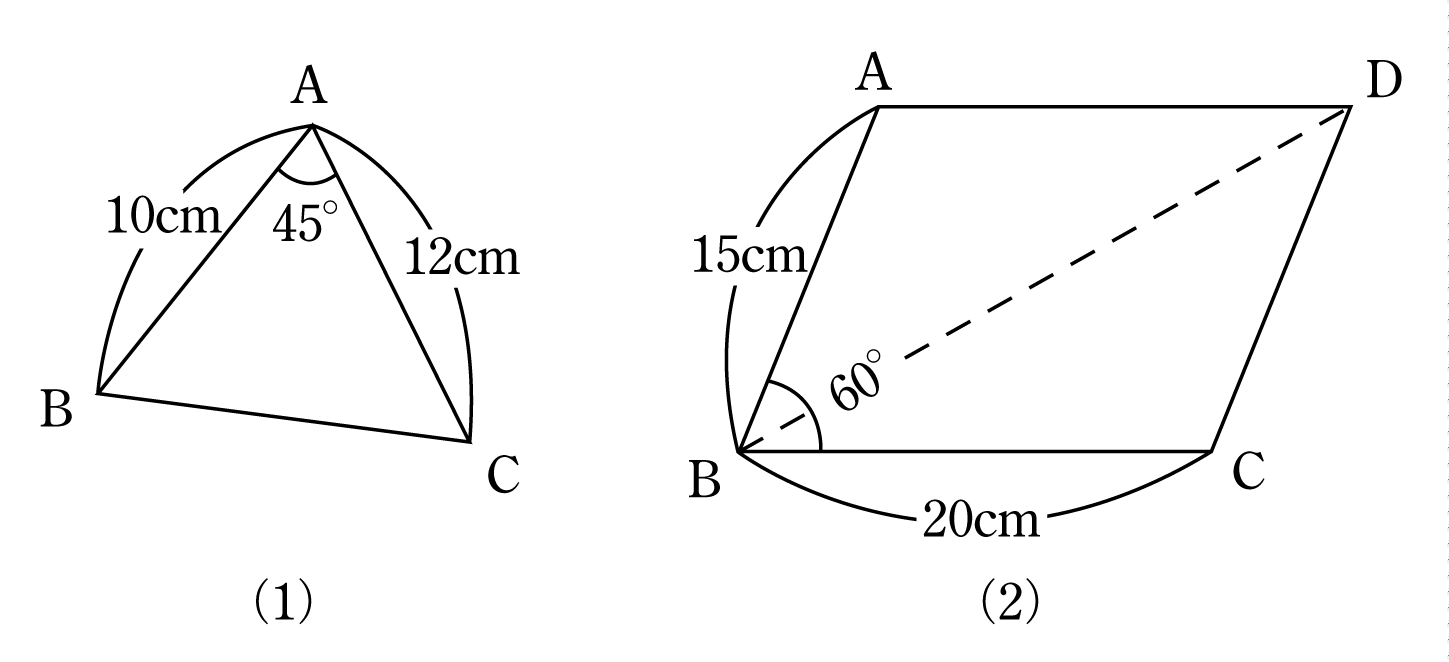
[例題1] 第3図の（1）三角形ABC、（2）平行四辺形ABCDにおける辺BCおよび対角線BDの長さをそれぞれ求めよ。
[解答]（1） 三角形ABCにおいて余弦定理より
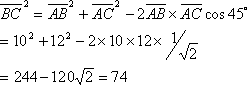
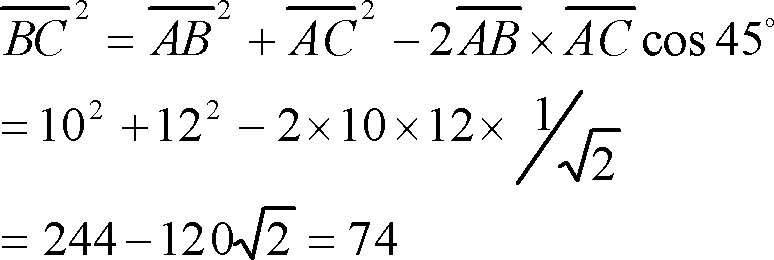
したがって
[cm]
（2） 平行四辺形ABCDにおいて
∠C=180°― 60°=120°
また
[cm]
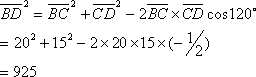
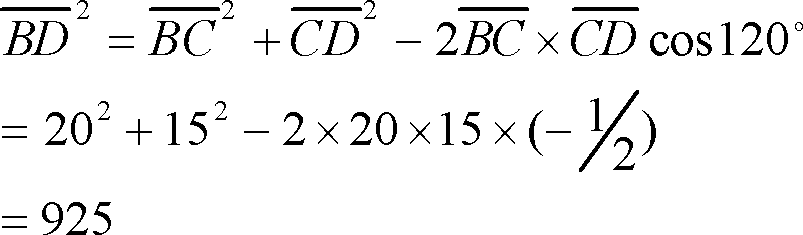
ここで
したがって
[cm]
（注） この計算の中でcos120°=－cos60°として式の値を求めたが、一般に三角比の値を求める場合、鈍角のままでは具合が悪いので、これを鋭角の三角比に変えて求めている。三角関数における三角比の式の簡素化のルールだけはしっかりつかんでおく必要がある。
第4図に、一例としてcos120°=cos（180°－60°）=－cos60°の置き換えについて説明してみた。ほかの三角比についても同じことで、いろいろ応用できるので試みてほしい。
第4図においてcos120°の値とは、半径rの円周上を点Pが左の位置（第2象限）にきたときの
の値のことである。ただし、xは負の値であるから
となる。
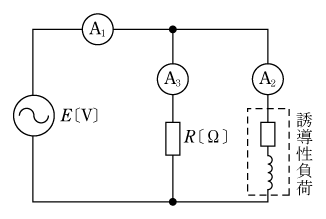
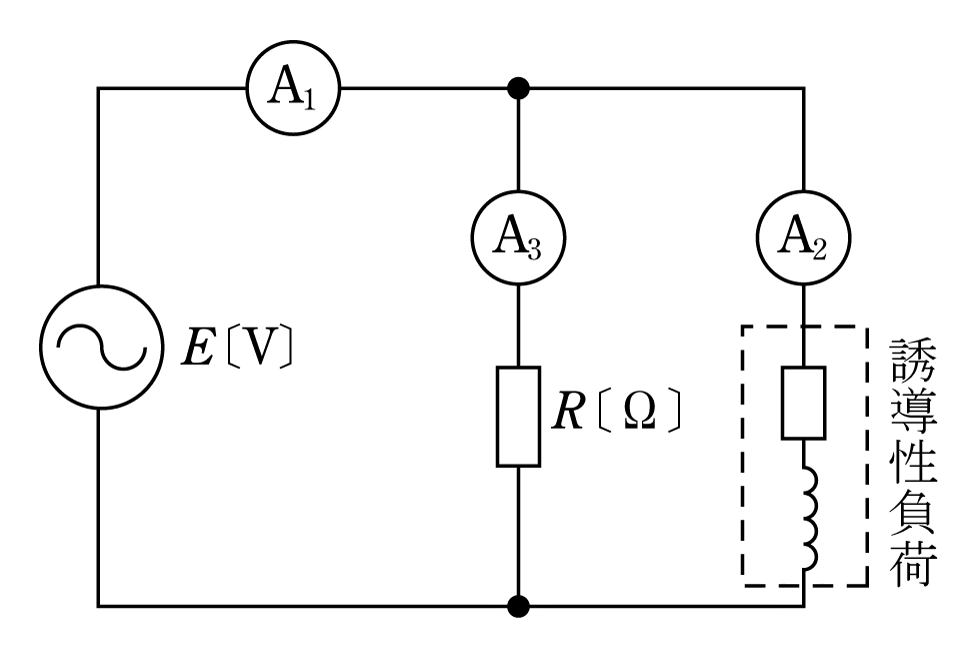
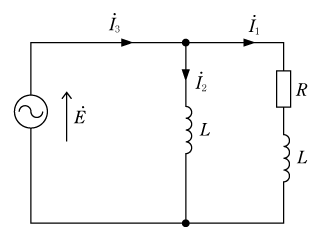
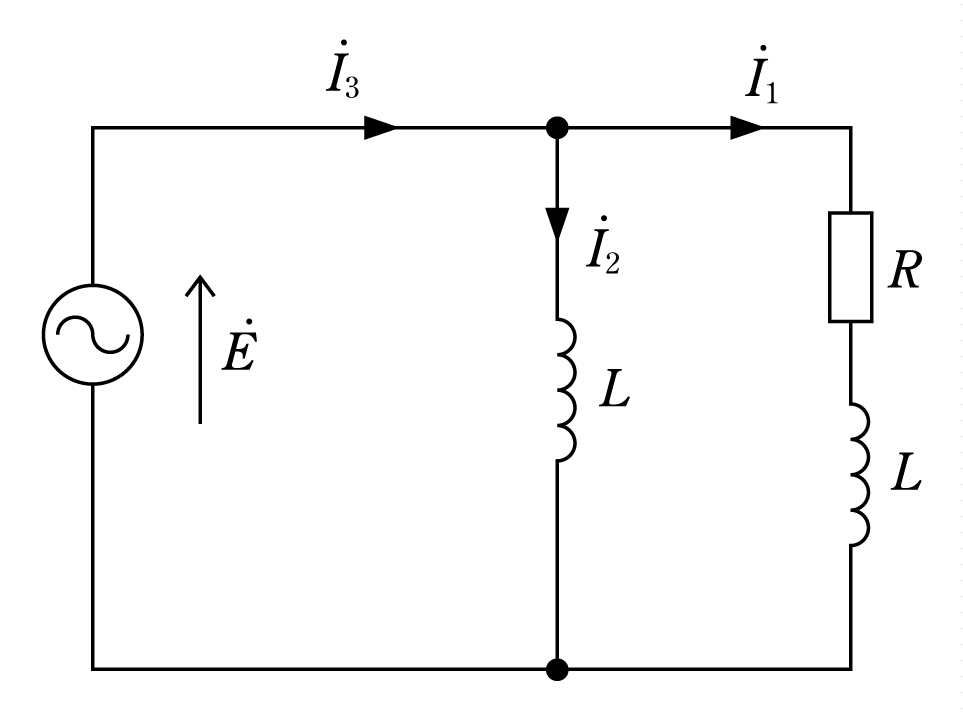
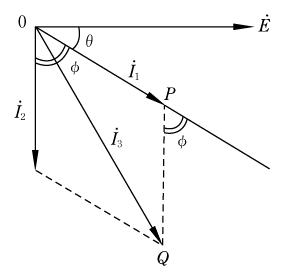
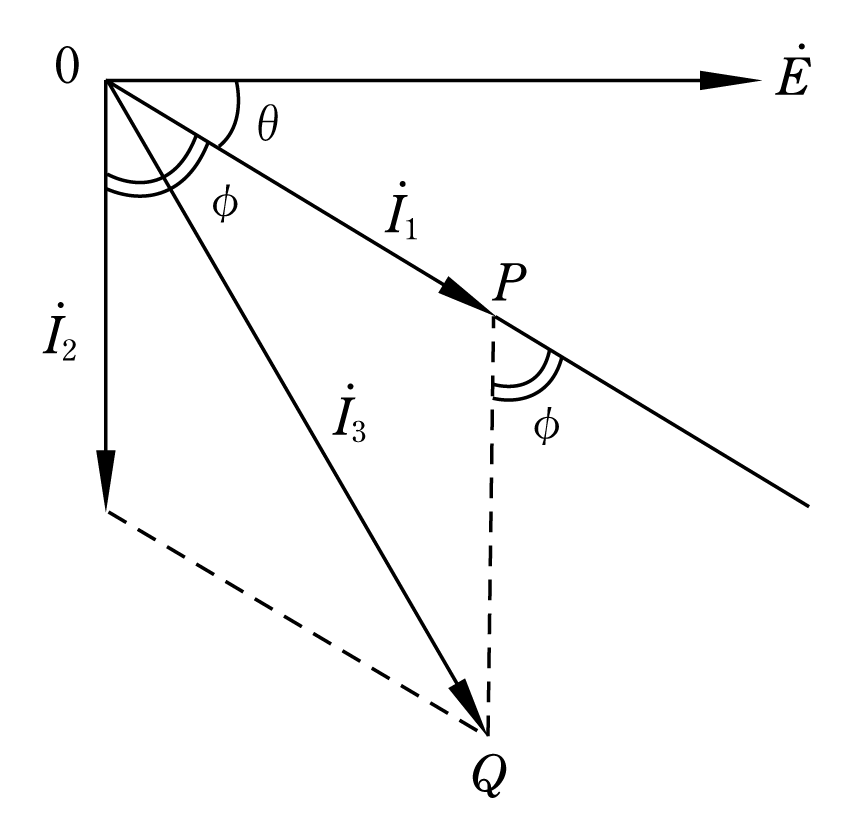
[例題2]力率cosθの誘導性負荷と抵抗Rおよび3台の電流計を接続した第5図のような回路がある。それぞれの電流計の指示をI1、I2、I3とすると力率はいくらになるか。また、負荷電力はいくらになるか。
[解答]
この問題の解答に当たっては、三角関数だけで進めていくというわけにはいかない。この回路のベクトルがきちんと描けないことには三角関数の登場するチャンスがない。余弦定理を交流回路で使うためには、まずベクトル図を正しく書くことを念頭においてほしい。
[解きかたの順序]
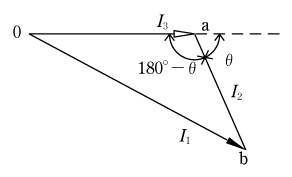
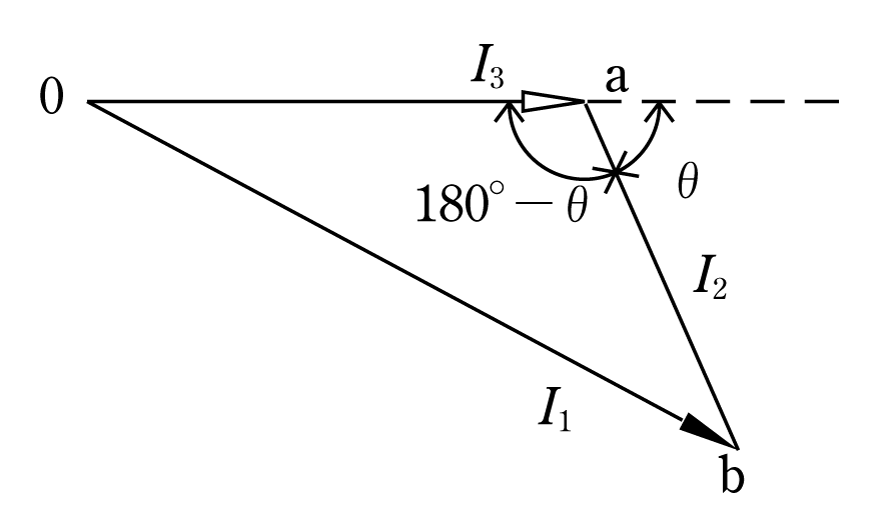
①第6図のようにベクトル図を描く
②余弦定理をどこに当てはめるかを考える
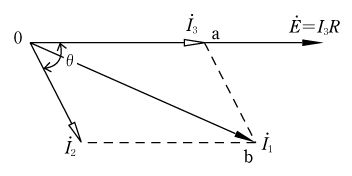
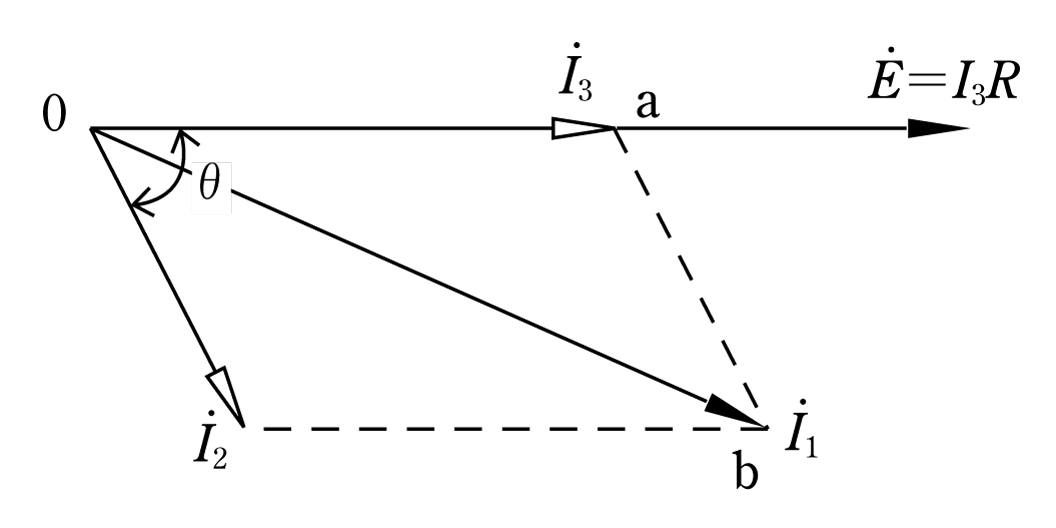
（△oabに適用する）
2辺と挟まれる角をどこにおいたらよいかが余弦定理を使う場合の問題点であるが、この場合I1、I2、I3で囲まれている △oabに着眼してほしい。角度は180°―θを使うことに注意し、三角比の簡素化を図ると式がまとまりやすくなる。（第7図）
③ cosθを求める
④ 負荷電力Pを求める。cosθを求めれば電力Pは求めることができる。
第7図のベクトル図の△oabに余弦定理をあてはめると
ここで、
だから
したがって
となる
さらに電力（負荷）Pは
さらにcosθを代入すると
結局、抵抗Rの値と3個の電流計の値だけで負荷電力を知ることができる。
[例題3]第8図の回路に、交流電圧200Vが加えられているとき、各部の電流I1、I2、I3はそれぞれ18A、20A、34Aであったという。負荷の消費電力、無効電力、および力率を求めよ。
[解答]
ベクトル図を描くと、第9図のようになる。
△OPQに着目して余弦定理を適用すると
これから
ベクトル図より
であるから
である。
したがって
力率は0.8であるから消費電力Pは
無効電力Qは
var
var
