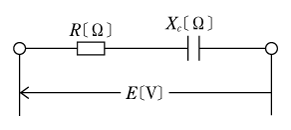〜終わり〜
■ぜひアンケートにご協力下さい■
交流回路の計算では、オームの法則をインピーダンスを用いて表す方法と、その逆数であるアドミタンスを用いて表す方法がある。大ざっぱに言えば、R, L, Cの直列回路はインピーダンス、並列回路はアドミタンスで定式化したほうが式が簡単になるが、これが決まりというわけではなく、ケースに応じて使い分けるほうがよい。ここでは、 具体事例を用い、解法選択の違いにより、問題が難しくなったり、簡単になったりすることを学習する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
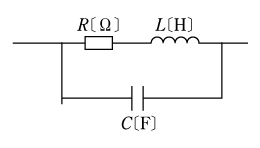
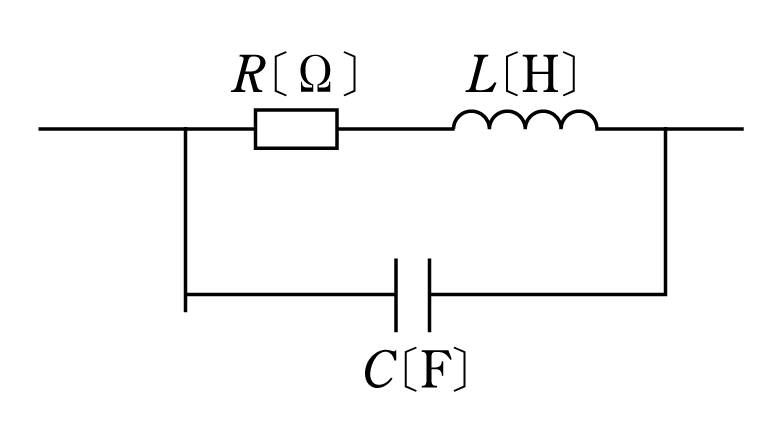
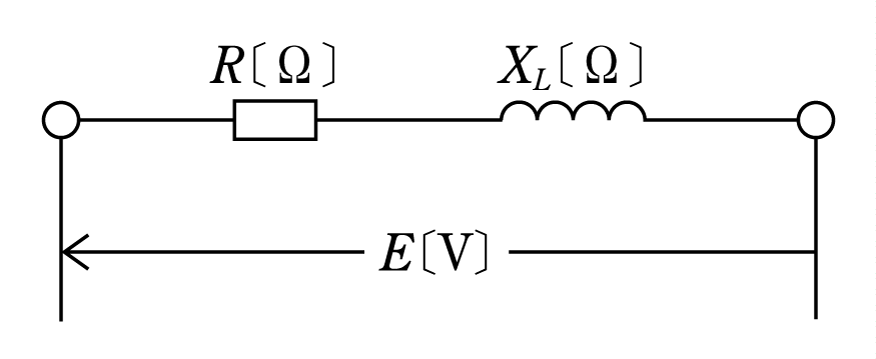
[例題1]第1図の回路におけるインピーダンス
を求めよ。
[解答例①]インピーダンスを直接求める
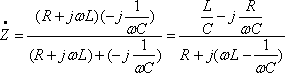
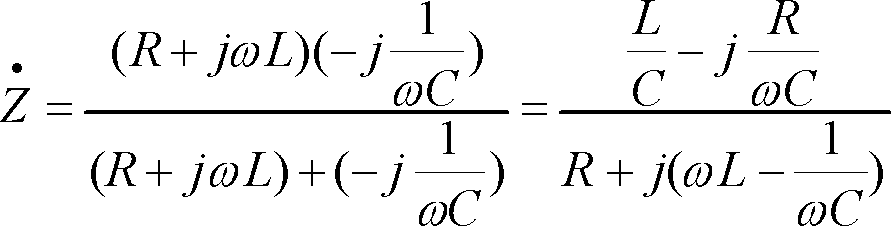
この式は途中であるが、分母、分子共に分数を含んでいて、あとの計算に相当労力を使うことになるので、つぎのように処理したほうが良い。
[解答例②]インピーダンスを直接求める
の変換を使うと、
よりずっとやさしくなる。
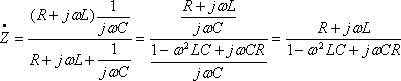
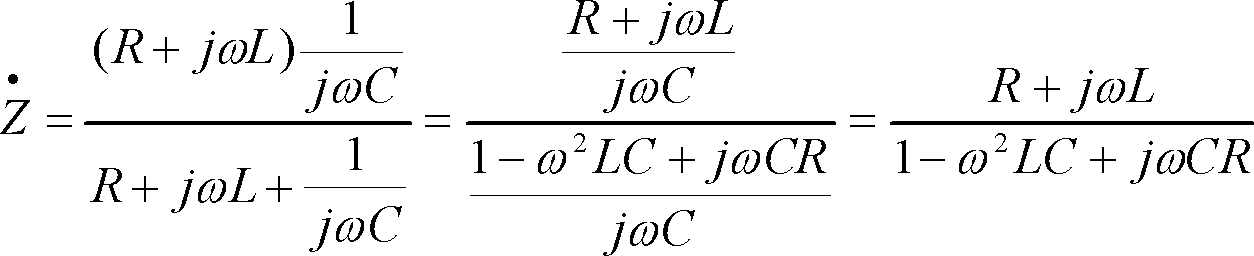
[解答例③]アドミタンスからインピーダンスを求める
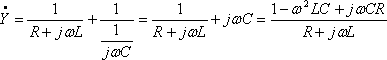
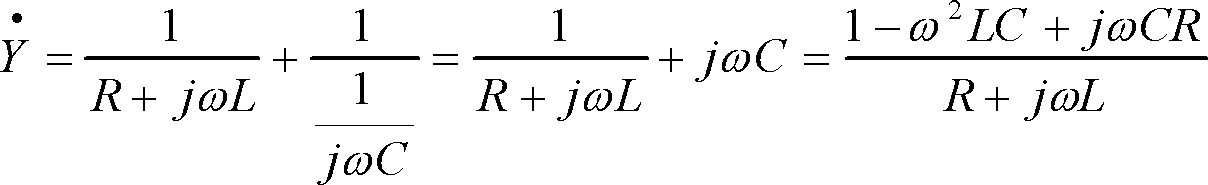
したがって
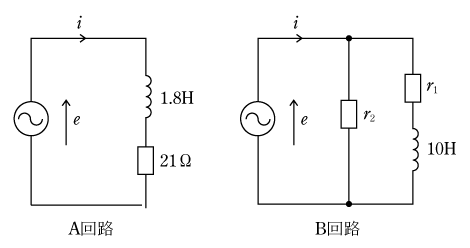
題意より角周波数ω=2πfであるから、R,L直列回路のインピーダンスは
であるから
したがって回路Aのアドミタンスは
また、回路Bのアドミタンスは
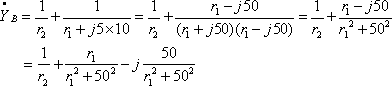
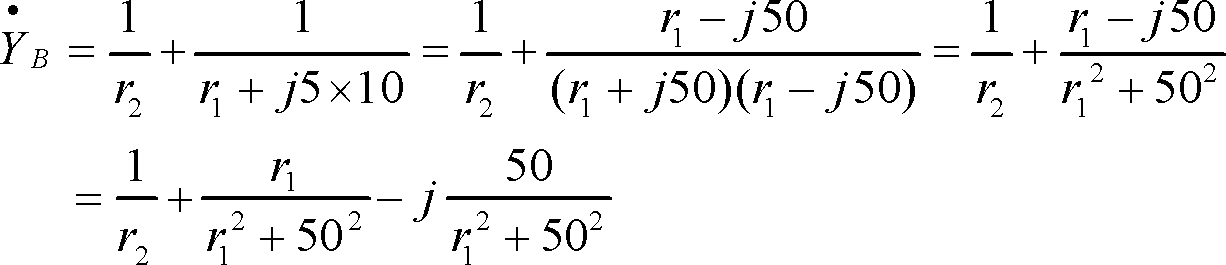
題意より
であるから、この二式の実数部どうし、虚数部どうしは等しいことになる。 したがって
（1）
（1）
（2）
（2）
（2）式の逆数をとると
したがって
これを（1）式に代入して
したがって
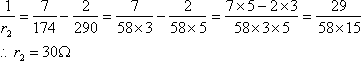
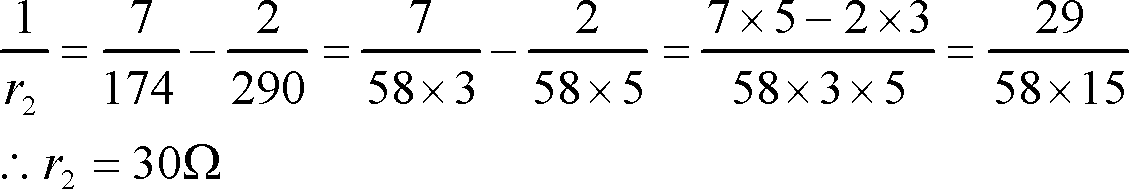
ここで、アドミタンスをコンダクタンスとサセプタンスにわけた場合の問題解法にどんな利点が生じるかについて調べてみる。
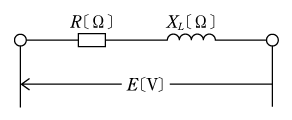
いま、第3図のような誘導性回路について、アドミタンスを求めてみると
この実数部をg、虚数部をbと置くと
となる。このとき、gをコンダクタンス、bをサセプタンスと呼ぶ。
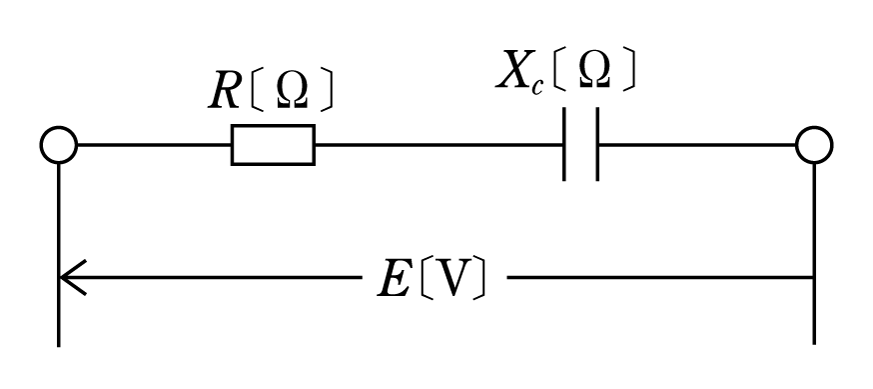
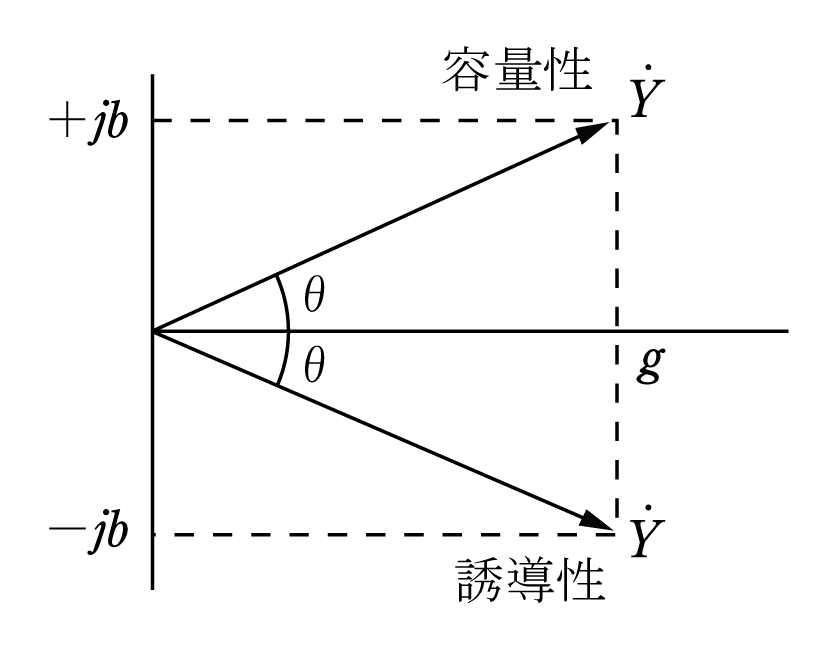
また、第4図のような容量性回路の場合には、
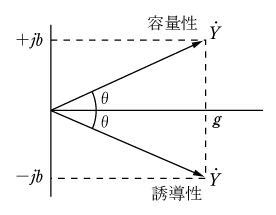
となる。つまり、誘導性回路ではサセプタンスは負となり、容量性回路では正となることがわかる。いま、これらをベクトルであらわしてみると、第5図のように
、
また
、
であることもわかる。
以上の内容をふまえて、つぎの問題に応用してみよう
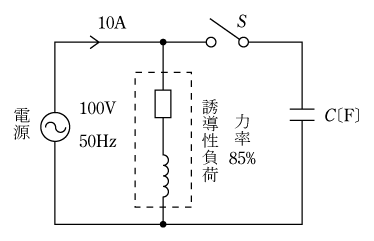
[例題3]第6図のように、50Hz、100Vの電源に単相誘導負荷を接続したとき流れる電流は10Aで、力率は85％であった。この負荷にコンデンサCを接続して、力率を100％にしたい。コンデンサの静電容量をいくらにすればよいか。
[解答の方針]
この誘導負荷を見て、抵抗をR、誘導負荷をωLなどとおくことは考えなくてもよい。誘導負荷のアドミタンスが
で表わされることを利用して解くことができる。
[解答]題意により
であることがわかる。
また力率が85％であることからcosθ=0.85 したがって
これにより、誘導負荷のアドミタンスは
となる
したがってコンデンサを並列に接続した場合の合成アドミタンスは
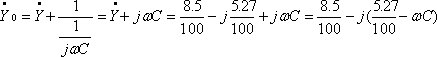
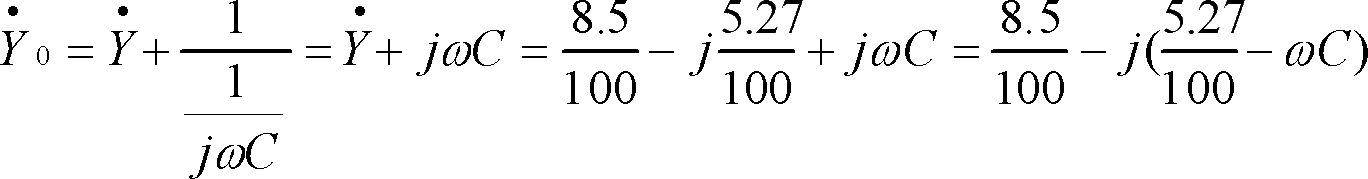
力率が100％になるためには、虚数部
が0になればよい。
より
π=3.14 f=50を代入して
Cの値は、ほぼ0.17×10－3[F]=170[μF]となることがわかる。
[別解]
この問題をアドミタンスを使わないで、別の立場から解いてみるとどうなるだろう。
力率85％の誘導負荷を流れる電流をIとすると、このIは有効電流と無効電流のベクトル和であることがわかる。つまり、遅れ電流があることになる。どれだけの遅れ電流かというと、つまり無効分の大きさは
となる
ところが、コンデンサは進み電流を流すから、この5Aに相当する分だけコンデンサに電流を流させれば、お互い打ち消しあって無効分は0になってしまうわけである。そこでコンデンサに流す電流Ic=5として、静電容量Cを求めればよいことになる。
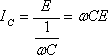
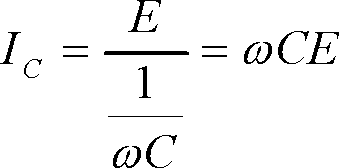つまり
この関係を満たすCは
すなわち 170μFの値の容量をもつコンデンサを設置すればよいことになり、結論は一致する。
