〜終わり〜
■ぜひアンケートにご協力下さい■
オペアンプを使った発振回路、微分回路及び積分回路の演算原理について解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
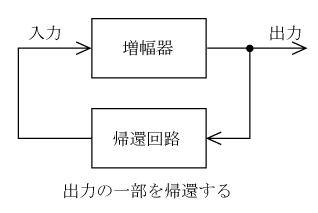
発振回路は第１図に示すように増幅器と帰還回路から構成されている。増幅器が広帯域の周波数を増幅するものである場合、その出力からは増幅された広帯域の信号が出力される。帰還回路は出力信号の中に含まれる信号のうち、発振を持続させたい周波数を選択し、これを増幅器の入力として正帰還させるものである。正帰還された信号は増幅回路で増幅されるが、増幅回路の非直線性や増幅回路の飽和特性によって、やがて一定振幅に落ち着く。これが発振回路の原理である。
なお、発振を継続させるにはそのきっかけとなる入力信号が必要である。この信号は、発振回路に電圧を印加したときに生ずるノイズや減衰振動などである。
ただし発振回路が発振するきっかけとなる減衰振動は時間の経過とともに消滅してしまうため、発振を継続するには、次式の条件を満たす必要がある。
（1）
（1）
ここに、Vβ：帰還電圧、VI：入力電圧
いま、増幅回路の増幅度をA、帰還回路の帰還率をβとすると、（1）式から、
（2）
（2）
とならなければならない。一般にA、βにはリアクタンス分が含まれるので複素数になる。すなわち、増幅度を
、帰還回路の帰還率を
とすると、
（3）
（3）
（4）
（4）
の二つの式が成立する必要がある。（3）式を発振回路の振幅条件、（4）式を周波数条件という。
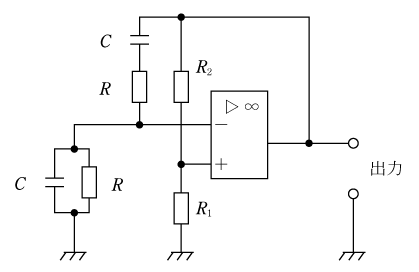
増幅回路にオペアンプを用いれば発振回路を構成することができる。第２図はウィーンブリッジ発振回路である。この図における振幅条件及び周波数条件（発振周波数）はそれぞれ次式で示される。
振幅条件 ：
（5）
周波数条件：
（6）
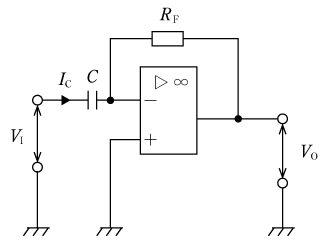
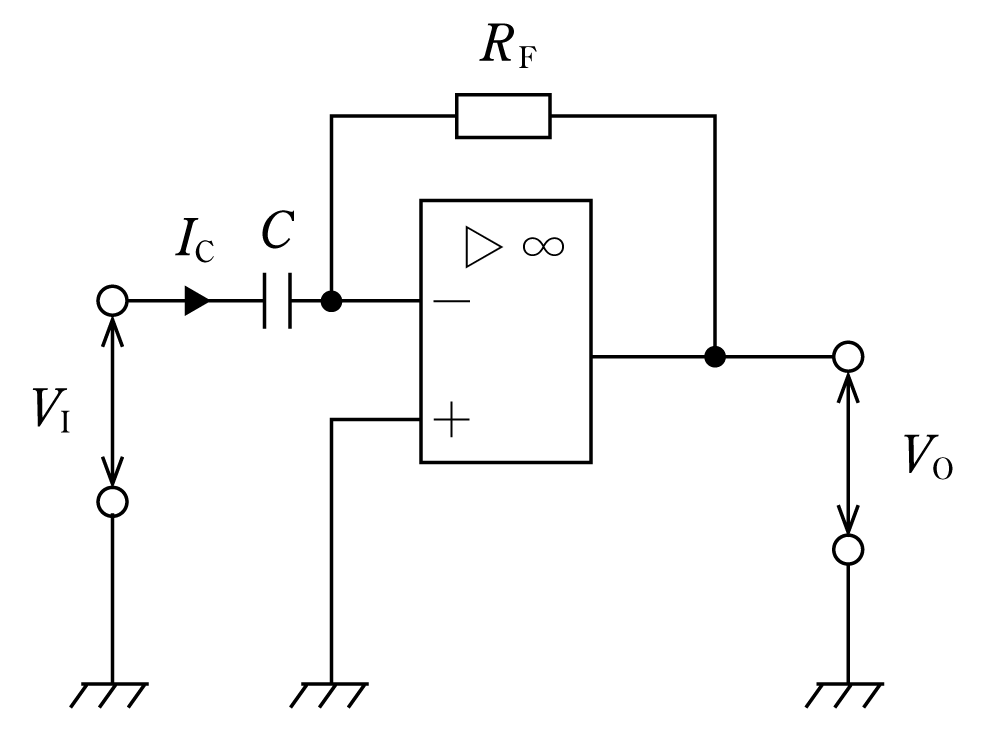
第３図は入力された信号を微分した信号に変換して出力する微分回路である。微分回路は反転増幅回路の入力抵抗をコンデンサに置き換えたものである。非反転入力端子が接地されているので、反転入力端子は仮想短絡（イマジナルショート）によって接地されたことと等価である。したがって、入力電圧をVIとすれば、コンデンサCを流れる電流ICは、
（7）
（7）
となる。非反転入力端子の入力インピーダンスが無限大であるから、この電流はすべて帰還抵抗RFに流れる。よって、出力電圧VOは、
（8）
（8）
と求まる。したがって、第３図の回路は入力電圧の時間微分に比例した出力が得られることが分かる。
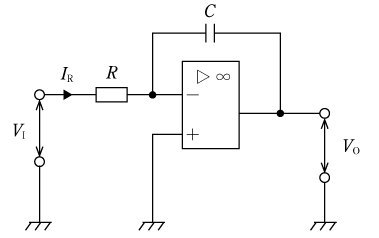
第４図は入力された信号を積分した信号に変換して出力する積分回路である。積分回路も微分回路と同様に反転増幅回路を変形したもので、帰還抵抗RFに代えてコンデンサCを接続したものである。非反転入力端子が接地されているのでイマジナルショートによって反転入力端子も接地されたことになる。よって、抵抗Rに流れる電流IRは、
（9）
（9）
となる。この電流はすべてコンデンサCを流れるので、出力電圧VOは、
（10）
（10）
と求まる。したがって、第４図の回路は入力電圧の時間積分に比例した出力が得られることが分かる。