機器の銘板には、機器の製作や取扱い運用に必要な種々の項目が記載されている。変圧器の場合、JIS、JECにより記載事項が定められている。ここでは油入及びモールド変圧器の銘板に記載された主な事項について、等価回路を基にした式を用いて特性を解説するなどその意味を通じて変圧器への理解を深めることとする。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
※テキスト中の図はクリックすると大きく表示されます
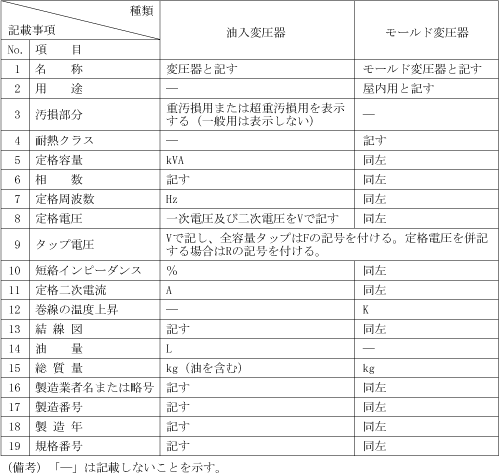
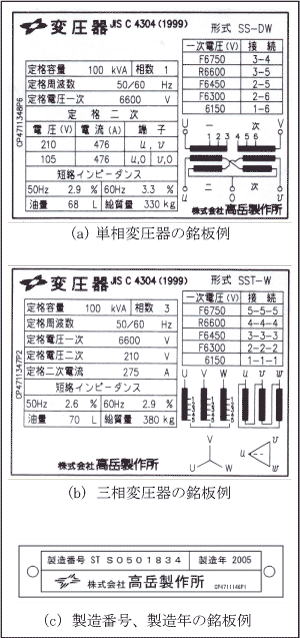
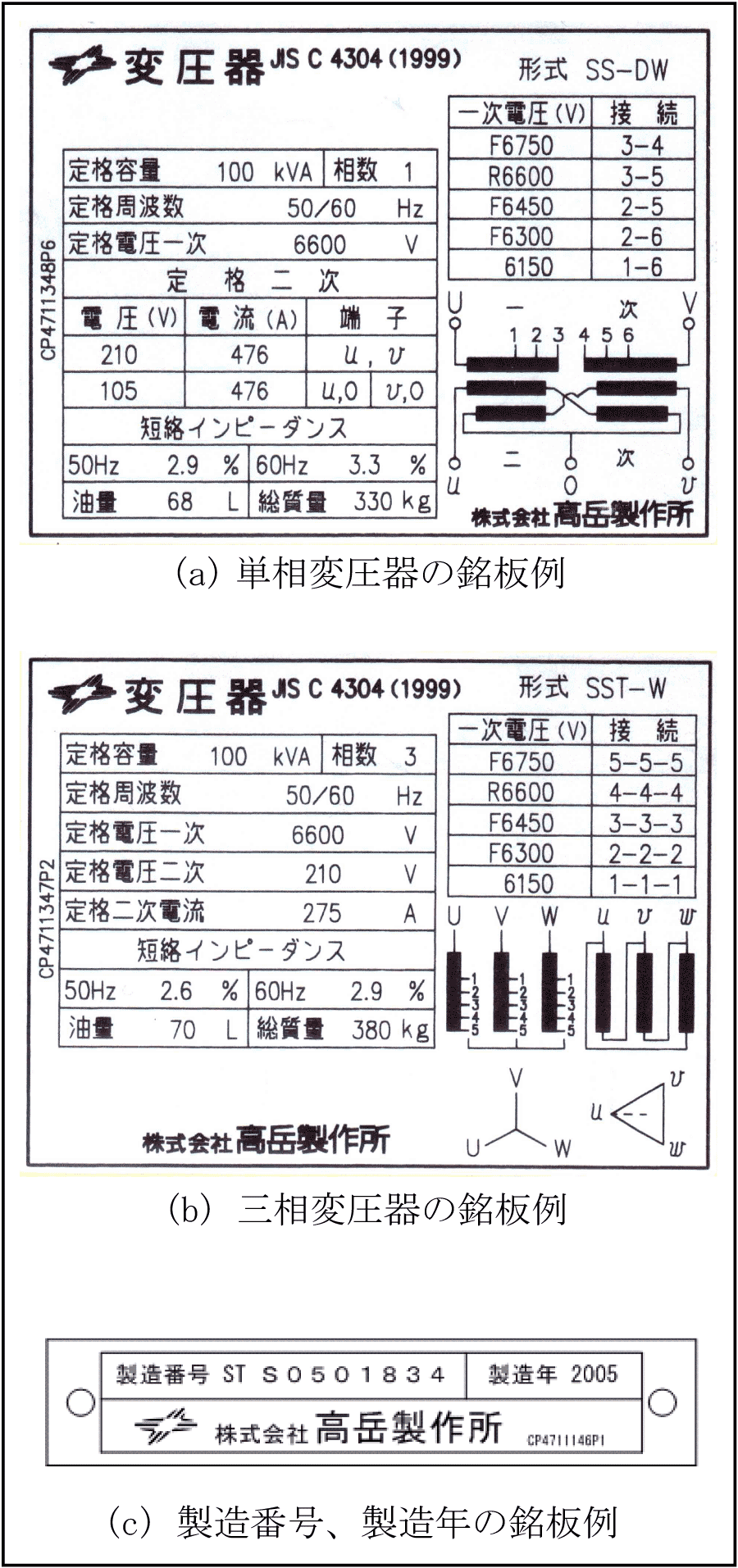
JIS、JECでは、「変圧器には見やすい箇所に銘板を取り付けなければならない。」と規定されている。第1表は配電用6kV変圧器の銘板記載事項であり、第1図に油入変圧器の銘板例を示す。
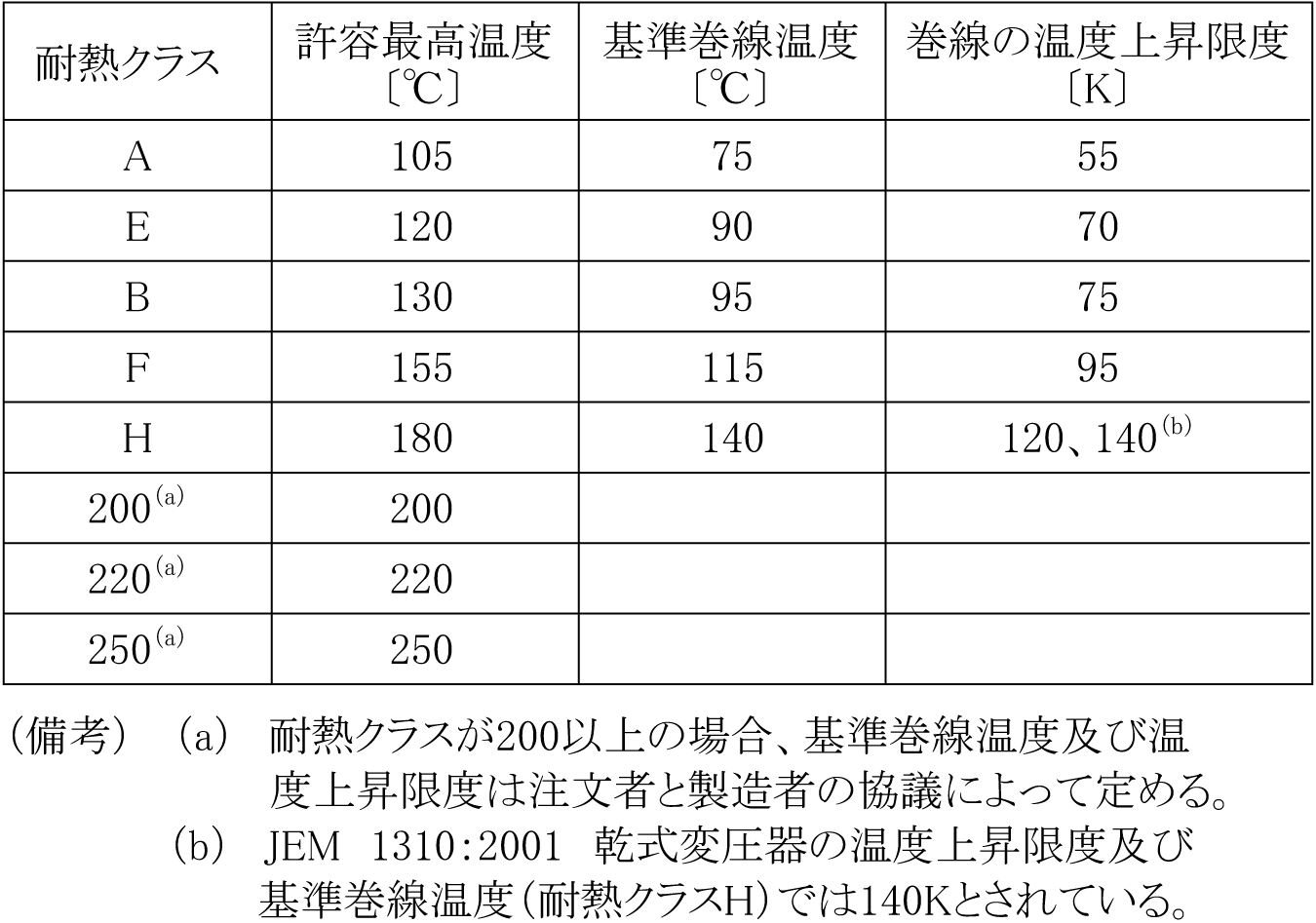
(1) 耐熱クラス
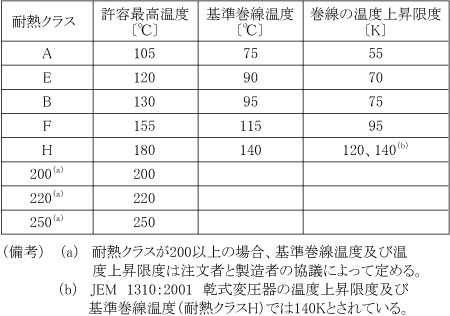
変圧器は使用される絶縁材料の耐熱特性によって第2表に示す耐熱クラスに分類される。絶縁材料には、絶縁油、SF6ガスのほか、クラフト紙、プレスボード、マイカ、ガラス繊維、エポキシ樹脂、シリコーン樹脂、アルキッド樹脂など種々の材料が使用され、それぞれ許容最高温度が定められている。これらの各種絶縁材料を使用することにより、油入変圧器の耐熱クラスはA、モールド変圧器はB、F、及びHが適用されている。変圧器は標準使用状態で使用するとき、巻線の温度上昇限度(巻線の温度と周囲温度との差の限度)を超えず、絶縁物の各部が耐熱クラスの許容最高温度を超えないように設計されているが、周囲温度が最高値(40℃)を超えているとき、あるいは過度の過負荷運転などによって許容最高温度を超えるおそれがある。変圧器の寿命は最高点温度によって最も大きな影響を受けるため、許容最高温度を超えた長時間の持続運転は、変圧器の期待寿命とされる30年を短縮することにつながる。なお、標準使用状態とは次の状態をいう。
- 標高 1,000m以下の場所で使用する。
- 周囲温度 屋内用 −5℃〜+40℃、屋外用 −20℃〜+40℃、なお、日間平均気温が35℃を超えず、かつ年間平均気温が20℃を超えないようにする。
- 回路の電圧波形 変圧器が接続される回路の電圧波形はほぼ正弦波とする。
- 三相回路の電圧平衡 三相変圧器が接続される三相回路はほぼ平衡している。
(2)定格容量
定格二次電圧、定格周波数及び定格力率において規定された温度上昇の限度を超えることなく二次端子間に得られる皮相電力(kVA)を定格容量という。定格力率は、その力率において使用されるよう変圧器が設計された力率をいい、特に指定がないときは100%とされる。
(3)定格周波数
定格周波数は50Hzと60Hzの2種類があるが、兼用器とする場合がある。変圧器の場合、一般的に60Hz専用器は50Hzで使用できないが、50Hz器はインピーダンス電圧が約20%高くなることを考慮すれば60Hzで使用できる。第3表に異なる周波数で使用した場合の特性変化の例を示す。特性変化の値については、変圧器の定格仕様によって異なるため第3表は参考値である。周波数を変更した場合の主な特性変化を考察すると次のようになる。
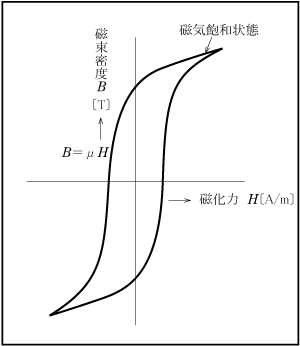
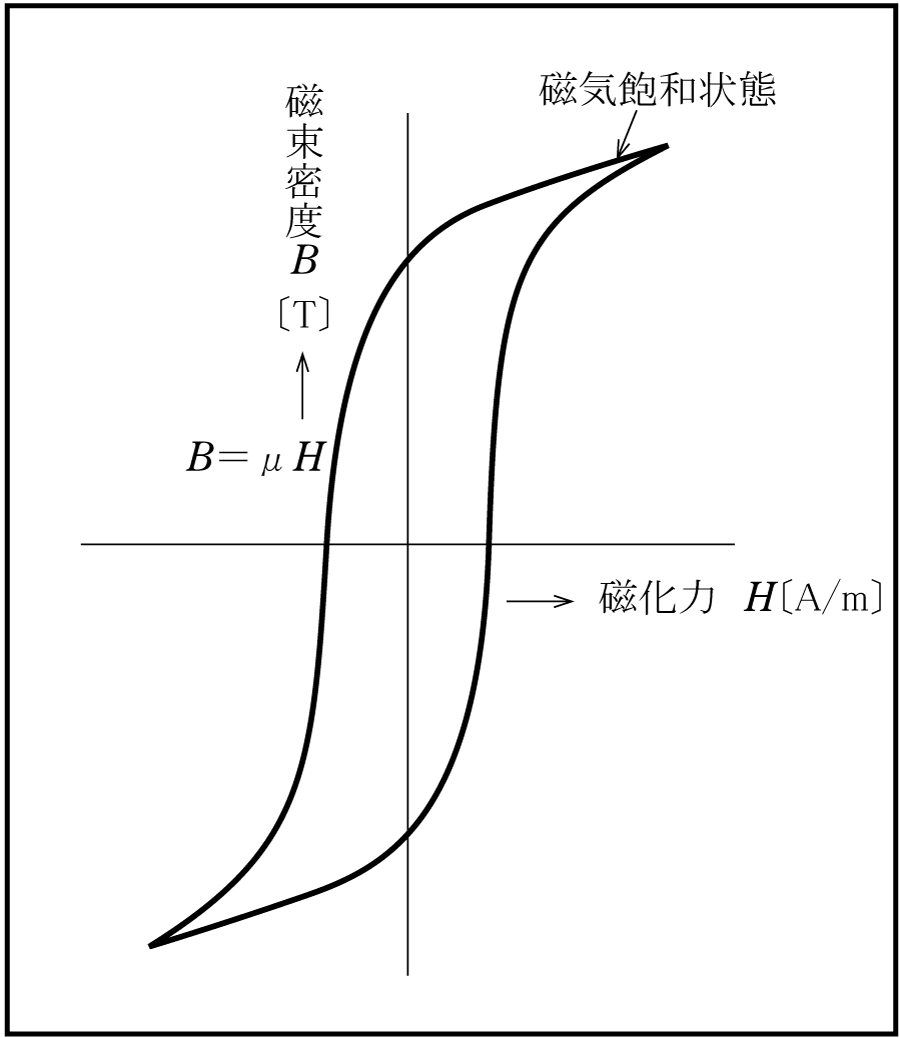
① 鉄損
鉄損ただし、
ただし、
ただし、
ただし、
ただし、
ただし、
ただし、
一次誘導起電力は磁束に対し
ただし、
一次誘導起電力は磁束に対し
これを(2)式に代入すると、ヒステリシス損
したがって、鉄損
② 銅損
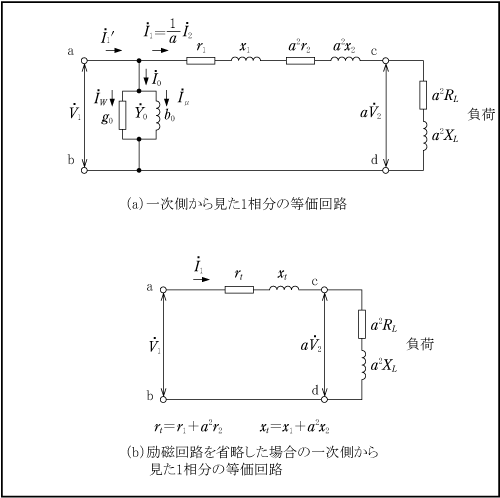
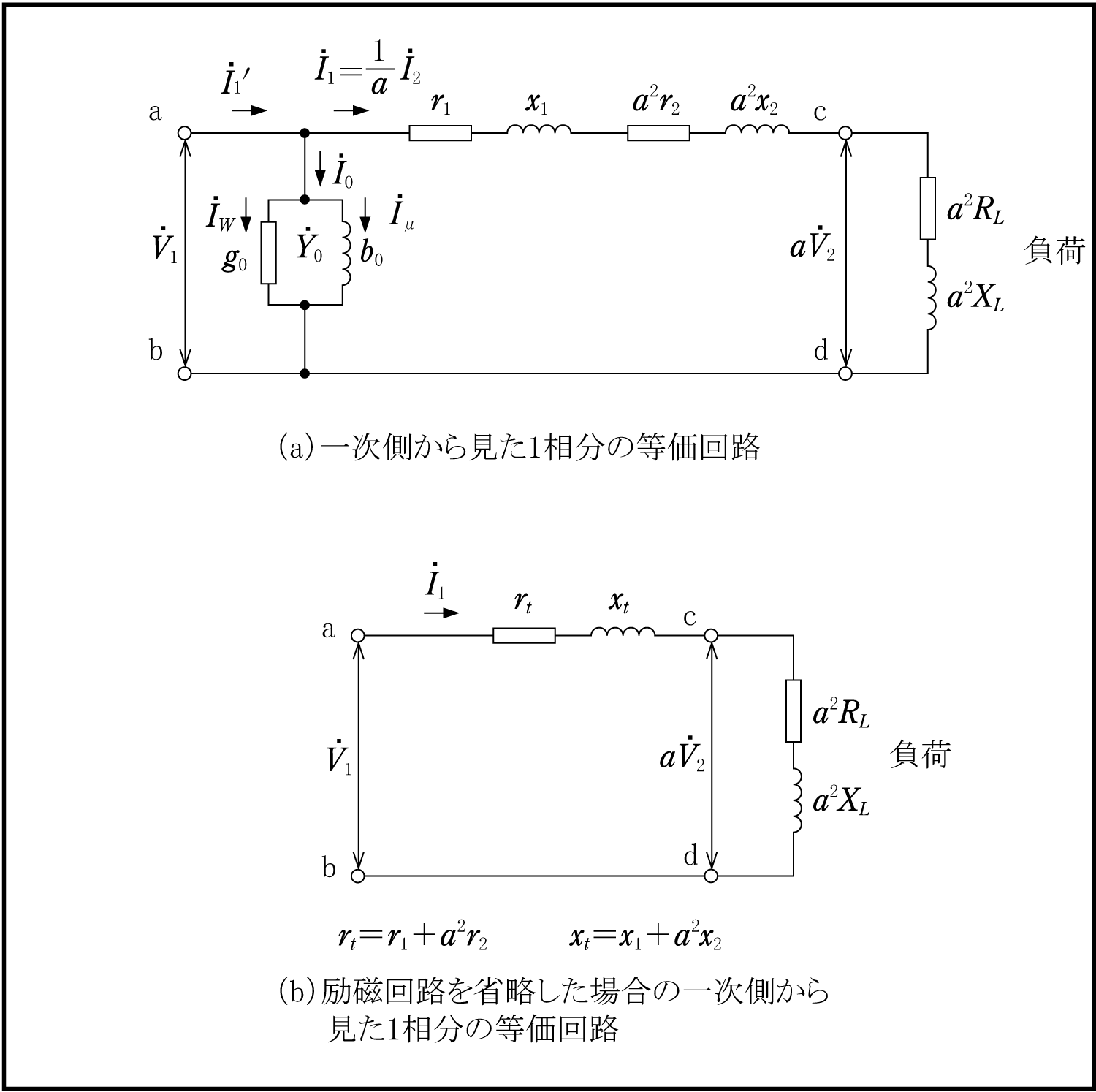
第2図(a)は変圧器と負荷の1相分を一次側に換算した等価回路である。ただし、
銅損
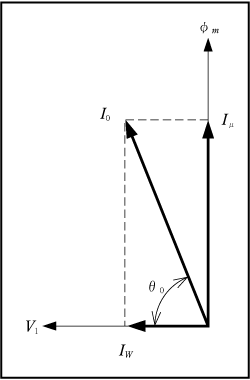
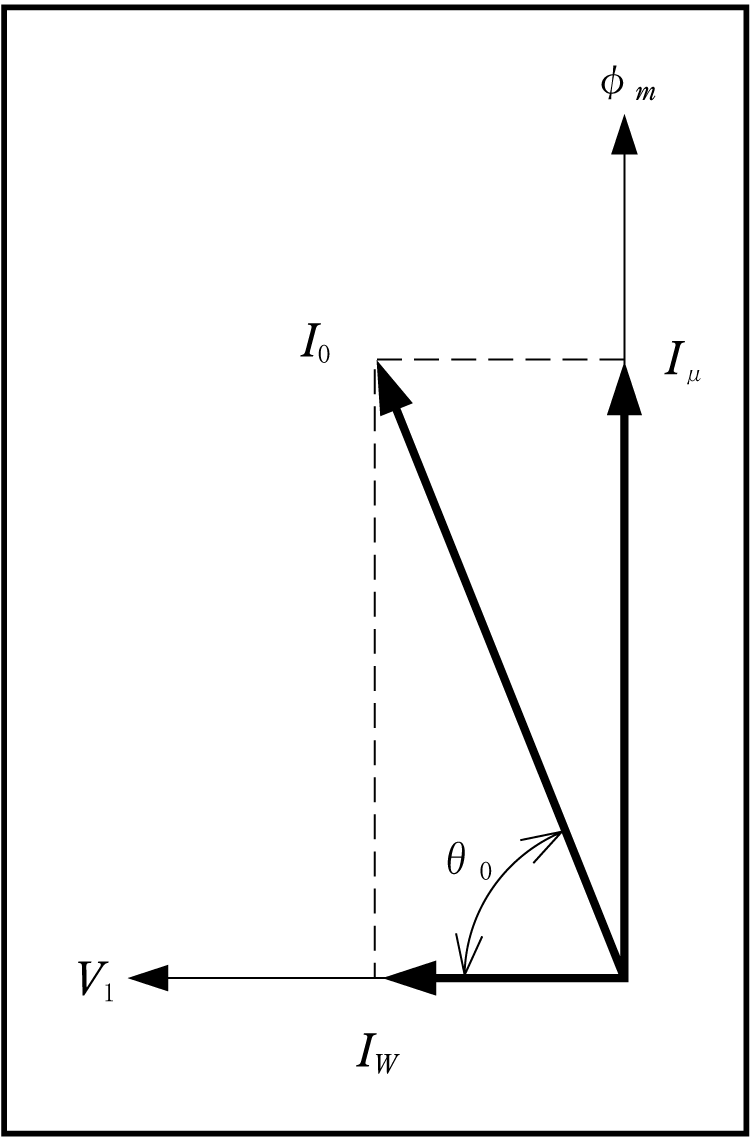
③ 励磁電流
第2図(a)の等価回路において励磁電流ただし、
ただし、
次に自己インダクタンス
ただし、
ただし、
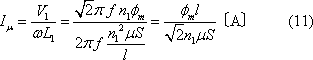
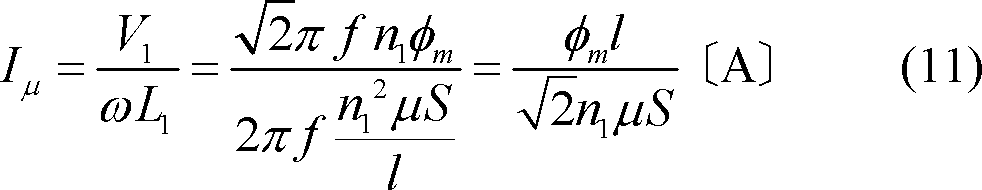
(7)式から周波数が減少すると鉄損が増加し、(12)式から鉄損電流
次に(4)式から一次電圧が同一のとき、周波数
④ インピーダンス電圧
第2図(b)の等価回路において%で表したインピーダンス電圧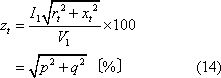
ただし、
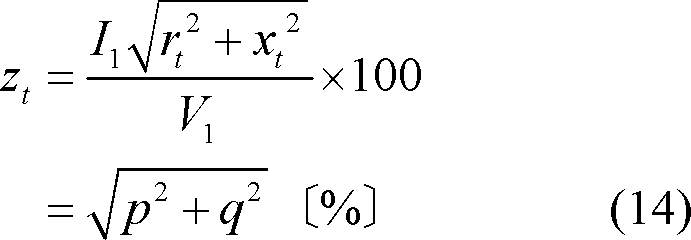
ただし、
(4) 定格電圧
定格電圧は一次側は巻線の基準タップに接続された端子間に印加するために指定した電圧、二次側は無負荷時に発生する電圧であり、共に実効値で表す。定格電圧を一方の巻線に印加したとき無負荷時には他方の巻線に定格電圧が誘起される。(5) タップ電圧
タップは変圧比を変える目的で巻線に設けられた線路端子で、無負荷時に発生または印加される指定電圧をタップ電圧という。タップ電圧には全容量タップ電圧と低減容量タップ電圧がある。全容量タップ電圧は巻線の温度上昇限度を超えることなく定格容量で使用できるタップ電圧であり、Fの記号を付ける。全容量タップ電圧の中で定格電圧を印加する基準タップはRの記号を付ける。低減容量タップ電圧は温度上昇限度を超えることなく使用するためには、定格容量を低減しなければならないタップ電圧であり、記号を付けない。第1図(b)の三相100kVAの場合、一次電圧F6,300Vまでが全容量タップ電圧であり、一次電流の最大値は、
(6) 短絡インピーダンス
短絡インピーダンスは定格周波数で基準タップにおいて、一方の巻線を閉路(短絡)し、他方の巻線側から測定した等価的な星形結線に置き換えた(1相分の)インピーダンスをいう。従来、インピーダンス電圧と称したものが規格改正(1)(2)に伴って呼称が変更されたものである。第2図(b)の等価回路においてはΩ値で表した短絡インピーダンス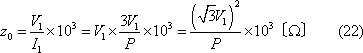
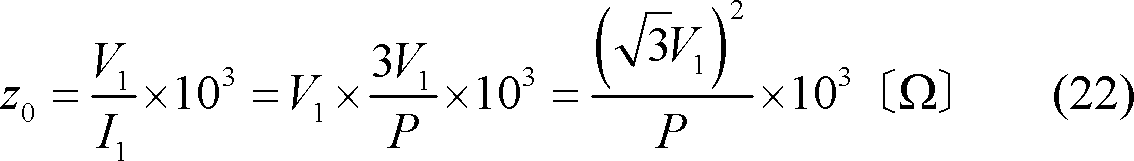
(22)式は(19)式の形式となっている。つまり、基準インピーダンスは定格電圧で定格容量の運転状態において、一次側から負荷側を見た(負荷のインピーダンスを含めた)全インピーダンスを表している。これに対し、短絡インピーダンスは(17)式に示すように変圧器巻線だけのインピーダンスを表す。これを第1図(b)の三相100kVAで試算すると次のようになる。
基準インピーダンス
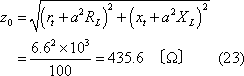
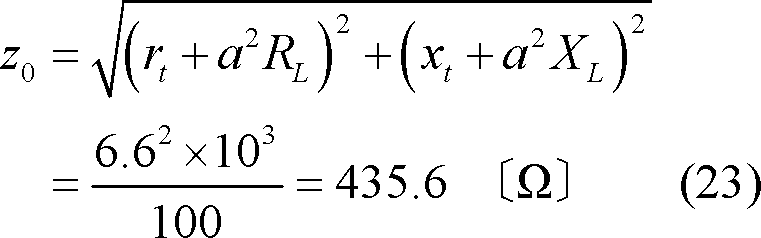
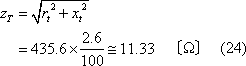
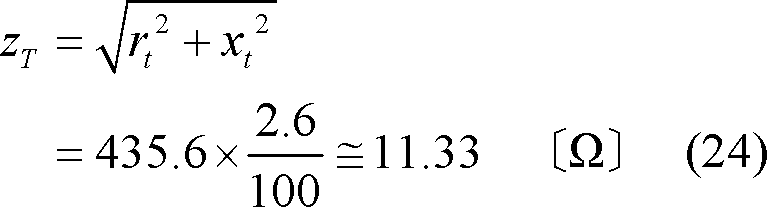
なお、抵抗値は温度によって変化するため、短絡インピーダンスは基準巻線温度に補正した値で表す。温度
(7) 定格二次電流
定格二次電流は、定格容量と定格二次電圧から算出される線路電流の実効値であり、第1図(a)の単相100kVAでは次のように算出される。(8) 巻線の温度上昇
巻線の温度上昇は変圧器を定格容量で連続運転し、巻線の温度上昇が最高となったときの周囲温度との差をもって定め、単位は〔K〕(ケルビン)を使用する。巻線の最高温度ただし、
ただし、
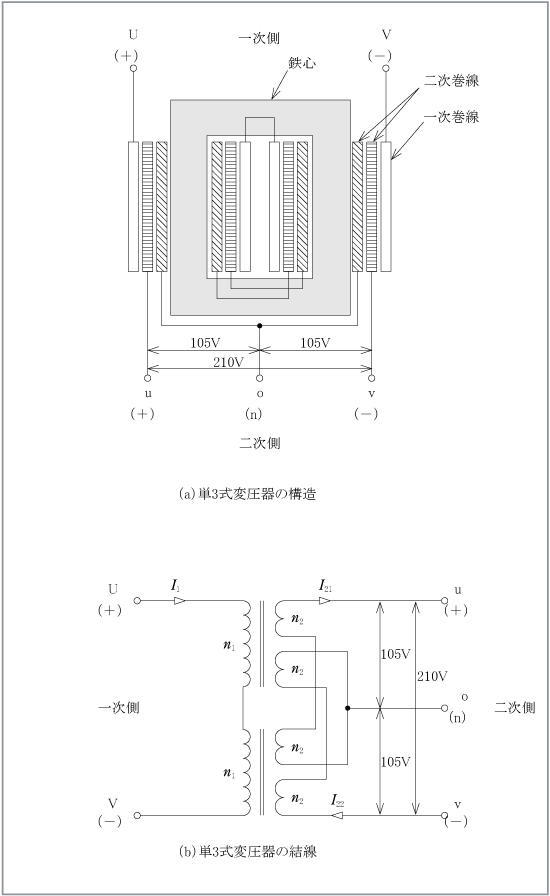
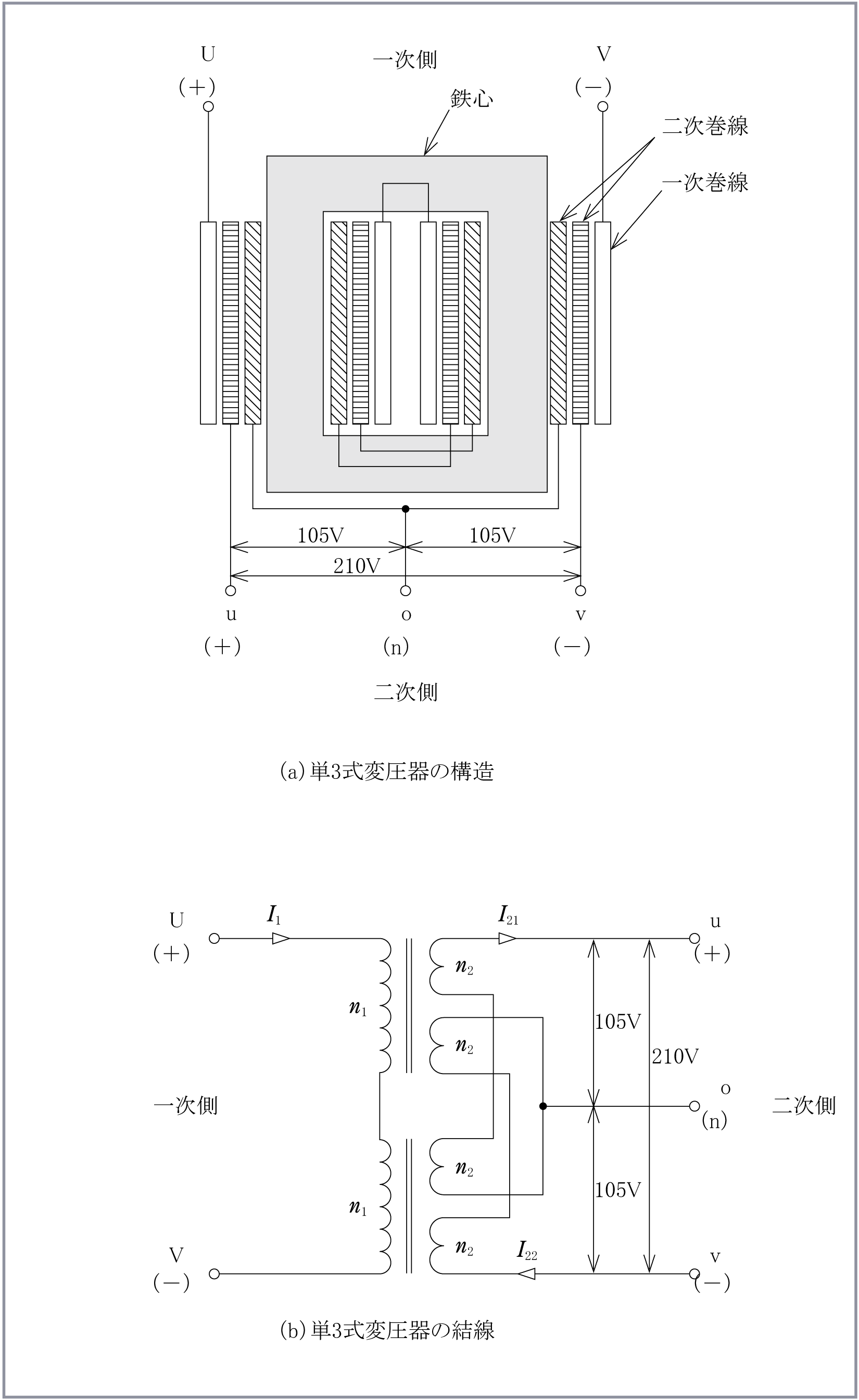
(9) 結線図
第5図は単相3線式変圧器の構造と結線を表したものである。二次側結線は単3結線を標準とし、第5図(b)に示すように低圧巻線を2分割し交差接続する。これは105V回路の負荷が不平衡になっても、一次巻線と二次巻線のAT(アンペアターン)が過不足となってインピーダンスの増加を招かないようにするためである。各鉄心の脚ごとに次の式が成り立つ。
ただし、
ただし、
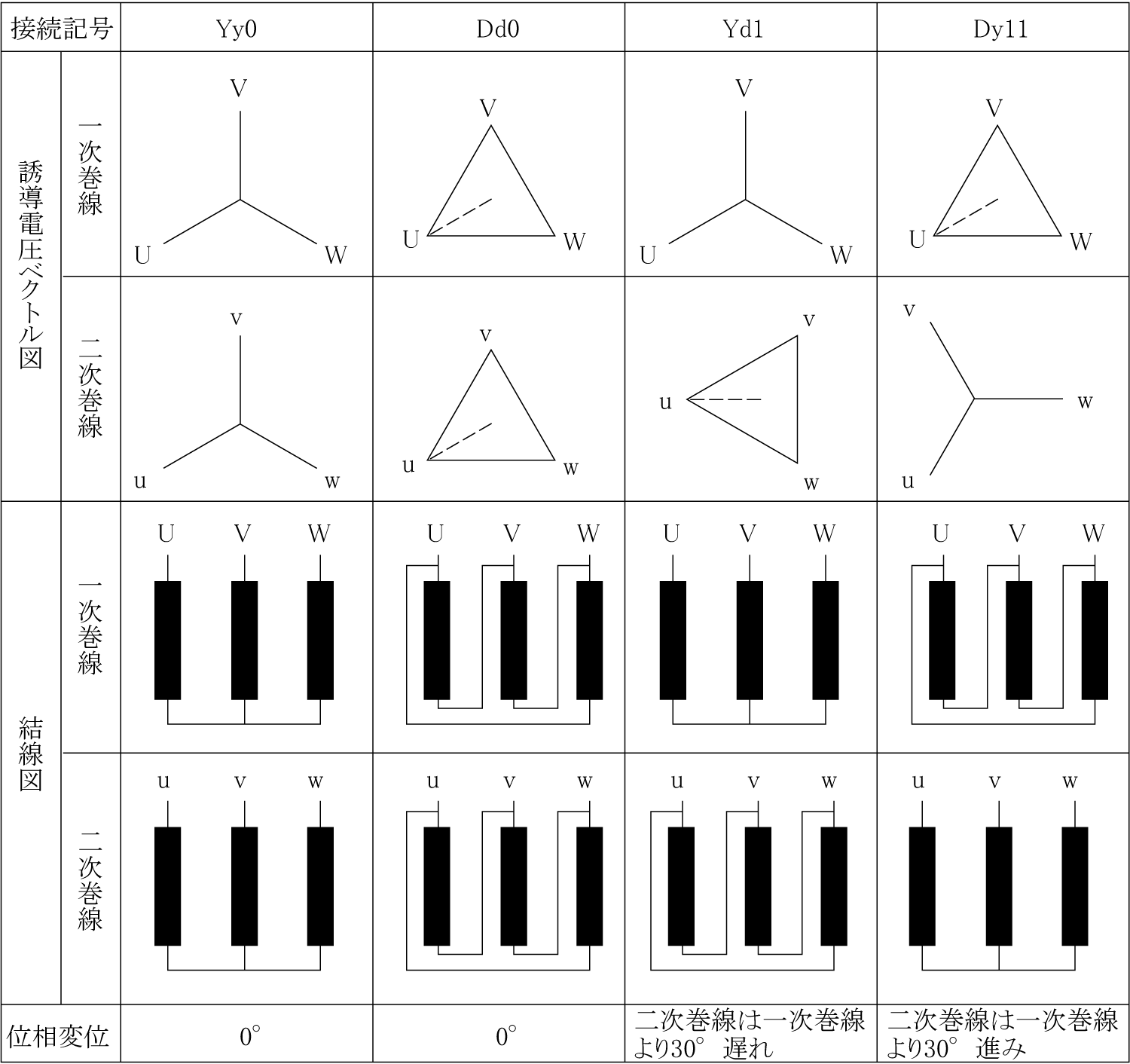
三相変圧器の一次結線及び二次結線は星形結線と三角結線がある。三相変圧器の結線の組み合わせと位相の変位は第4表のようになる。
参 考 文 献
〜終わり〜
■ぜひアンケートにご協力下さい■