〜終わり〜
■ぜひアンケートにご協力下さい■
ベクトル制御の解説書に頻繁に出てくるdq変換と関連技術について易しく解説する。今回は電動機のベクトル制御の基礎2で説明した二相変換を座標軸を統一したdq変換した誘導機について解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
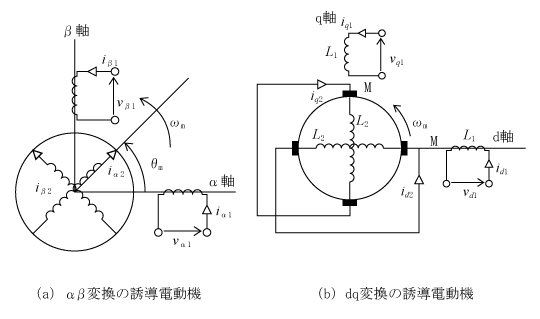
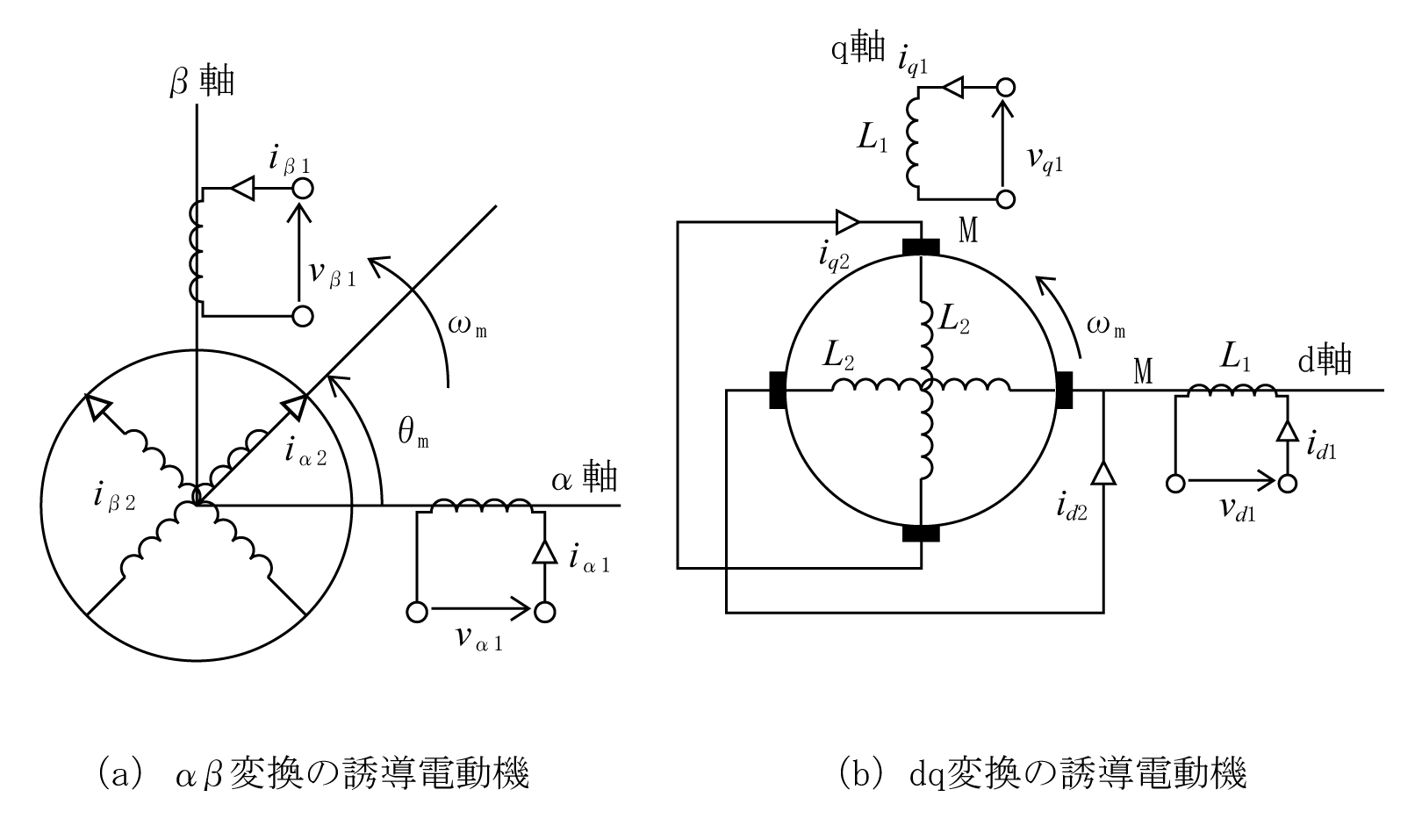
電動機ベクトル制御の基礎2で説明した二相変換では、第1図（a）（電動機ベクトル制御の基礎2 第3図（b）を再掲）のように固定子と回転子がそれぞれに独自の座標系であった。ここで両者の座標軸を統一する。第1図（b）はdq変換した誘導機である。
第1図（a）の回転子のα2β2座標系を時計方向にθmの回転を行い固定子の座標系に合わせると第1図（b）になる。回転方向が時計回りなので、変換行列は順方向変換行列の「θm」を「－θm」にするか、転置行列によって以下の行列になる。
（1）
（1）
一次巻線（固定子）については、回転変換が不要なので、α1β1系の式がそのままdq軸の式になって[dqi1]=[αβi1]、[dqv1]= [αβv1]である。
二次巻線（回転子）の電圧・電流方程式を[dqCαβ]の変換行列を作用させて求める。
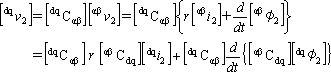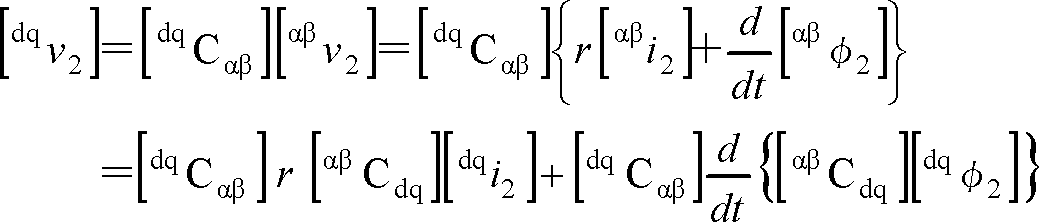（2）
（2）
第2項は時間微分を含んだ座標変換であり公式化した。しかし、ここでは逆向きの回転変換なので（公式B）を使用すると、第2項=－(ωmJ－P)[dqφ2]である。
dq座標系の電圧方程式を一次巻線の式と共にまとめると、
（3）
（3）
となる。これを行列要素で表す。
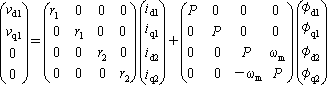
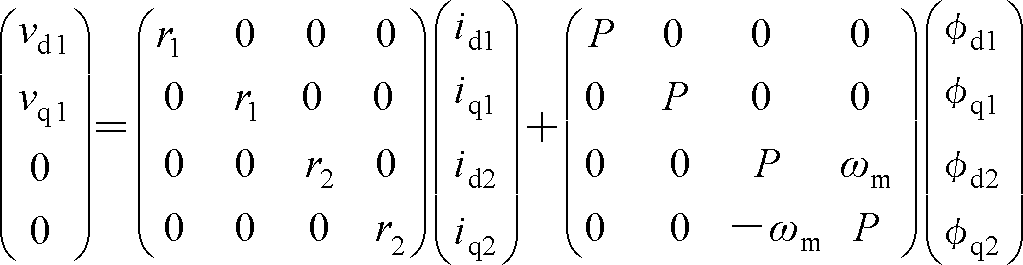
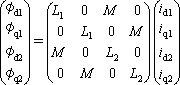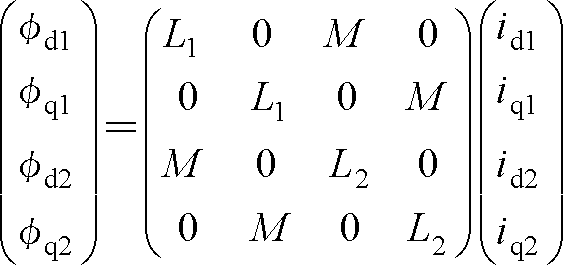（4）
（4）
ここで、d、q軸が直交しているので、φd1、φd2にはそれぞれi q1、i q2の要素がなく、該当の行列要素はゼロである。また、φq1、φq2にはi d1、i d2の要素がゼロになっている。
これまでの変換過程を式で表すと[dqCαβ][αβCabc]=[dqCabc]である。よく技術文献では「dq変換」としていきなり出てくる変換である。ここでθmをθに置き換えてdq変換行列を計算しておく。
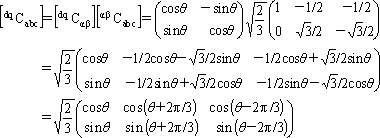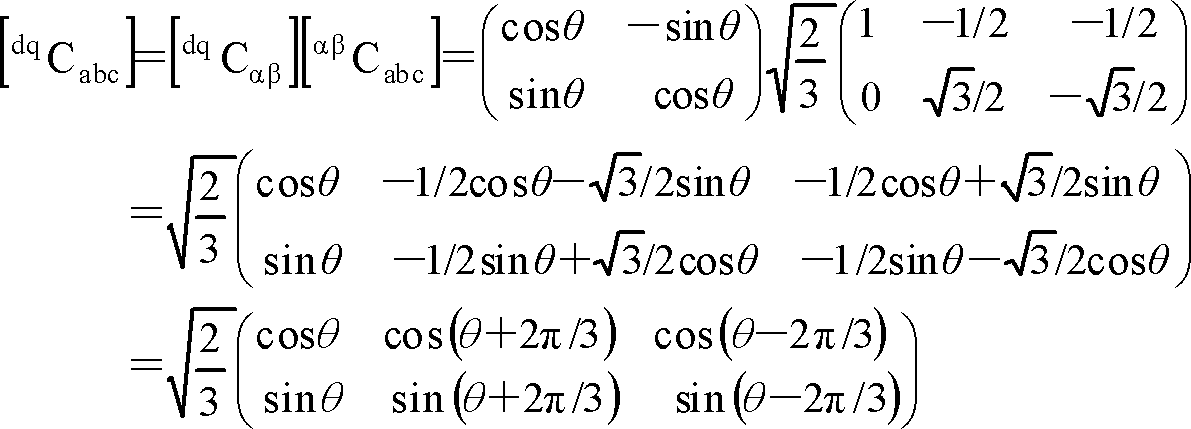（5）
（5）
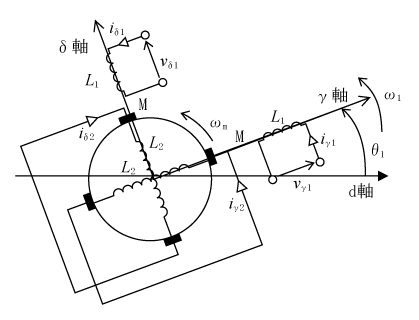
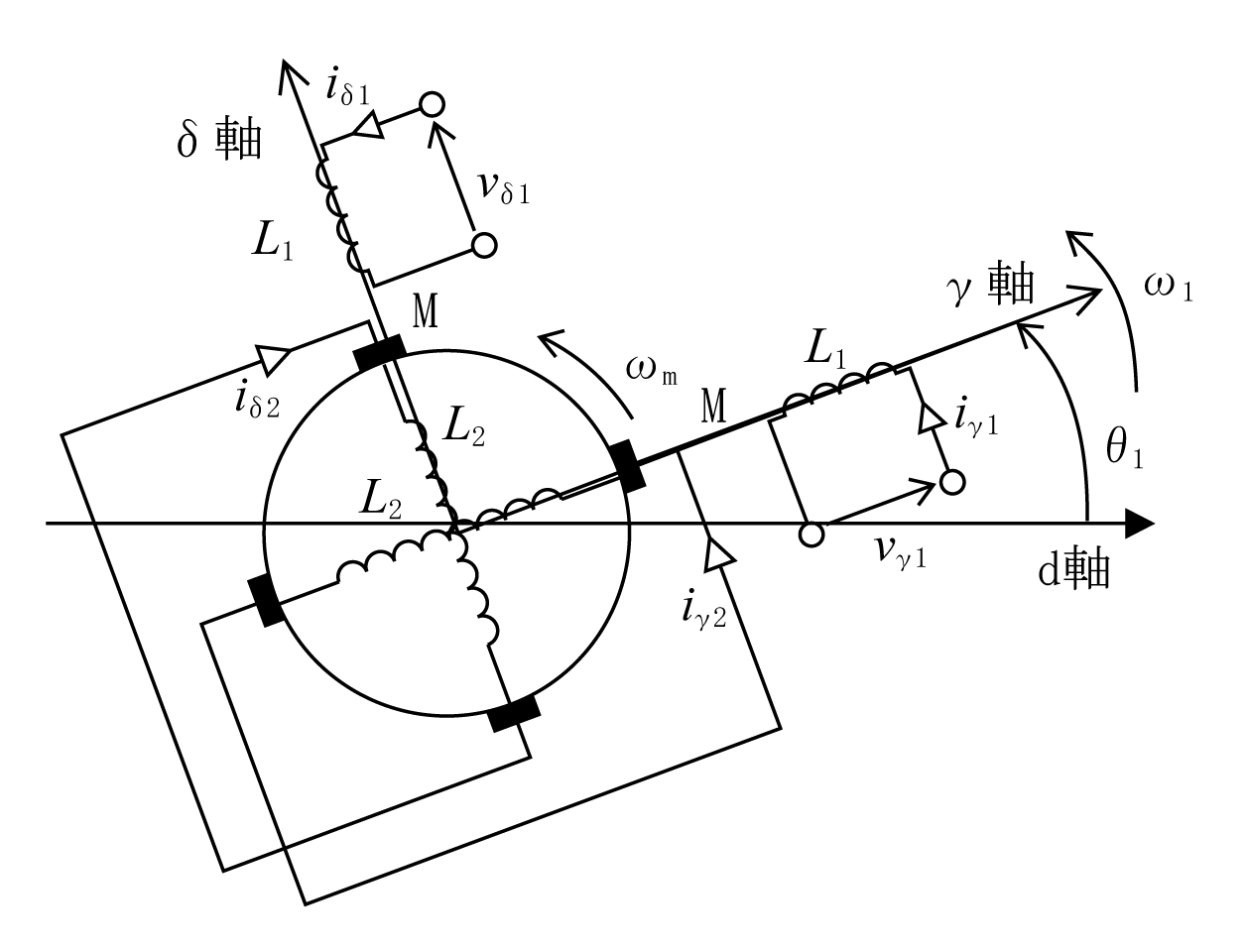
第2図はdq変換で一つになった軸系を位置（角度）がθ1で回転角速度ω1（=2π f1 f1:電流の周波数）の座標に変換する。すなわち、回転磁界上の座標系であり、この変換をγδ座標系という。
回転磁界から回転子をみると滑り周波数で回転して見えるので、この変換には滑り周波数（ωs）が現れる。滑り周波数を含んだ解析に都合のよい変換である。
変換行列は回転が反時計回りなので角度θ1の順回転変換である。
（6）
（6）
dq座標系の（3）式に変換行列を掛けて電圧方程式を求める。
一次巻線（固定子）については順方向の回転変換の（公式A）を使う。
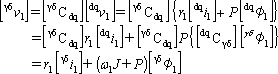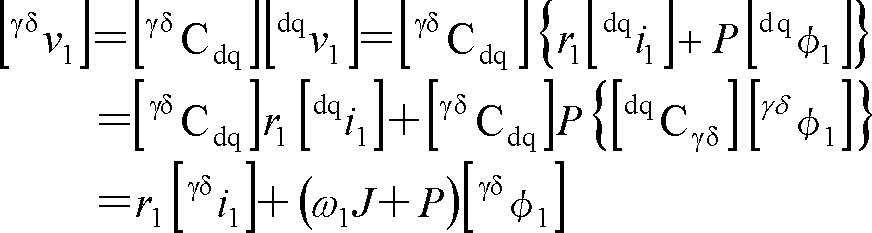（7）
（7）
二次巻線（回転子）はやや複雑になるが、同じく（公式A）を使って計算する。
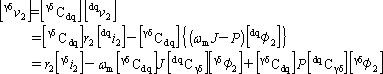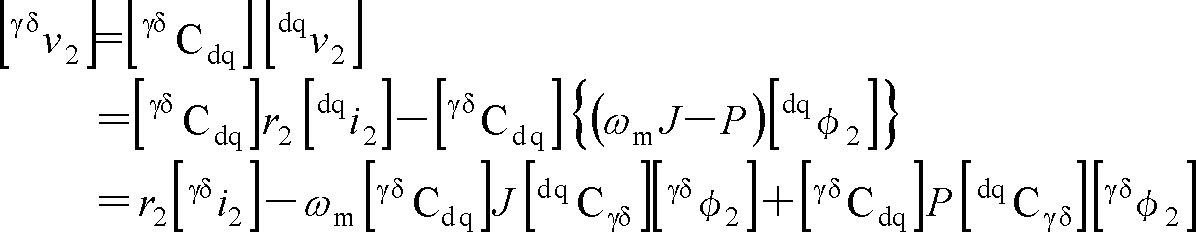（8）
（8）
第2項の[γδCdq] J [dqCγδ]は行列計算を実行するとJになる。第3項は回転変換の公式から、（ω1J＋P）[γδφ2]である。
以上をまとめると、
（9）
（9）
である。ωs=ω1－ωmの関係を入れて（7）、（9）式を行列要素で表現する。
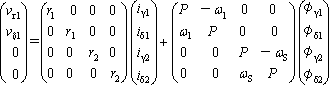
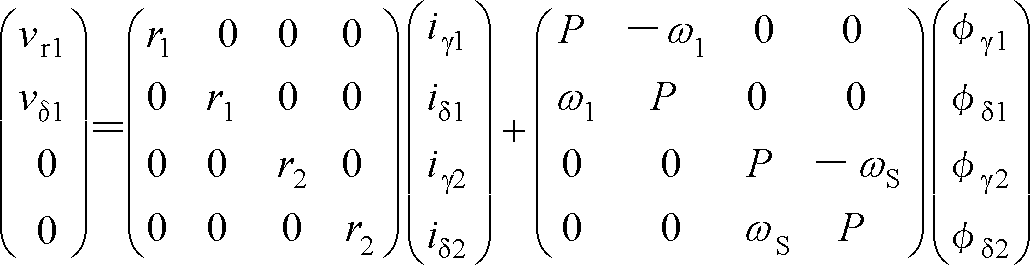
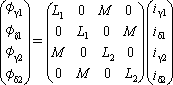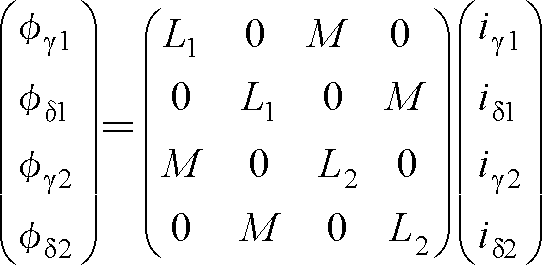（10）
（10）
行列要素に滑り角速度ωsが現れているところがポイントである。
dq座標系の電圧・電流方程式をベクトルで表現することについて考える。
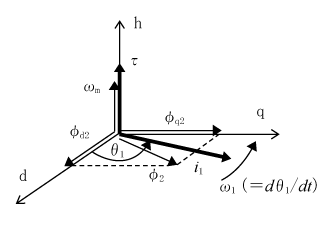
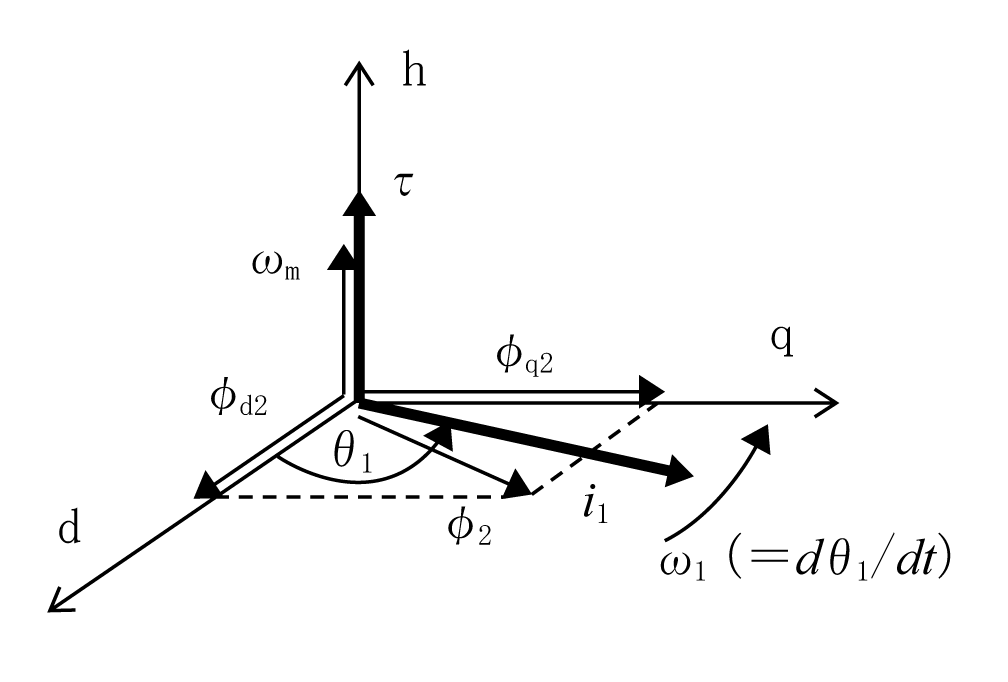
右ねじ系の三次元ベクトル空間として、dq平面に直角方向をh軸とする。この座標系に第2図のδγ変換した諸量を第3図のようにベクトルで配置する。v1、i1、i2、φ1、φ2はdq平面を回転するが、回転角速度ωmとトルクτはh軸方向のベクトルになる。
dq変換した電圧方程式（4）はベクトルv1、i1、i2、φ1、φ2で次式のように表現される。
（11）
（11）
対応が見えにくい「－ωm×φ2」の要素について確認する。これを行列に書き替える。
（12）
（12）
第3図のφ2とφd2、φq2を参照してベクトル積の向きを求めると、－ωm×φd2はq軸のマイナス方向のベクトルになり、－ωm×φq2はd軸のプラス方向のベクトルになる。すなわち、以下の式が成立する。
（13）
（13）
これは（4）式の電圧方程式の該当要素を再現している。すなわち、（11）式は（4）式と等価である。（13）式は更に、
（14）
（14）
になる。（11）式の対象部分を比較すると「×」と「J」が対応している。すなわち、「J」は行列に、「×」はベクトルでの表現といえる。
トルクは、磁界（φ2）と電機子電流（i2）についてフレミングの左手の法則（力=電流×磁界）に従う。ここで、極対数を小文字のpとするとトルクは、
（15）
（15）
である。
ベクトル制御は誘導電動機の一次電流を磁束をつくる成分とトルクを発生する成分に分解し、それらの成分を互いに独立に制御する方法である。代表的例として、「φ2一定制御」について説明する。
トルクτ=pi2×φ2を制御するために外部から直接検出して制御できるのは一次電流ベクトルi1だけである。そこでφ2を一定に制御するためにi1をdq座標でどのように制御すればよいかになる。
二次巻線（回転子）の電圧方程式（9）式で二次巻線の電圧がゼロを考慮し、「J」を「×」に置き換えてベクトル表示すると次式になる。
（16）
（16）
φ2一定制御の条件では、Pφ2=0であり、これを代入してi2について解くと、
（17）
（17）
になる。この式からi2、ωs、φ2はベクトル積の関係なので、互いに直交しているベクトルである。
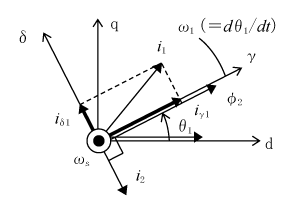
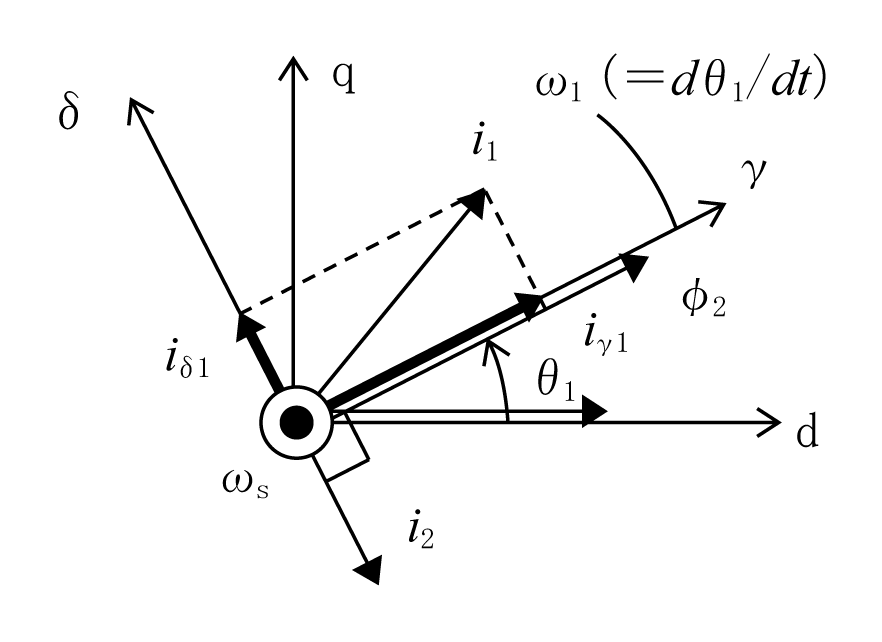
第4図のように二次磁束ベクトルφ2の方向にγ軸をとり、これと直交方向にδ軸として座標系を設定する。これからφ2のδ、γ要素はφγ2=φ2で、直交位置にあるのでφδ2=0である。また、（17）式から、i2はωs、φに直交した配置になる。
図にi1を加え、そのγ、δ軸の成分をそれぞれiγ1、iδ1とする。
（18）
（18）
また、磁束φ2は、（11）式からMi1+L2i2であり、また第4図からiγ1と同相なのでMを使ってMiγ1でもある。したがって、次式が成り立つ。
（19）
（19）
iγ1はこのようにφ2を決定するのでi1の「磁束電流ベクトル」といわれる。
（18）式と（19）式からi1を消去すると、
（20）
（20）
が得られる。したがって、トルクτは次式のように計算される。
（21）
（21）
式の途中で外積の順序を変えた。iδ1は（21）式でトルクを設定するので、i1の「トルク電流ベクトル」と呼ぶ。
前述のiγ1、iδ1は直流電動機の界磁電流ベクトルと電機子電流ベクトルにおのおの対応しており、電動機のトルクを設定する。
iγ1、iδ1を実際に外部から制御するには、γδ座標系からdq座標系に変換する二次鎖交磁束方向（γ軸の方向）θ1が必要になる。その方法としてギャップに磁束検出用の磁気センサを配置して直接計量するか、またはなんらかの方法で間接的に推量することになる。
例えば、二次磁束φ2が一定の場合は、滑り周波数ωsが（17）式と（19）、（20）式から、
（22）
（22）
で求められる。そこでモータの回転数速度ωmを検出すれば、ωm＋ωs=ω1によりω1が求まり、これを時間積分してθ1を推量できる。
このようにωsから推量するベクトル制御を滑り周波数形のベクトル制御という。
（1） 電気学会 交流電動機駆動方式の技術・分類・用語整理調査専門委員会編:交流電動機可変速駆動の基礎と応用、コロナ社刊
（2） インバータドライブハンドブック編集委員会編:インバータドライブハンドブック、日刊工業新聞社刊
（3） 片岡昭雄:電動機の可変速駆動入門、森北出版株式会社刊
（4） 赤木泰文:ACモータのベクトル制御、電学論D 108巻8号、1988