〜終わり〜
■ぜひアンケートにご協力下さい■
ベクトル制御の解説書に頻繁に出てくるdq変換と関連技術について易しく解説する。今回はαβ軸をθ度回転し、回転した座標系をここではxy軸座標系とするなど、回転座標変換について解説する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
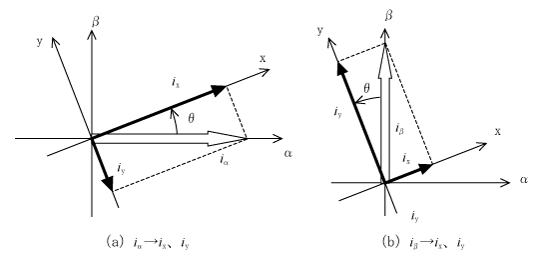
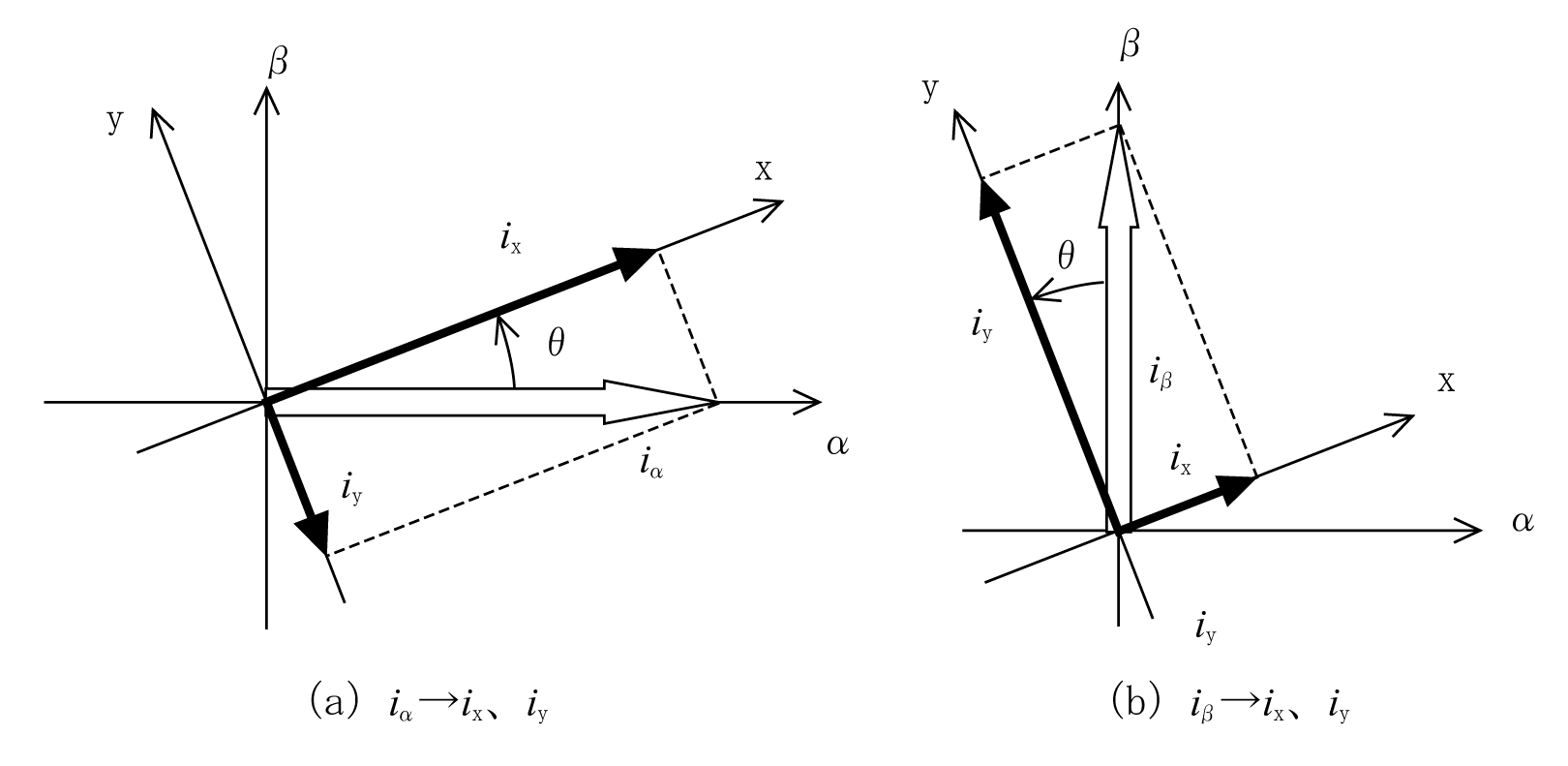
第1図のようにαβ軸をθ度回転し、回転した座標系をここではxy軸座標系とする。
αβ軸系での電流iα、iβがθ回転したxy軸からはどのように見えるだろうか。
α軸の方向にiαの電流をxy座標系から眺めるとx方向にiαcosθが流れ、y方向には－iαsinθが流れて見える。同様にβ軸方向にiβの電流はx方向にiβsinθ、y方向にはiβcosθが流れて見える。まとめると、αβ座標系で（iα , iβ）の電流はxy座標系では、
（1）
（1）
となっている。これを行列で表すと、
（2）
（2）
である。これは（iα , iβ）をθ回転した（ix , iy）への変換なので、
（3）
（3）
が変換行列である。また、逆変換は[xyCαβ]－1=[xyCαβ]Tが成立して次式になる。
（4）
（4）
逆方向回転変換は回転方向が逆とみなして、「θ」に「－θ」を代入して得られる。回転座標変換のポイントは、座標軸の回転の順と逆を見分けることにある。例の回転はx軸からy軸に向かう反時計回りであり、この方向が順回転である。
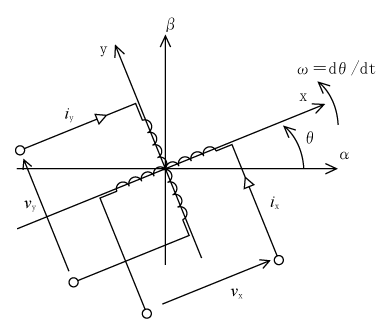
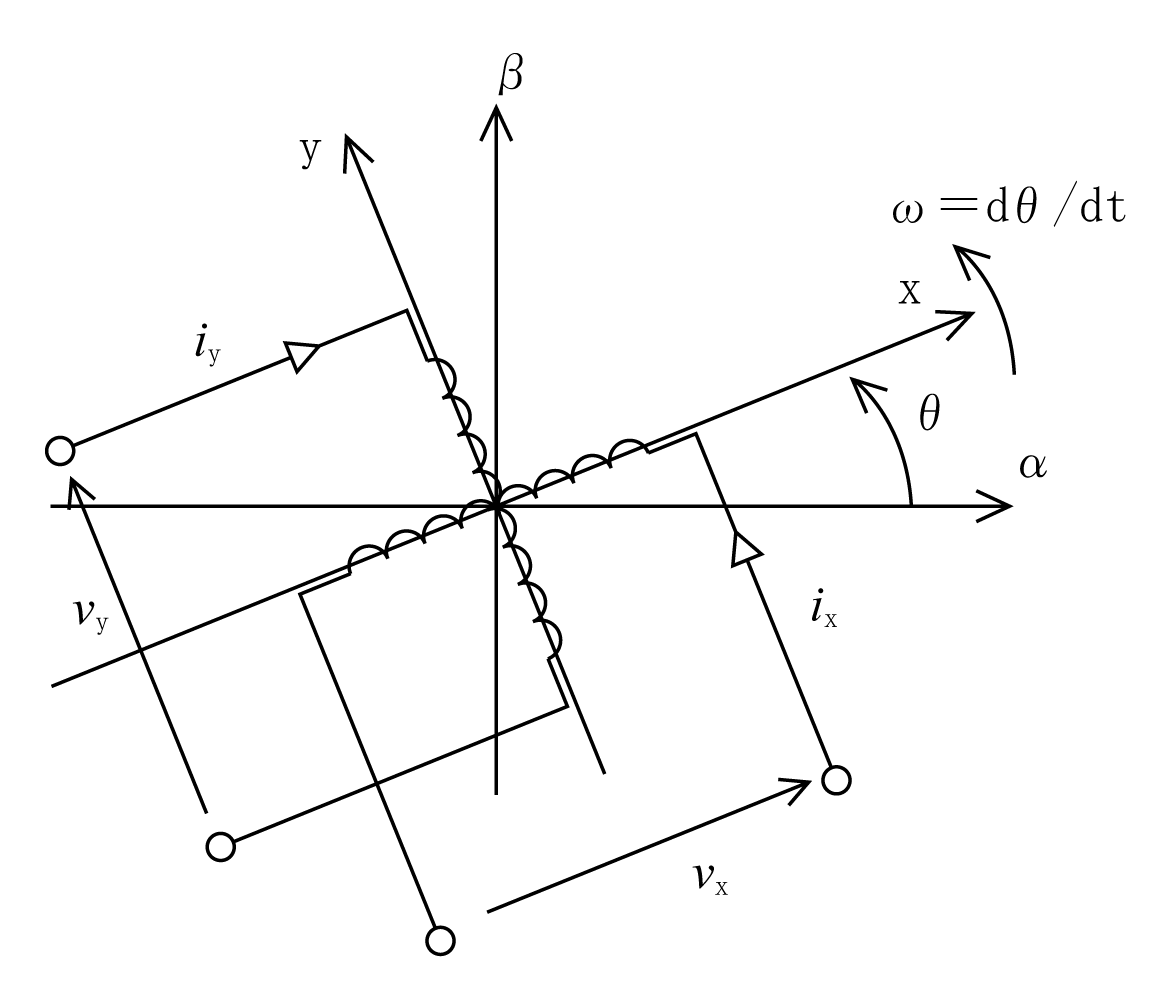
第2図のように角速度ωで回転している二相巻線について考える。誘導電動機の回転子のイメージになる。ここで回転速度ω=dθ/dtとする。
回転方向がα軸からβ軸方向に反時計回りなので、順方向変換である。
二相に変換された電圧方程式を回転座標変換する。左から変換行列を掛ける。
（5）
（5）
（5）式の第1項はr [ xyi ]になるが、第2項の微分に注意が必要である。
変換行列はθの関数で軸が回転しているので時間tの関数である。したがって、行列の積をtで微分することになる。行列の積の微分公式は、
（6）
（6）
で、1個づつ微分する。公式を使って微分すると、
（7）
（7）
となる。変換行列を直接tで微分できないのでθを介して行うと、
（8）
（8）
のように微分計算される。これから、
（9）
になる。まとめると（5）式第2項は、
（10）
ただし、
になる。なんとなく、電気屋になじみのωJが出てきた。まったく無関係とはいえないらしい。
ここで横道にそれるが、（10）式は今後も出現するので計算結果を公式化しておく。
順方向の回転変換[C]の場合、
（公式A）
逆方向の回転変換の場合は、「θ」に「－θ」を代入することで算出できる。
なので公式Aのωを－ωに変換することで、逆方向の回転では次の公式になる。
逆方向の回転変換[C] Tの場合、
（公式B）
元に戻る。d/dt = Pの演算子を使うと（5）式の電圧方程式は、
（11）
（11）
になる。
また、磁束については回転変換によってインダクタンスは変わらないので[αβL]=[xyL]=Lとして、
（12）
（12）
となる。
以上から、順方向の転換座標系の電圧方程式は、
（13）
（13）
で行列要素表示では、
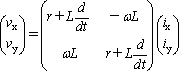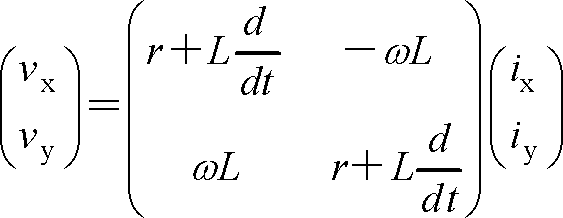（14）
（14）
である。非対角要素としてωLが現れる。これは、角速度ωに比例しており速度起電力と呼ばれる。PM同期モータでは盛んに出てくる用語の一つである。
巻線が1個の場合を例として、座標変換によりどのように簡単化され、変化していくかを変換の展開に沿って説明してきた。
次は誘導電動機のように相互に関係のある2個の巻線へ展開する。
三相誘導電動機の二相巻線表現について解説する。
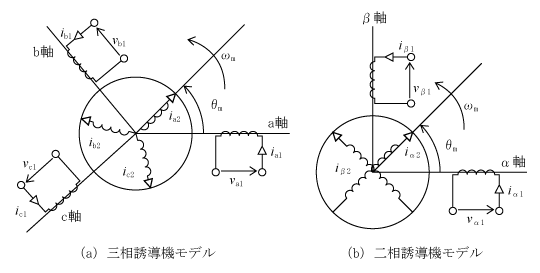
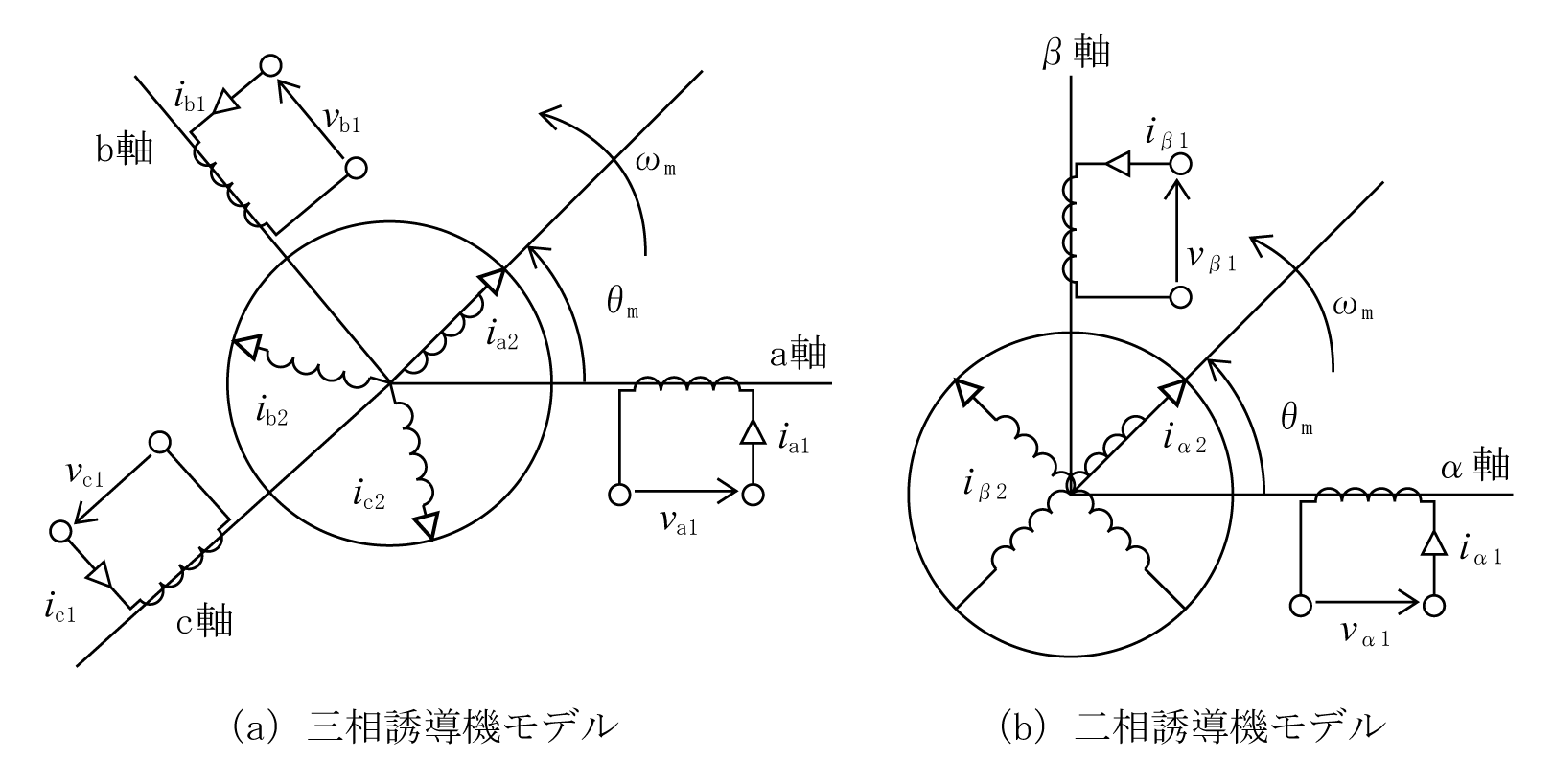
第3図は角速度ωmで運転されている誘導電動機の三相と二相のモデル図で、サフィックスの1と2は、一次及び二次巻線を示している。
第3図（a）は三相モデルで、基準軸を一次巻線のa軸（U相）にとり、そのほかの固定子巻線に対応してb軸（V相）、c軸（W相）の3軸とする。回転子についてもサフィックス「2」を付けて同様に軸名称と基準軸を設定する。
一次巻線の交流電圧・電流の周波数をf1とし、回転子は固定子の基準軸からθmの位置にあり、回転周波数fm（=ωm / 2π）で回転している。
三相モデルの電圧方程式では、各軸で電圧〔va1，vb1，vc1，0，0，0〕T、電流〔ia1，ib1，ic1，ia2，ib2，ic2〕T及び磁束〔φa1，φb1，φc1，φa2，φb2，φc2〕T（〔 〕Tは転置行列を示す）が変数となり、これに6行6列のインピーダンス行列がつくという大変な式になってしまう（式を省略）。
第3図（b）はこれを三相二相変換で、二相誘導機にしたものである。
三相誘導機から二相誘導機への電圧・電流は変換行列〔αβCabc〕を使って、
（15）
（15）
になる。
（16）式に電圧と電流の関係を行列で表した。誘導電動機の二次巻線は短絡されているので、vα2=0、vβ2=0 である。
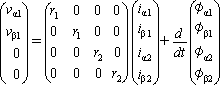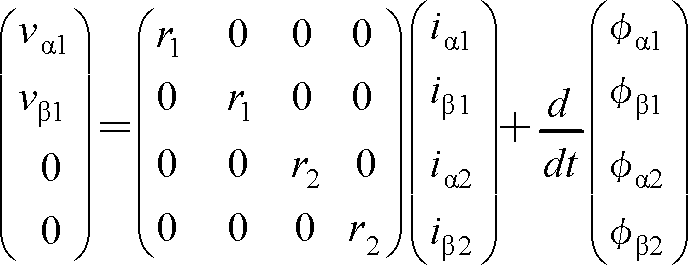（16）
（16）
ただし、r1、r2は一次二次巻線の抵抗値である。
磁束をα軸、β軸の各成分に分解する。一次巻線と二次巻線間の角度がθmなので、
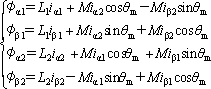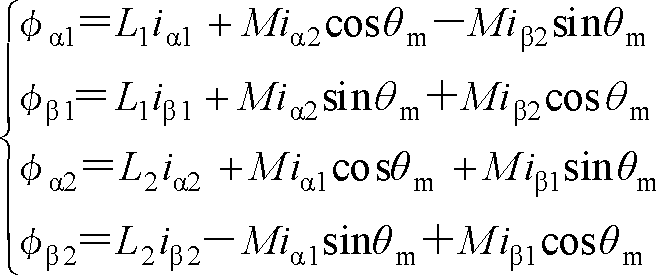（17）
（17）
である。ここで、Mは相互インダクタンスL1、L2は巻線のインダクタンスで漏れインダクタンスは省略した。
全体をまとめて行列表現すると（18）式になり、行列が4行に簡略化されている。
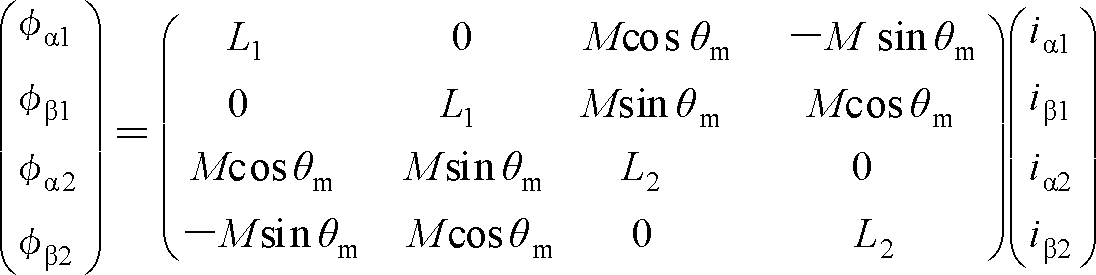（18）
（18）
三相誘導機の6行6列の行列に比べて大きく簡素化されている。
（1） 電気学会 交流電動機駆動方式の技術・分類・用語整理調査専門委員会編:交流電動機可変速駆動の基礎と応用、コロナ社刊
（2） インバータドライブハンドブック編集委員会編:インバータドライブハンドブック、日刊工業新聞社刊