〜終わり〜
■ぜひアンケートにご協力下さい■


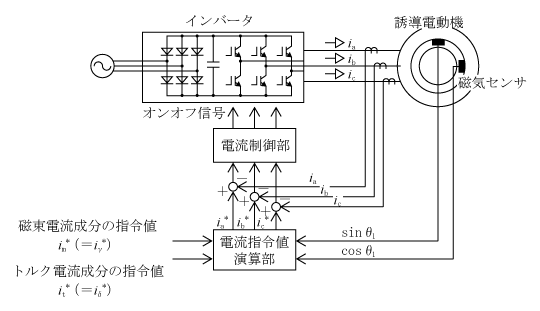
(1)磁気センサ付きベクトル制御(直接型)
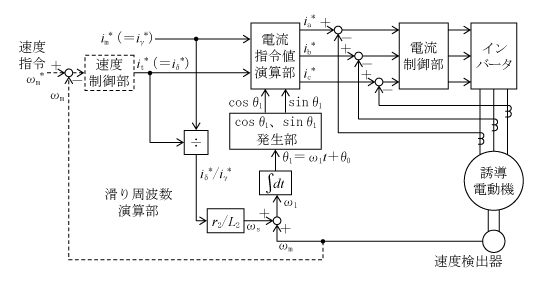
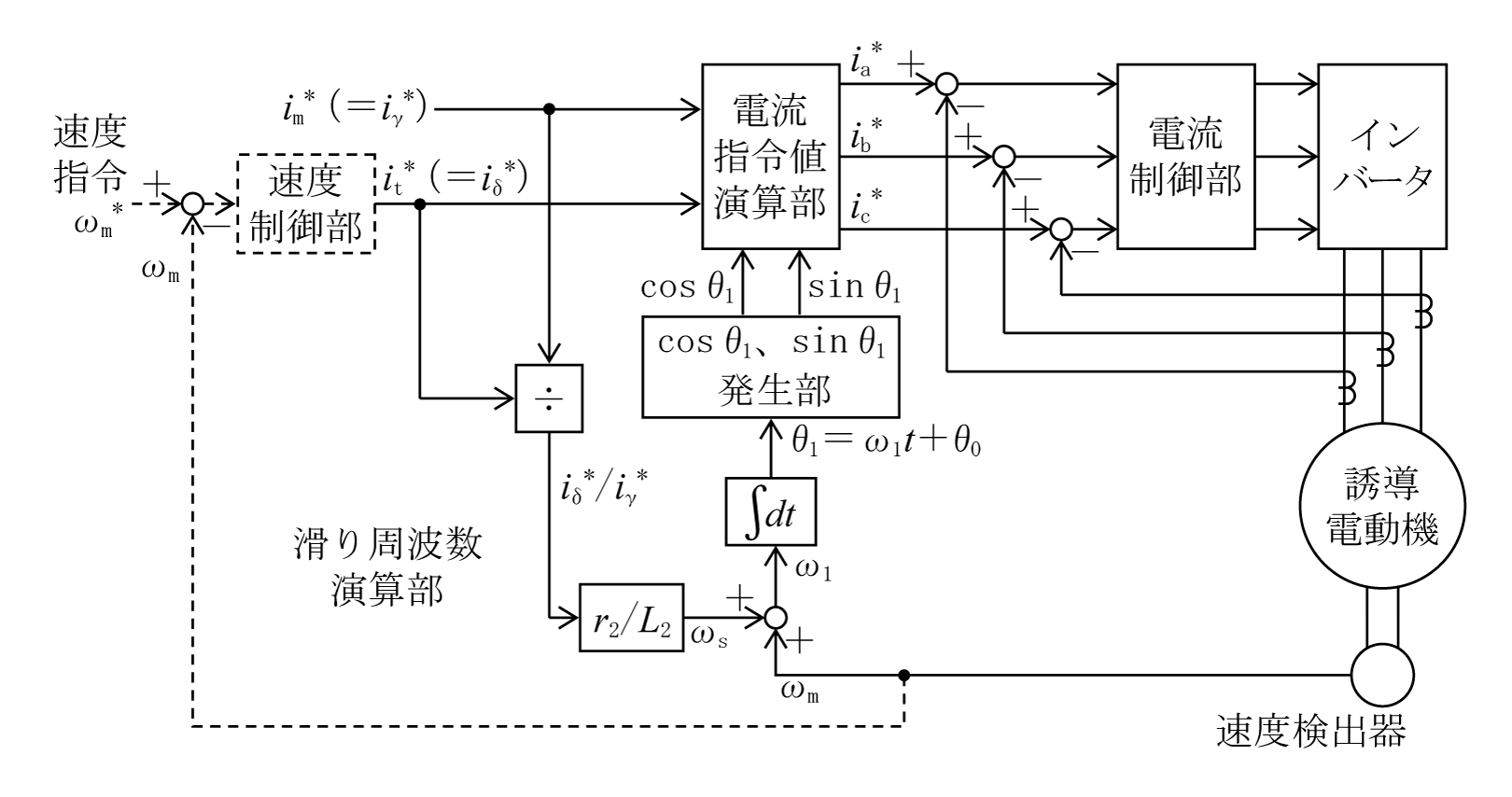
システム構成はいろいろあり、現在も改善や新規考案が進んでいる。導入として第1図のセンサ付きベクトル制御を解説する。
磁束電流成分im*(=iγ*)とトルク電流成分it*(=iδ*)を指令値として与え、これに対応する三相電流ia*、ib*、ic*に座標変換してインバータから誘導電動機に供給している。「*」は指令値を意味し、外部または制御により指定する値である。2個の磁気センサはπ /2[rad]の角度を隔てて誘導電動機の固定子ギャップ面に組み込まれている。そのためセンサの信号は直接cosθ1とsinθ1になる。
電流指令値演算部ではim*(=iγ*)とit*(=iδ*)の指令値と磁気センサからの回転角θ1を入力として、ia*、ib*、ic*を演算する。
ここで、iγ、iδは前回の4で説明したγδ座標系の要素で、これをdq座標系へ逆変換することになる。しかし、一次巻線にとっては、dq座標系はαβ座標系と同じなので、id*=iα*、iq*=iβ*として扱える。すなわち、[dqCγδ]=[αβCγδ]である。これを二相三相変換して、ia*、ib*、ic*を得る。以上を変換式で書くと次の式になる。
この変換の行列要素を計算する。
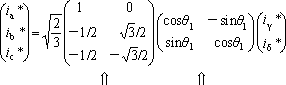
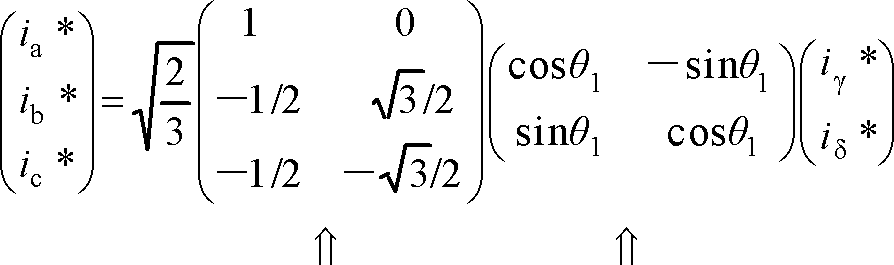
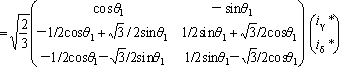 (2)
(2)
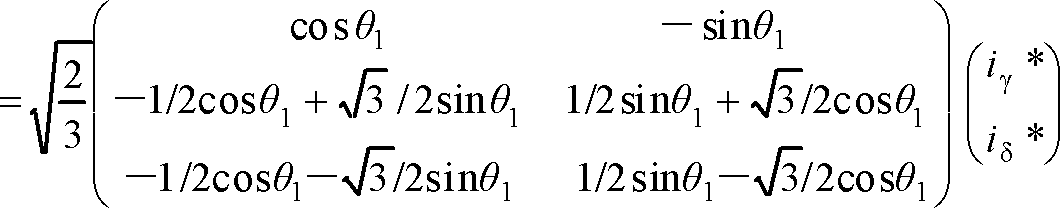 (2)
(2)
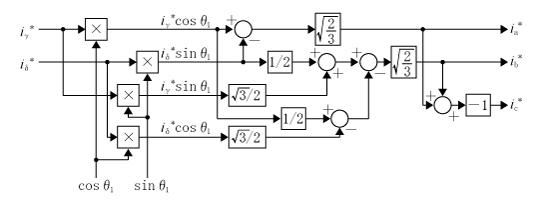
第2図にこの演算をブロック図で示す。
□内の記号または数値は演算法を示す。例として一番上のラインのia*についてみると、
になり、(2)式を再現している。ib*はやや複雑であるが、行列で示した演算を読み取ることができる。しかし、ic*の演算では行列の3行目を使う代わりに、三相電流の総和がゼロになる関係から式ic*=-(ia*+i b*)で単純計算している。
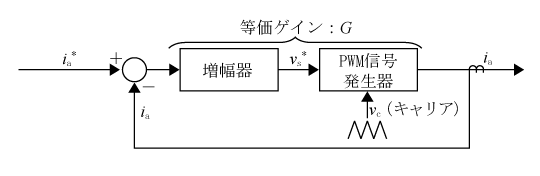
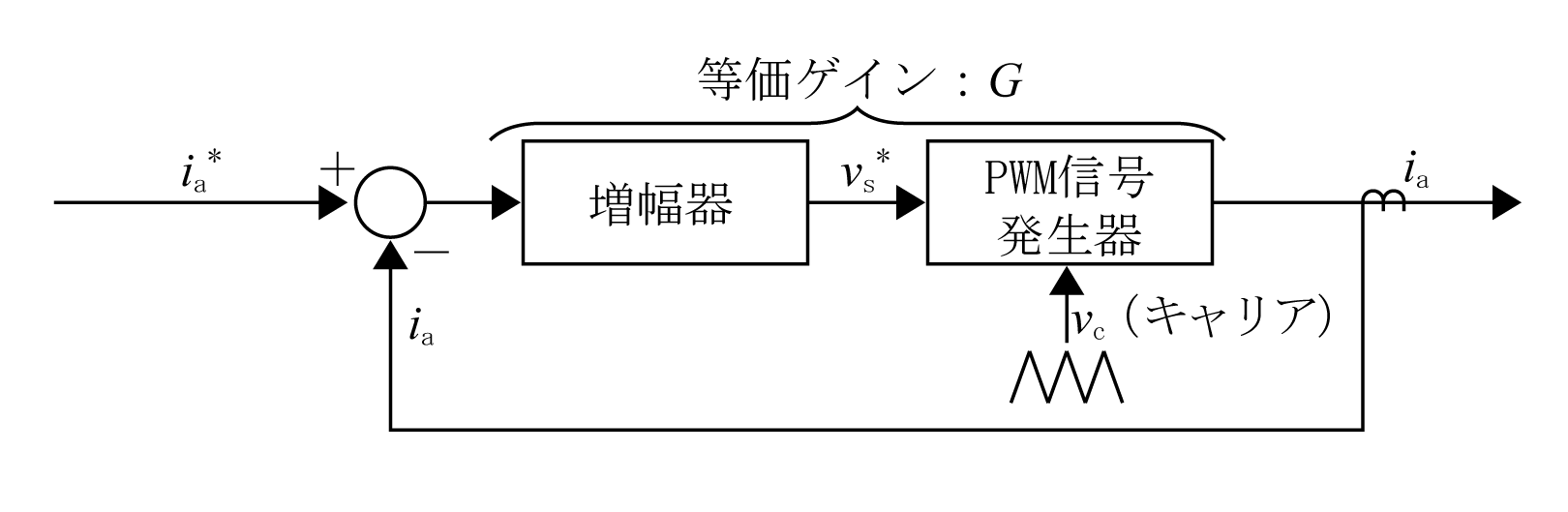
ここで、ia*、ib*、ic*が、ia、ib、icに等しくなることをia*とiaで説明しておく。該当部分のループ制御モデルを第3図に表現する。電流制御部及び電圧変換器の部分を等価的増幅度(ゲイン)Gとする。
このモデルで入力と出力の関係は(ia*-ia)×G=iaとなり、これをiaについて解くと、
となる。すなわち、電流制御部、インバータ、電流検出から成る電流フィードバックループは三相電流指令値ia*、ib*、ic*をインバータ出力電流ia、ib、icと比較し、その差が充分小さくなるように制御している。
この構成は磁束の位置(回転角θ1)を直接磁束センサから得ている。したがって、電動機の抵抗やインダクタンスなどの温度特性などによる変化の影響を受けないので制御が安定である。しかしその反面、特別に磁気センサを電動機内部に取り付ける必要があり、実用化に難がある。
(2)磁束検出によらないベクトル制御(間接型)
第4図は磁束検出器を用いずに、演算によりθ1を推量する磁気センサレスの磁束一定ベクトル制御の構成である。
この構成は先に「電動機ベクトル制御の基礎3 4.一次電流ベクトルの制御法」で説明した「滑り周波数形ベクトル制御」を実現したものである。
φ2一定の条件では指令値iγ、iδから次式より滑り周波数ωs*が求まる。
速度検出器を電動機回転軸に取り付けて回転角速度でωrを検出する。これにωsを加えてω1=ωr+ωsでω1が得られる。このω1を積分
![]()
![]() して回転磁束φ2の位置(角度)が求まり、cosθ、sinθ発生部で計算されて電流指令値演算部への入力となる。その後は、前節の磁気センサ付きベクトル制御に同じである。
して回転磁束φ2の位置(角度)が求まり、cosθ、sinθ発生部で計算されて電流指令値演算部への入力となる。その後は、前節の磁気センサ付きベクトル制御に同じである。
なお、点線部分は誘導機の速度を制御する場合に追加された部分である。検出された電動機角速度ωmとその指令値ωm*との差を速度制御器に入力して、トルク電流指令値を得るようにしてある。
この構成はやっかいな磁束検出器や磁束演算回路を必要としない反面、(5)式の電動機定数の変動、特に二次抵抗r2の影響を受けやすいという欠点がある。
(1)PM同期電動機の基本特性式
PM同期電動機(モータ)についてはこの講座シリーズの《機器材料-基礎・解説コース「PM同期モータについて」》で解説しているので、併せて参照されたい。
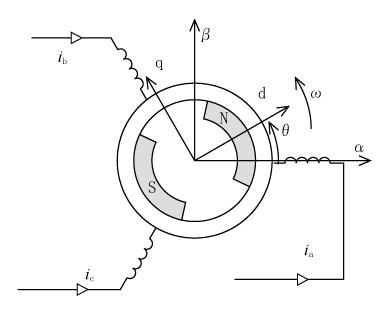
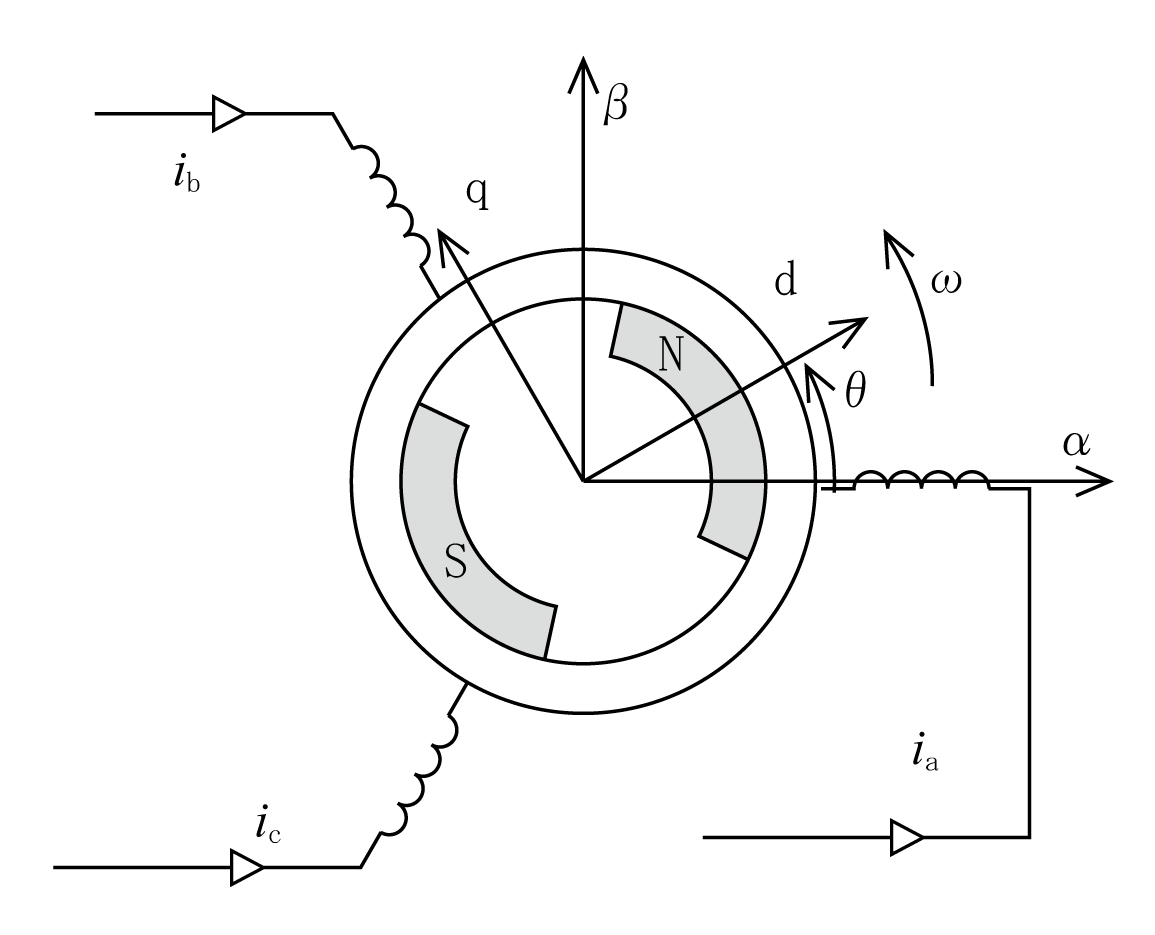
第5図にPM同期モータの解析用モデルを示す。固定子のU軸をα、β軸に合わせ、回転子の磁極に対応してd、q軸を設定した。なお、誘導電動機の場合と同様にしてva、vb、vc及びia、ib、icをU、V、W相の電圧及び電流とする。
PM同期モータの電流と電圧方程式は次式になる。
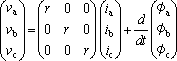 (6)
(6)
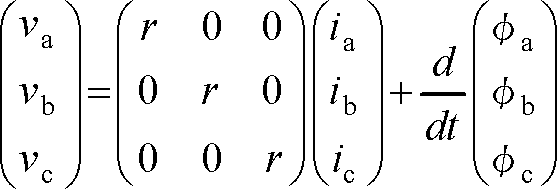 (6)
(6)
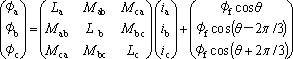 (7)
(7)
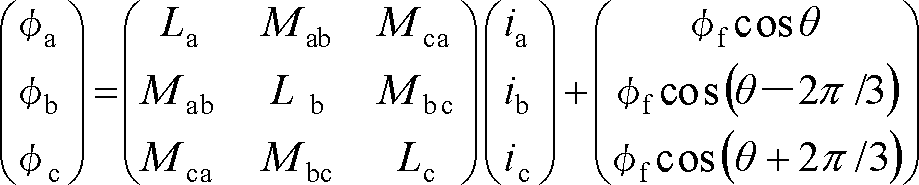 (7)
(7)
ただし、r:電機子巻線抵抗
φf:一相当りの永久磁石の電機子鎖交磁束
La、Lb、Lc:各相のインダクタンス
Mab、Mbc、Mca:相関の相互インダクタンス
(6)式は誘導電動機と同じであるが、(7)式では回転子の電機子鎖交磁束の項が加わる。ここでφfにかかるcosは各相への成分換算係数である。
また、インダクタンス群は誘導電動機の場合と違って、回転子と電機子との位置関係により各相で値が異なり複雑である。
(6)、(7)式を電圧と電流の式にまとめると、dθ/dt=ωとして、
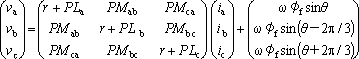 (8)
(8)
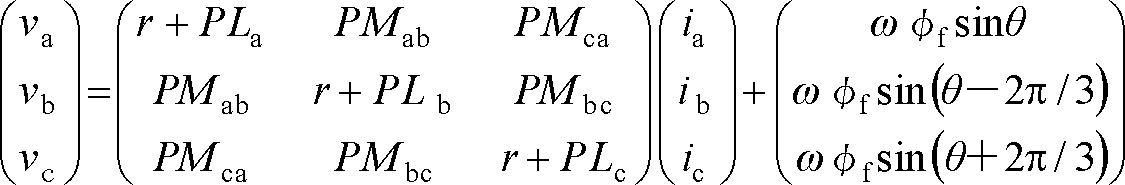 (8)
(8)
になる。
三相座標系の(8)式を二相のαβ座標系を経由して、電気角速度ωで回転し現在位置θのdq座標系に変換する。
であり、変換行列はθの回転方向は順方向なので以下になる。
この変換行列を用いて(3)式を変換すると、dq座標系の二相の電圧・電流方程式(11)になる。
ただし、vd、vq:電機子電圧のd、q軸成分
id、iq:電機子電流のd、q軸成分
Ld:d軸インダクタンス
Lq:q軸インダクタンス
第1項のLd、Lqは回転子の磁気回路により決定されるインダクタンスである。また、第2項は変換行列の計算から直接算出され、ωφaは永久磁石の電機子鎖交磁束による誘導電圧でq軸側だけに発生している。
(2)基本ベクトルとトルク制御
次にdq軸の電流が一定とみなせる定常状態でのPM同期モータの特性について調べる。定常状態では時間微分の演算子Pの項はゼロとなり(11)式の電圧・電流方程式は更に簡単化される。
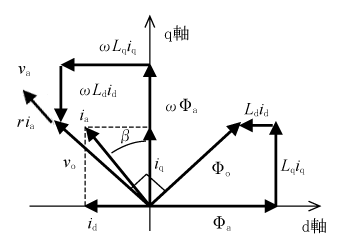
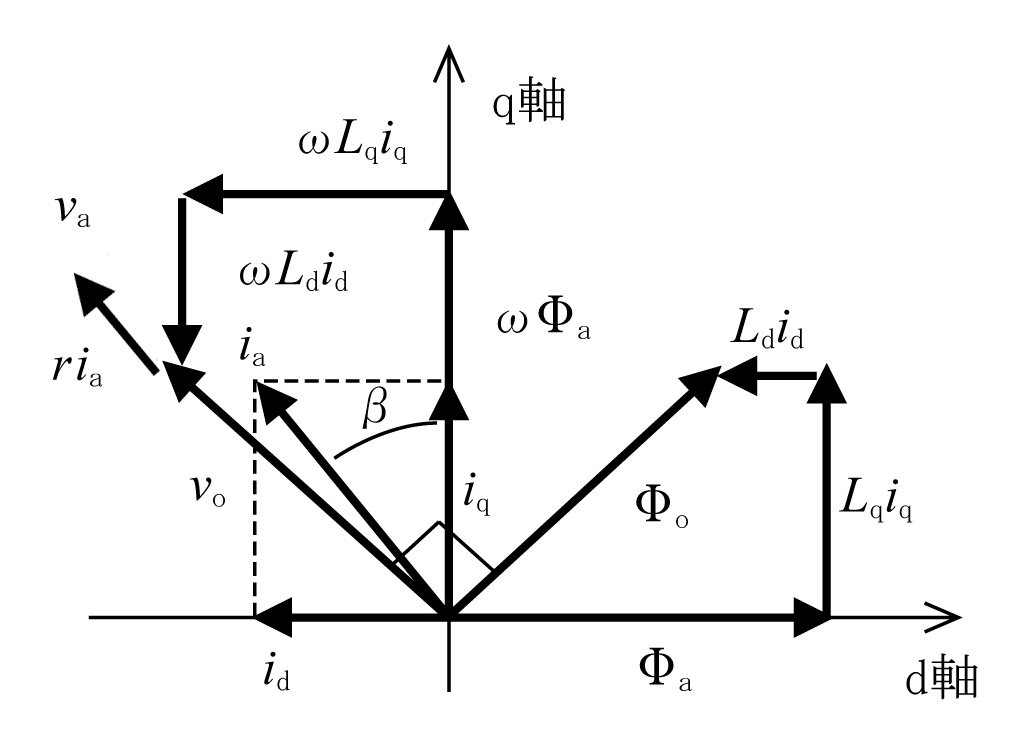
第6図の基本ベクトル図はこの式をベクトル図にしたものである。
dq座標を永久磁石の磁極の方向としたので、電機子鎖交磁束φaはd軸上にある。また、Ldid及びLqiqは各軸の鎖交磁束成分としてφaに加えられる。その結果、総合鎖交磁束のベクトルはφ0となる。入力電流iaは各軸の電流id、iqの合成であり、q軸との位相角がβとなる。この角度は無負荷時の誘導電圧(ωφa)を基準にした電流位相に相当する。端子電圧vaは誘導電圧に各軸の電機子反作用電圧ωLdid、ωLqiqを加えてvoとし、更に電機子巻線抵抗の電圧降下riaを加えたものになる。
基本ベクトル図から、極対数pの回転子に働くトルクは、電機子に働くトルクの反作用としてτ=-pia ×φoで計算できる。ベクトルの向きに注意してベクトル積を計算すると、
となり、更にid=ia sinβ、iq=ia cosβを使って表現すると、
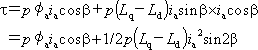 (14)
(14)
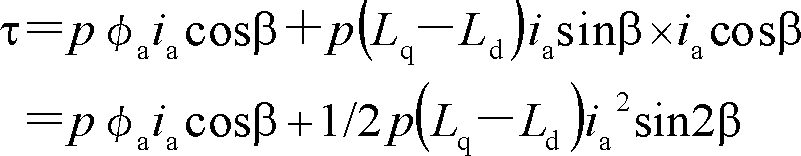 (14)
(14)
で、トルクは電流iaと位相角βで表現される。
電圧形インバータで駆動し電流フィードバック制御を行うと、電流ベクトル(d軸電流idとq軸電流iqまたは電流ベクトルiaと位相β)により、トルク特性を制御できることになる。電流ベクトル制御として、id=0制御、最大トルク制御、弱め磁束制御、力率1制御、最大効率制御などがある。
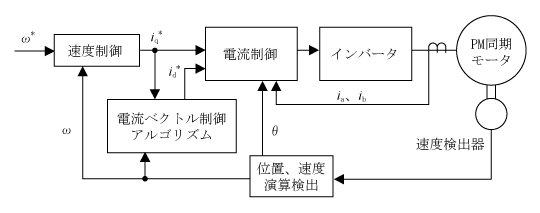
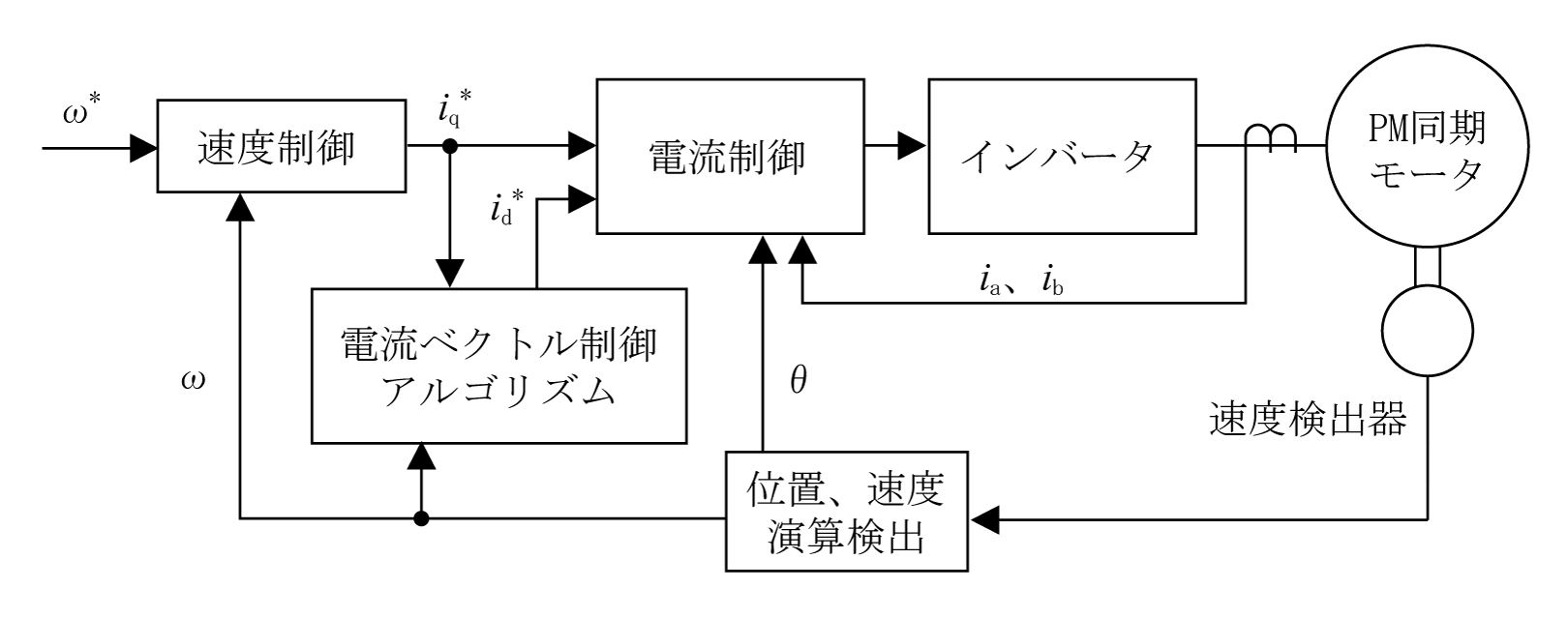
(3)電流ベクトル制御システム
第7図は電流制御を実現するシステムである。基本構成は先の「誘導電動機の磁束検出によらないベクトル制御」に同じで、それに電流制御アルゴリズムを演算する部分が付加されている。
まず、速度偏差を比例・積分制御などで誤差増幅してq軸電流指令iq*を作成する。q軸電流指令iq*と必要であればモータ速度を「電流ベクトル制御アルゴリズム」へ入力する。そこでは制御目的に合わせたアルゴリズムの演算でd軸電流指令id*を求める。そして、第4図の誘導機に同等な方式でid*、iq*を三相変換しインバータを通して、PM同期モータを駆動する。
これにより選択されたid =0制御や最大トルク制御などの「電流ベクトル制御アルゴリズム」に沿ったPM同期モータの動きになる。
以上で「電動機ベクトル制御の基礎」の解説を終える。更に詳しくは巻末の参考文献や新刊の技術文書を参照されたい。多少難解な部分もあるが、これまでの説明した知識でもって相応の理解が可能と思う。
(1) インバータドライブハンドブック編集委員会編:インバータドライブハンドブック、日刊工業新聞社刊
(2) 片岡昭雄:電動機の可変速駆動入門、森北出版株式会社刊
(3) 赤木泰文:ACモータのベクトル制御、電学論D 108巻8号 1988
(4) 武田洋次、松井信行、森本茂雄、本田幸夫共著:埋込磁石同期モータの設計と制御、オーム社刊
(5) 株式会社日立製作所総合教育センタ技術研修所編:わかりやすい小型モータの技術、オーム社刊
(6) 竹下隆晴、野村尚史、松井信行:電流推定誤差に基づくセンサレスブラシレスDCモータ制御、電学論D 115巻4号、1995