〜終わり〜
■ぜひアンケートにご協力下さい■


テブナンの定理を利用する計算は、
① 回路の一部を切断して切り口を作り、そこに現れた電圧Eとそこから電源側をみたインピーダンスZからなる等価回路を作る。
② 電源側の等価回路に残りの回路を接続して電流と電圧を求める。
という順序で行う。
例題では第2図のように地絡箇所の直前で回路を切断する。切断によって地絡していた回路は正常に戻り、線路のインピーダンスを無視したので切断点には相電圧が現れる。
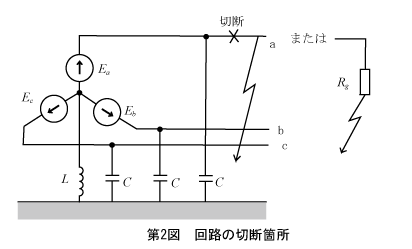
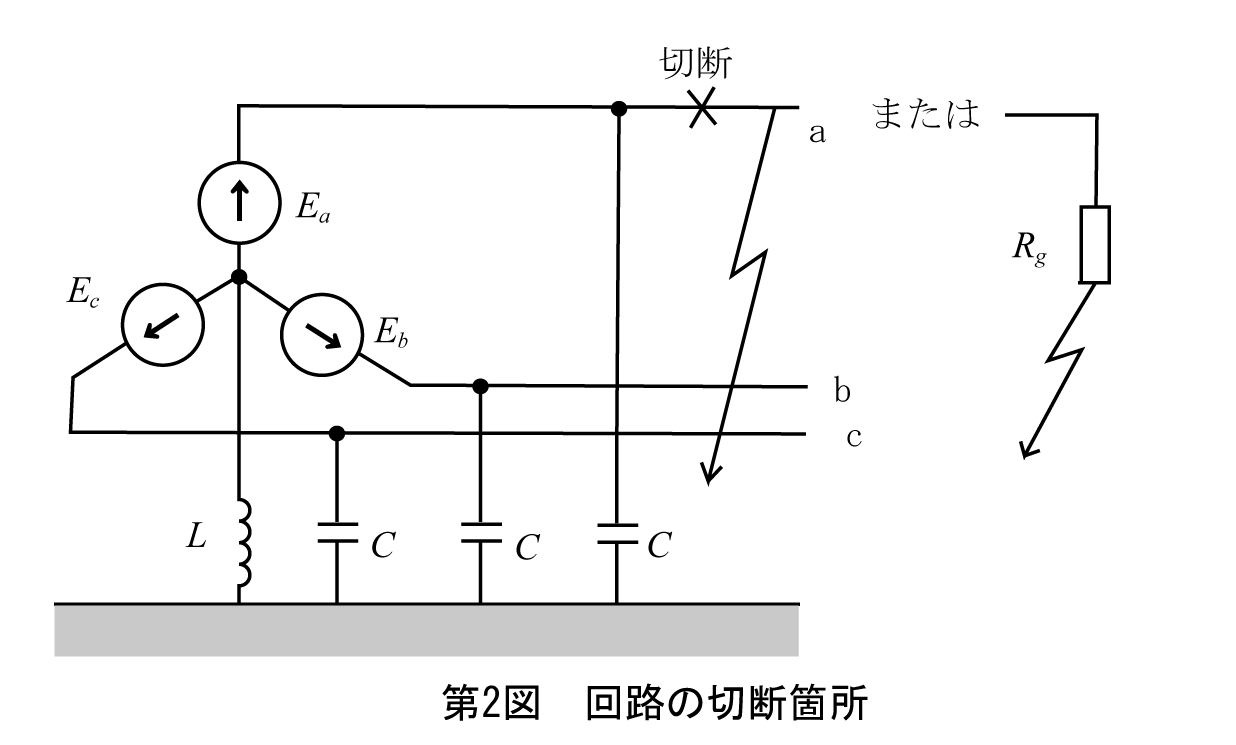
電源側をみたインピーダンスは、定電圧電源を短絡し定電流源は開放した回路で求まる。この例では定電圧電源なので、それを短絡して第3図の回路になる。
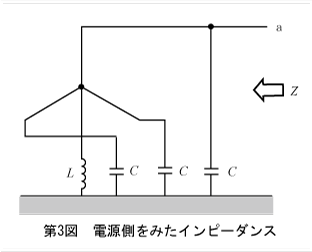
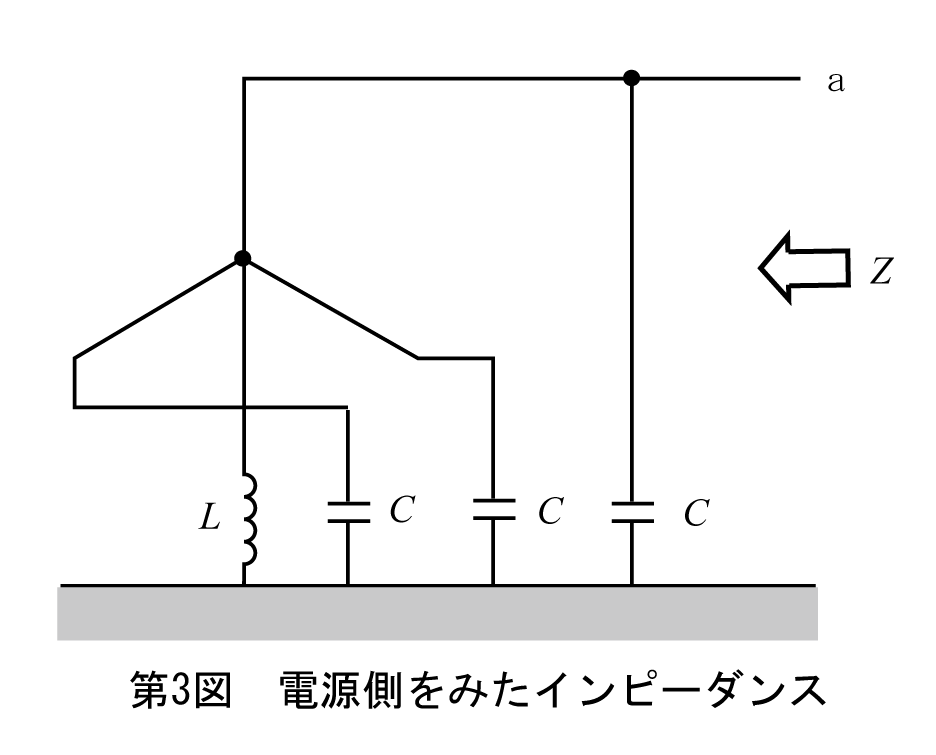
図から容易に、
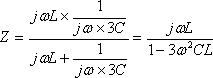 (1)
(1)
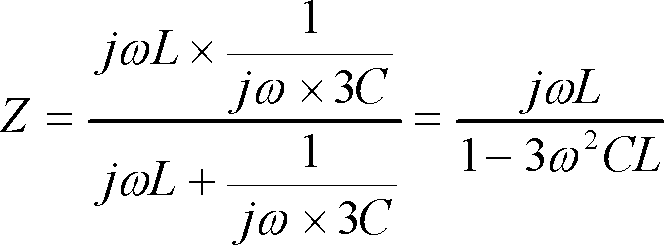 (1)
(1)
を得てテブナンの定理での等価回路が第4図のように完成する。
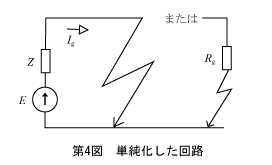
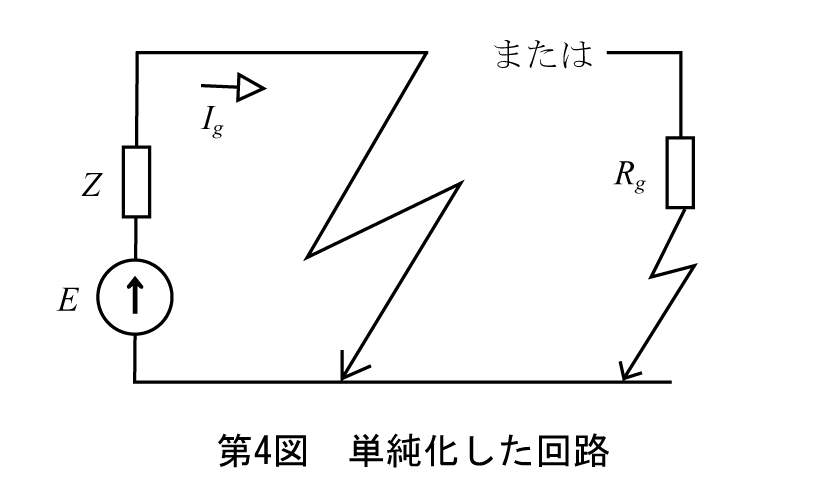
準備ができたので第4図から地絡電流を求める。完全地絡の電流Igは、
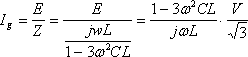 (2)
(2)
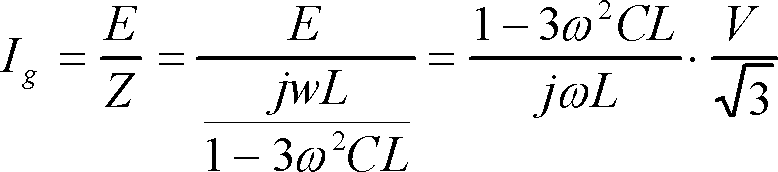 (2)
(2)
となる。また、地絡が抵抗値Rgをもつ不完全地絡のでは、
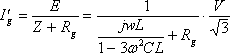 (3)
(3)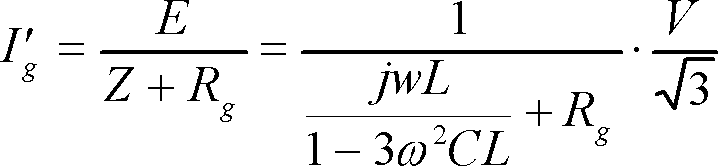 (3)
(3)
と計算される。
回路が並列で接続されている場合に威力を発揮する定理である。
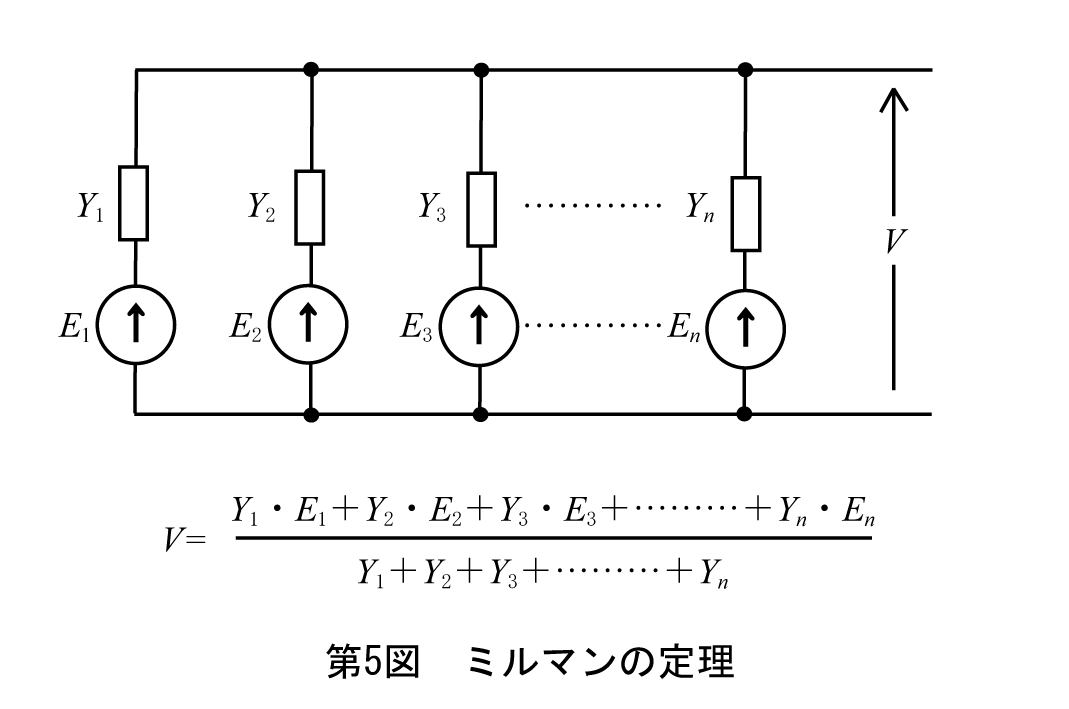
第5図にミルマンの定理を示す。回路を電源とアドミタンスからなる枝の並列接続に変形する。枝の両端の電圧Vは各枝のアドミタンスの和を分母とし、電源とアドミタンスの積の和を分子とした式で計算される。
三相電源の回路はミルマンの定理からみると3個の並列回路(中性点接地では4個の並列回路)となるので非常に都合がよい。また、ほとんどの三相回路計算では中性点の電位が分かれば、あとは各相ごとの単相回路の計算に単純化される。
ミルマンの定理の活用手順は次のようになる。
① 中性点電圧を最初に求める。
② 中性点電圧との差電圧と線間のインピーダンスより線電流を計算する。
早速、例題に適用してみよう。第6図に完全地絡の回路をミルマンの定理向けに変形する。
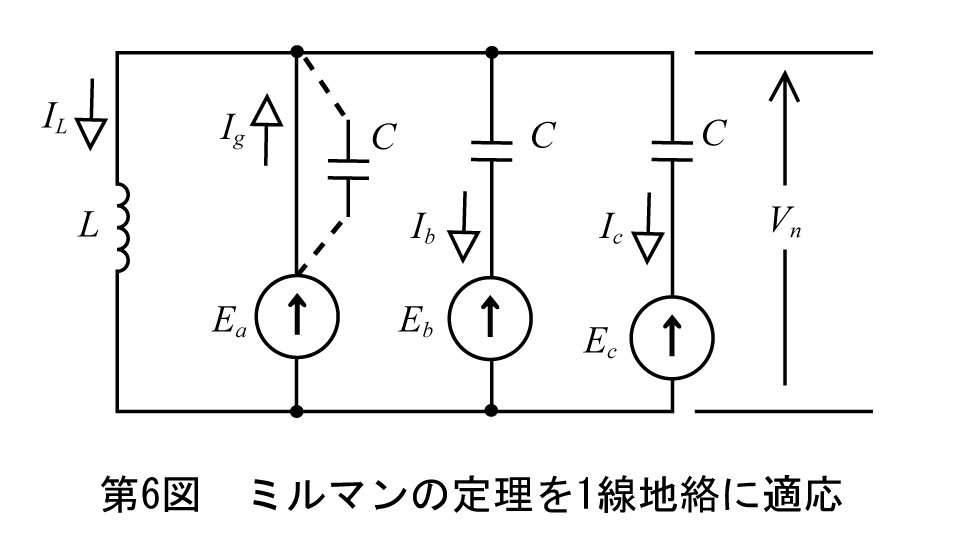
不幸(?)にして完全1線地絡ではミルマンの定理を使う間でもなく中性点とGNDの間の電圧はEa(=E)であることが分かり、最初の電圧計算の ① は省略される。後は回路に沿ってIgを計算すれば、
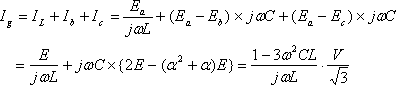 (4)
(4)
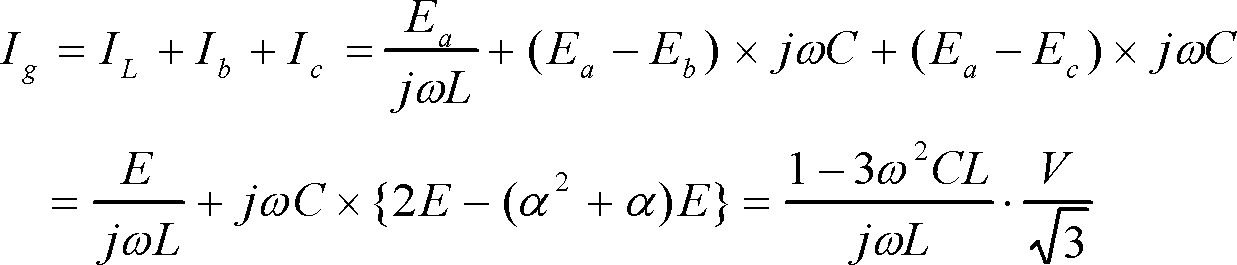 (4)
(4)
が得られる。
ここで、
![]()
![]()
であり、Ea=E,Eb=α2E,Ec=αEと1+α+α2=0の関係を利用した。
次に地絡抵抗がRgの場合を考える。並列回路に変形した地絡の回路は第7図のようになる。
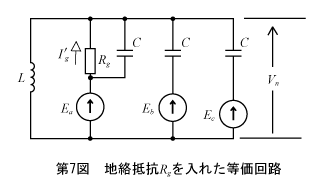
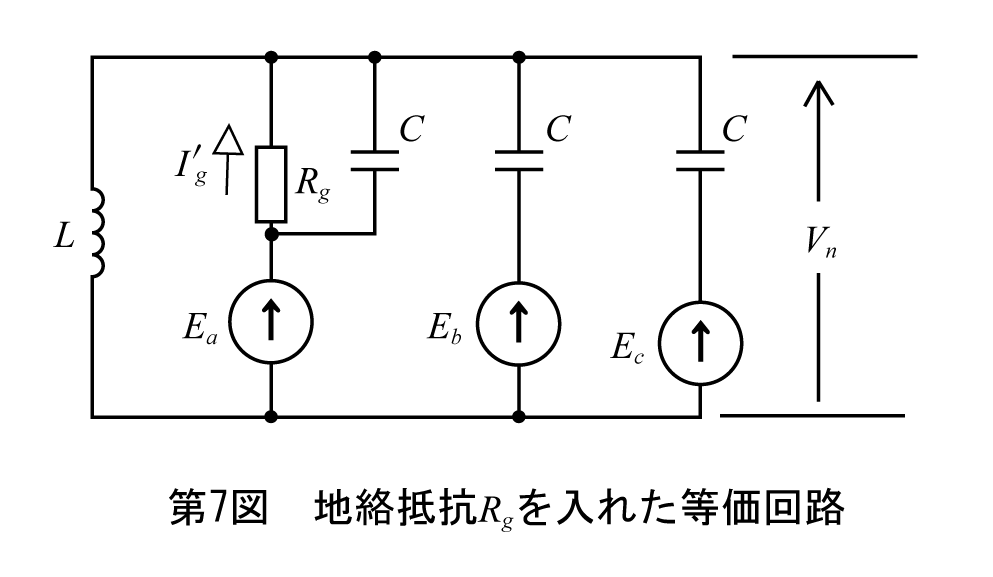
手順に沿ってまず ① の中性点電圧Vnを求める。ミルマンの定理の式によって
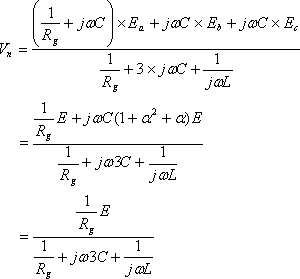 (5)
(5)
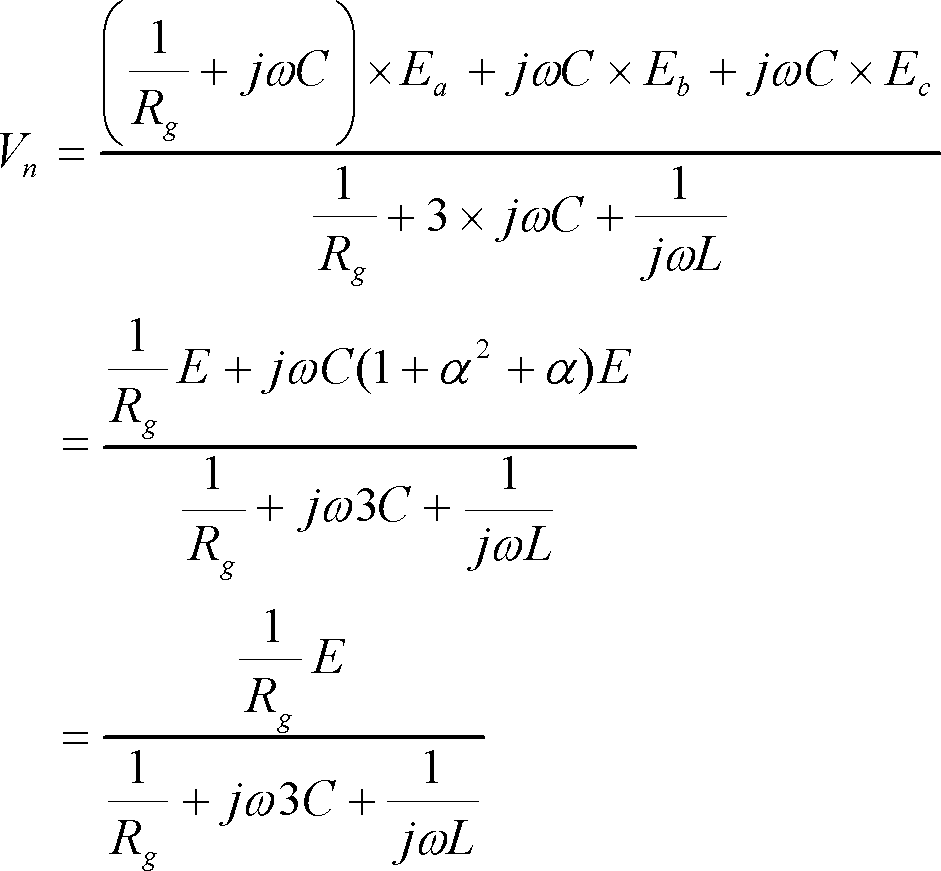 (5)
(5)
ここで、消弧コイルの枝には電源がないので、分子にLが出てこないことに注意してほしい。また、ここでも1+α+α2=0の関係を利用している。
地絡電流Ig’はRgを流れる電流なので、Vnとa相の相電圧Eとの差をRgで割ればよい。すなわち、
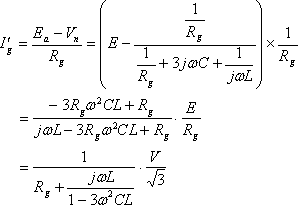 (6)
(6)
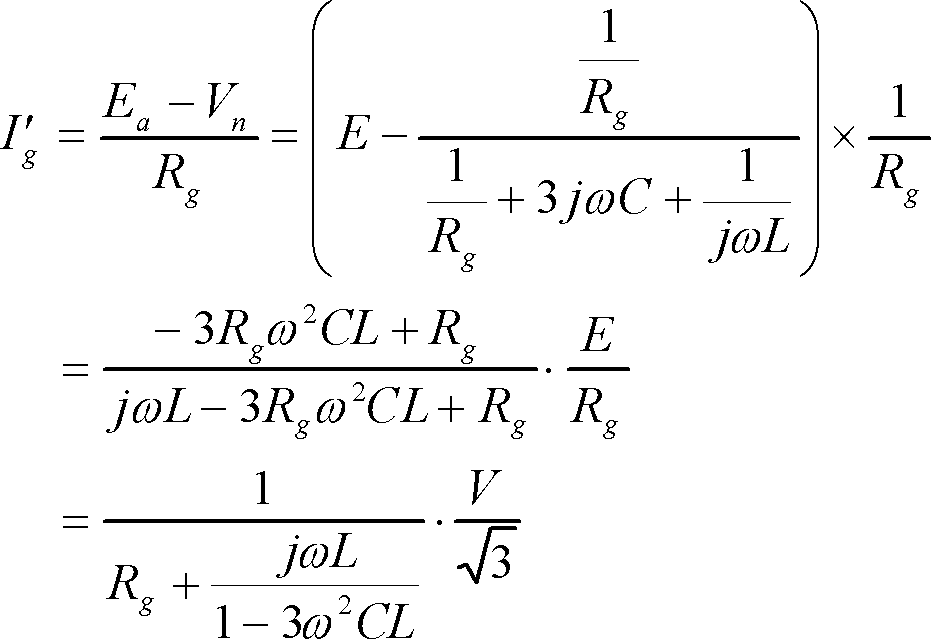 (6)
(6)
と計算される。
故障電流を零相、正相、逆相に分解して解いていく方法で三相回路の計算に出てくる最もポピュラーな計算手法である。
三相平衡電源として、相電圧E、各相の電流をIa、Ib、Icまた零、正、逆相の電圧、電流、インピーダンスをおのおのI0、I1、I2、V0、V1、V2、Z0、Z1、Z2とする。
電圧と電流の関係は三相平衡電源の場合E0=E2=0、E1=Eを考慮して、
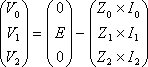 (7)
(7)
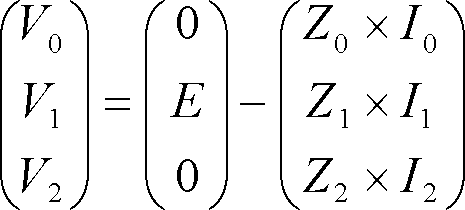 (7)
(7)
であり、相電流については、
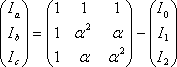 (8)
(8)
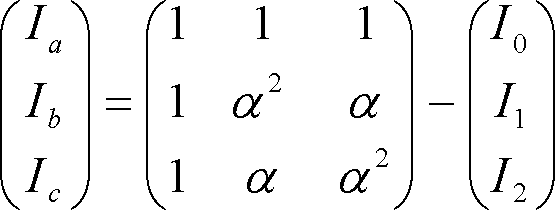 (8)
(8)
である。または、I0、I1、I2について解いた次の式にすることもある。
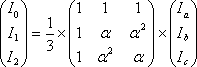 (9)
(9)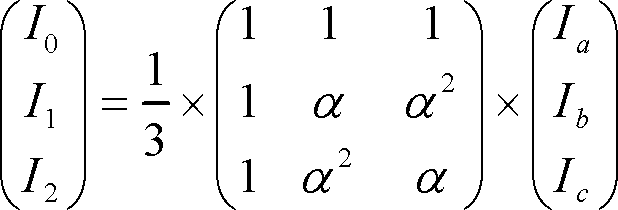 (9)
(9)
この基本式に1線地絡の条件を代入していく。
a相1線地絡の条件 Ia=Ig、Ib=Ic=0、Va=0 から、電流の式は次のようになる。
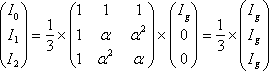 (10)
(10)
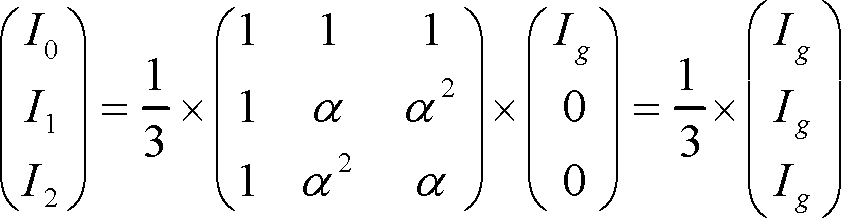 (10)
(10)
I0=I1=I2=1/3×Ig=1/3×Iaである。
電源側については零相、正相、逆相のインピーダンスをZ0、Z1、Z2として電圧の基本式に代入すると、
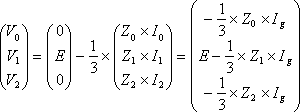 (11)
(11)
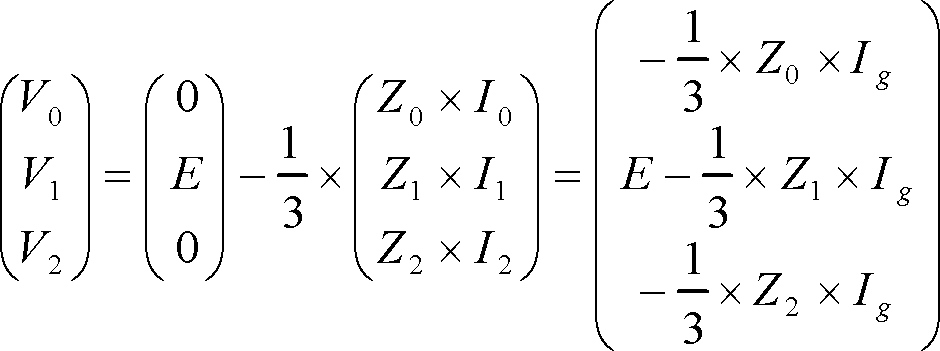 (11)
(11)
になる。
冷静に対処しないと、ここらへんで混乱してしまうのがこの方法の欠点である。電源側の条件と負荷側の条件をはっきりと区別しておくことがポイントである。
負荷側の条件、すなわちa相の地絡条件 Va=V0+V1+V2=0 の関係に代入して、
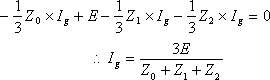 (12)
(13)
(12)
(13)
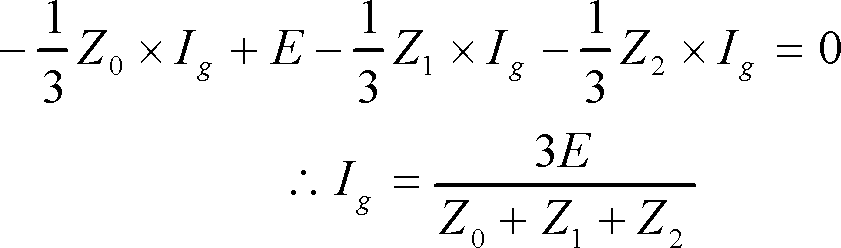 (12)
(13)
(12)
(13)
となり地絡電流Igが求まる。
ここでZ0、Z1、Z2の値を求める。Z0は対地間に流れる電流に関与するインピーダンスなので第8図で考える。
定電圧を短絡した回路を作り、消弧リアクトルを3個に等価分解して1相分の回路を作る。
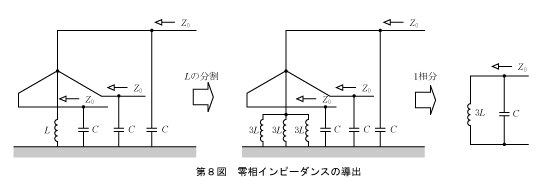
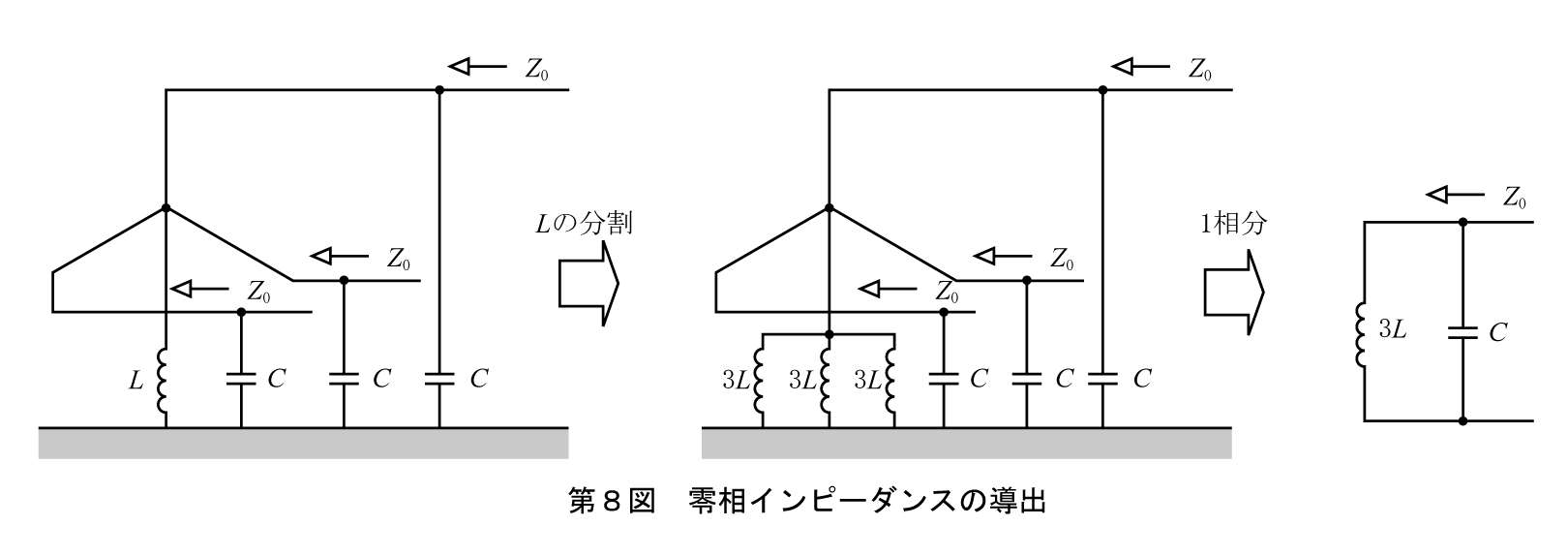
等価回路からZ0が次式となる。
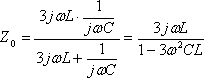 (14)
(14)
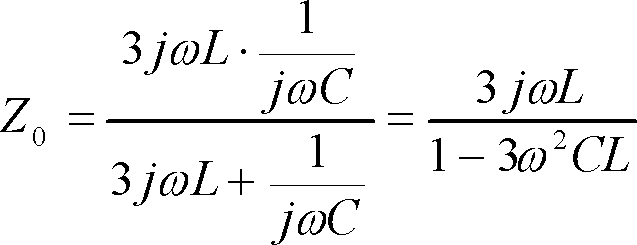 (14)
(14)
Z1、Z2はE1、E2に直列に入るインピーダンスで、送電線上に存在する抵抗やインダクタンスである。例題ではこれらを無視しているので Z1=Z2=0 である。
以上をまとめると、
が得られる。
次にVaに注力する。Va=V0+V1+V2であり、Rgを通しての地絡条件から Va=Ig’×Rg である。これらの関係から以下の方程式が得られる。
Ig’について解くと
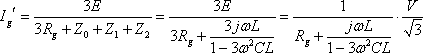 (17)
(17)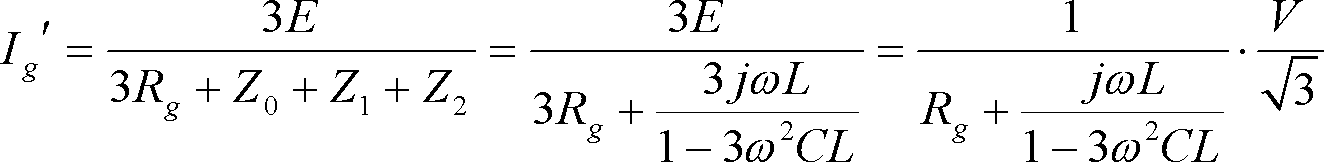
であり、前出の各定理による結果と同じ式が得られる。
実際に問題にぶつかったときはどの方法で解いてもよいが、皆さんはどの方法がお気に入りであろうか。筆者はミルマンの定理派である。ミルマンの定理は回路を並列形に変形するだけで特別な細工が不要なので、ミスを犯す危険性が低いのが理由である。
ただ、ご覧のように代数的に多少ゴタゴタしてしまう。でも1+α+α2=0の形が出てくるので最終的にすっきりする。
対称座標法は相のインピーダンスや式が多くでてきてややこしくなるきらいがある。テブナンの定理は定理の活用点(切断する部分)の選定がポイントである。ここが旨味の出る所かもしれないが、試験場では旨味など出す余裕がないのが実状ではなかろうか。その点ミルマンの定理は三相電源の中性点電位を簡単につかみ取れるからあとの処理が容易である。使ってみると非常に便利な定理である。
第9図は三相2回線(A,B回線)でA回線からB回線の1線への静電誘導電圧E0を求める問題である。
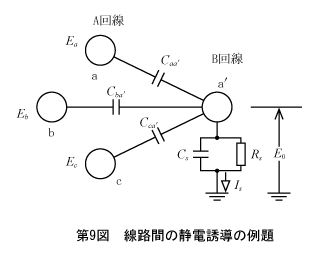
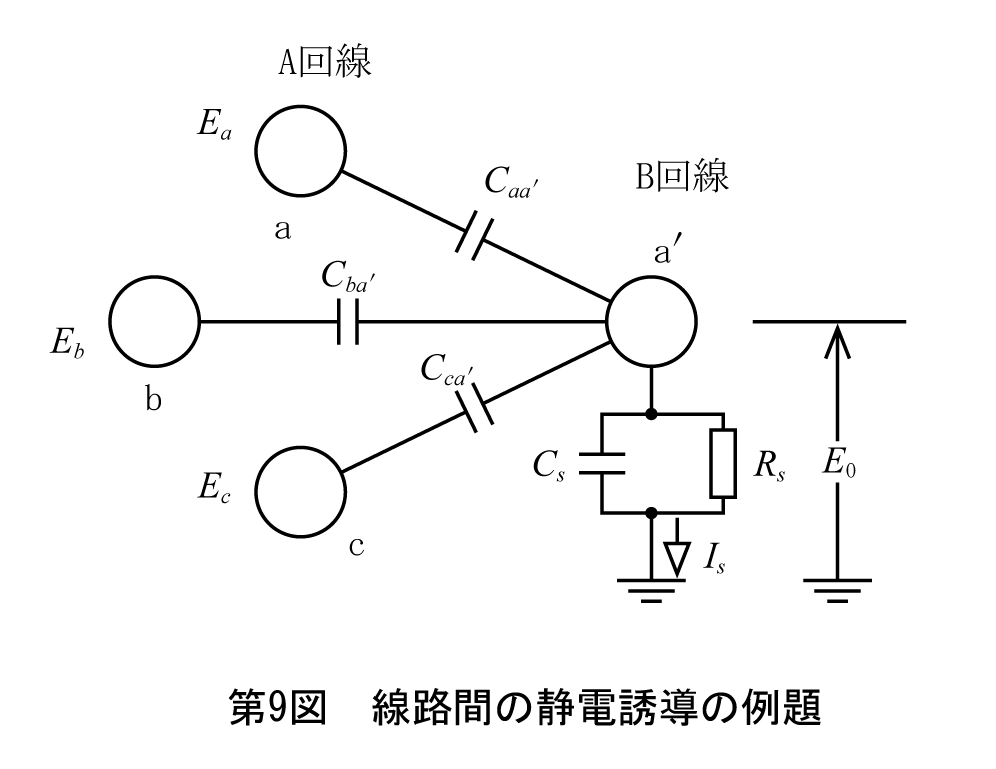
ミルマンの定理を使えば一発で、
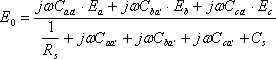 (18)
(18)
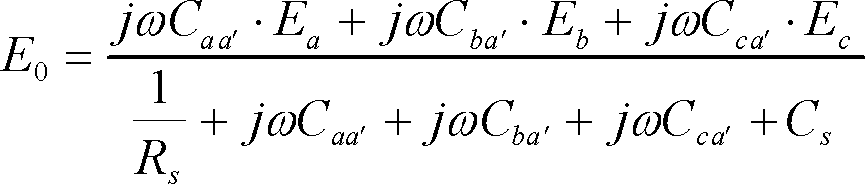 (18)
(18)
が出てしまう。
ただ、一つの解法にこだわる必要はない。ケースバイケースで各解法を駆使して三相回路の苦手意識を克服してもらいたい。
