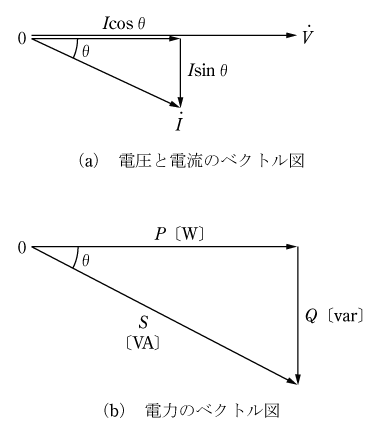
直流は電圧と電流が同方向で一定であるが、交流の電圧と電流の関係はベクトル図で示すと電圧を基準にして電流はθ遅れの第1図（a）のようになる。ここで、電圧、電流には実効値V、Iを用いる。

　図から電圧と同相の電流I cosθは有効電流、90°位相が異なるI sinθは無効電流である。

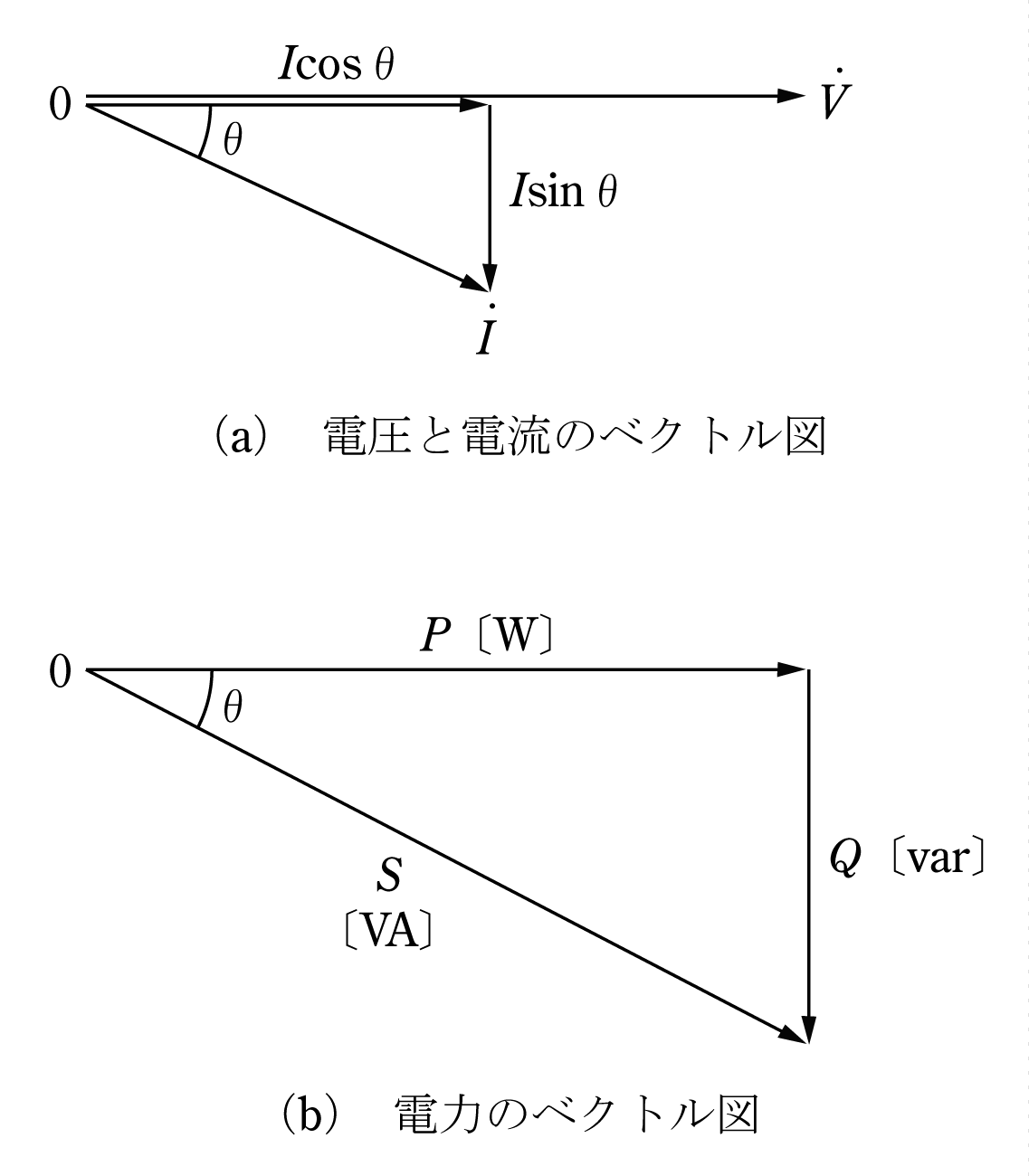
　両者の積の電力を第1図（b）に示す。

　電圧と同方向のP=VI cosθを有効電力〔W〕、90°位相が異なるQ=VI sinθを無効電力〔var〕、電流と同方向のS=VIを皮相電力〔VA〕という。3者の関係は（1）式である。

　　P=S cosθ　　　 Q=S sinθ　　　 （1）

　ここでcosθを力率という。

　問題の解答にあたっては第1図（b）が重要である。

■第1図■

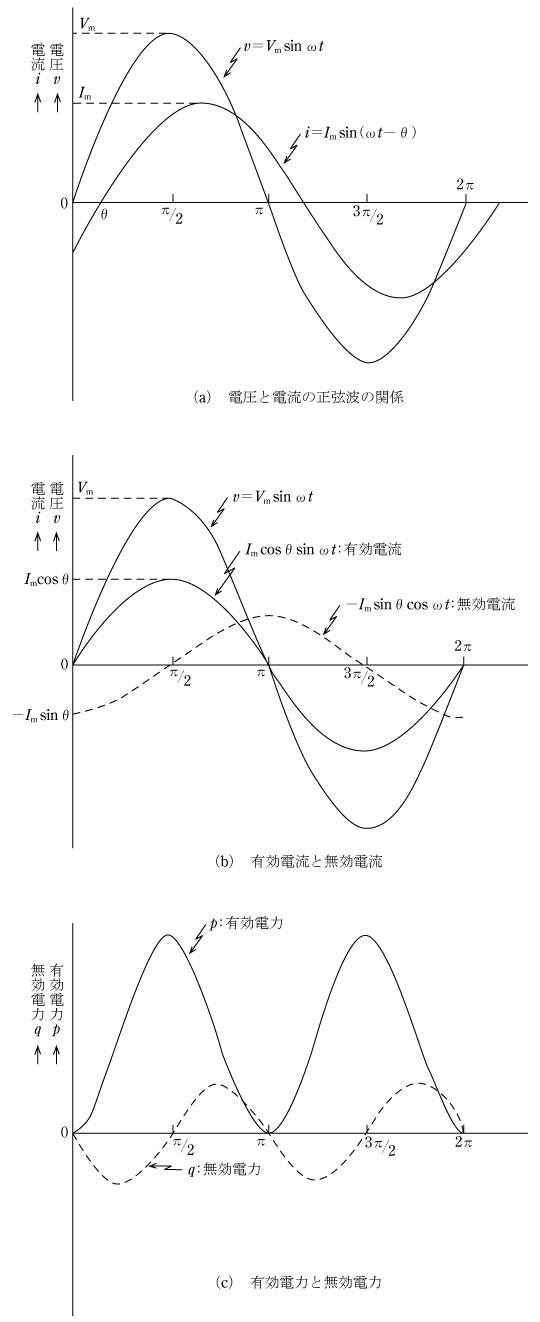
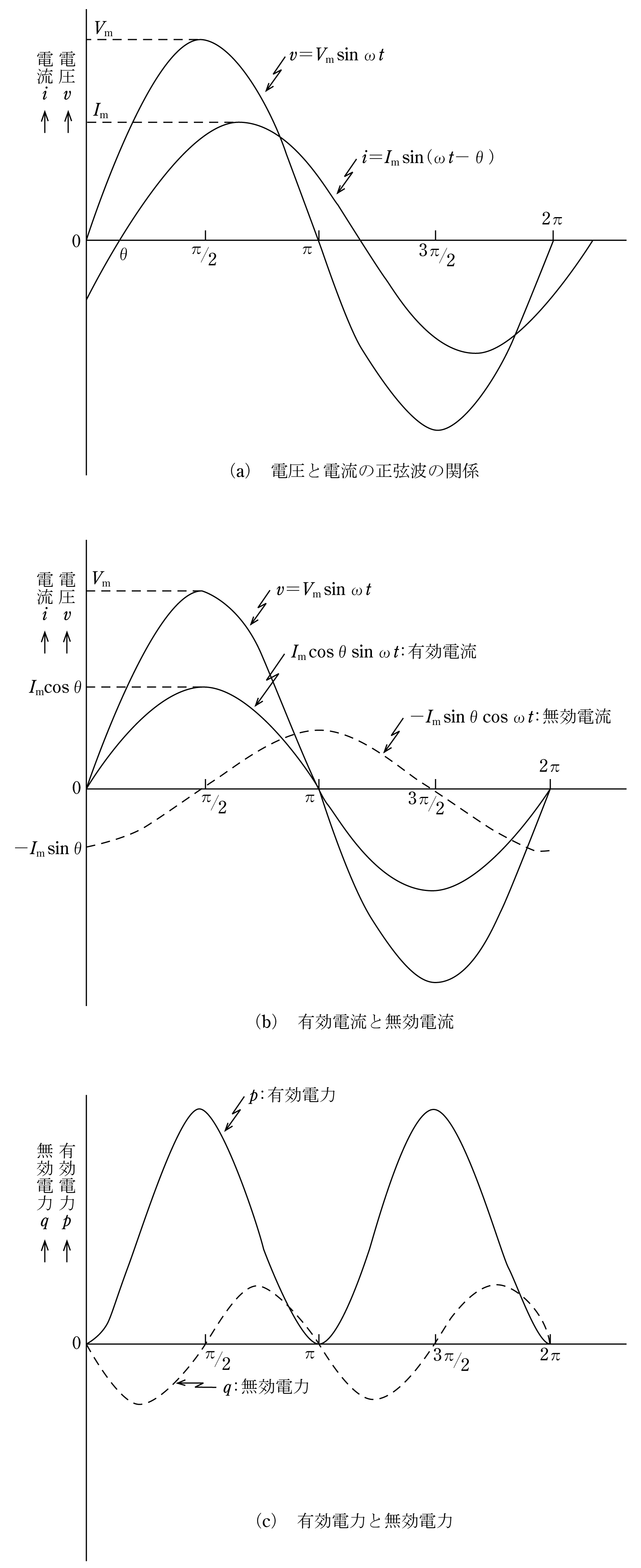
　次に電圧と電流の関係を瞬時の正弦波で表すと第2図（a）となり、最大値をV_m、I_mとして、電圧v=V_msinωtで電流がθ〔rad〕遅れとすると、電流iは（2）式となる。

　i=I_msin（ωt－θ）=I_m (sinωt cosθ－cosωt sinθ）

　　　　　　　　　　　　=I_m cosθsinωt－I_m sinθcosωt

　　　　　　　　　　　　=I_m cosθsinωt＋I_m sinθsin(ωt－π/2) （2）

　（2）式をグラフにすると第2図（b）となる。図からI_m cosθsinωt は電圧と同相の波形で有効電流、I_m sinθsin(ωt－π/2)は電圧より90°遅れの波形で無効電流という。次に電圧×電流は両者が同相の場合は有効電力pで(3)式となり第2図（c）のように常にプラスである。

　p=V_msinωt×I_m cosθsinωt=V_mI_m cosθsin²ωt= （3）

　90°位相が異なる場合は無効電力qで（4）式となり、第2図（c）のようにプラスとマイナスを繰り返す。

　q=V_msinωt×(－I_m sinθcosωt)

　　=－V_mI_m sinθ(sinωt cosωt)=－V_mI_m sinθ （4）

　この無効電力は仕事ではないので無効電流を0にして有効電流だけにすること、すなわち力率cosθを1にすることが最も効率的となる。

■第2図■

　試験問題をベースに力率改善の方法、負荷増設に伴う設備容量の確保策、力率改善と損失軽減について解説する。

（1）力率改善

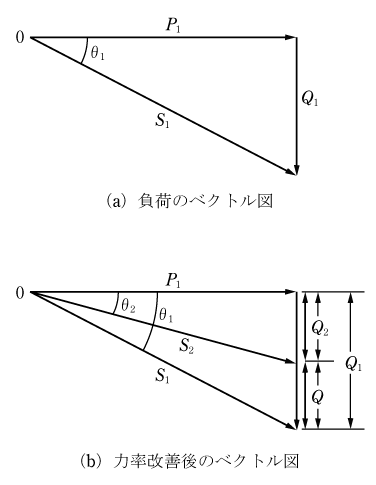
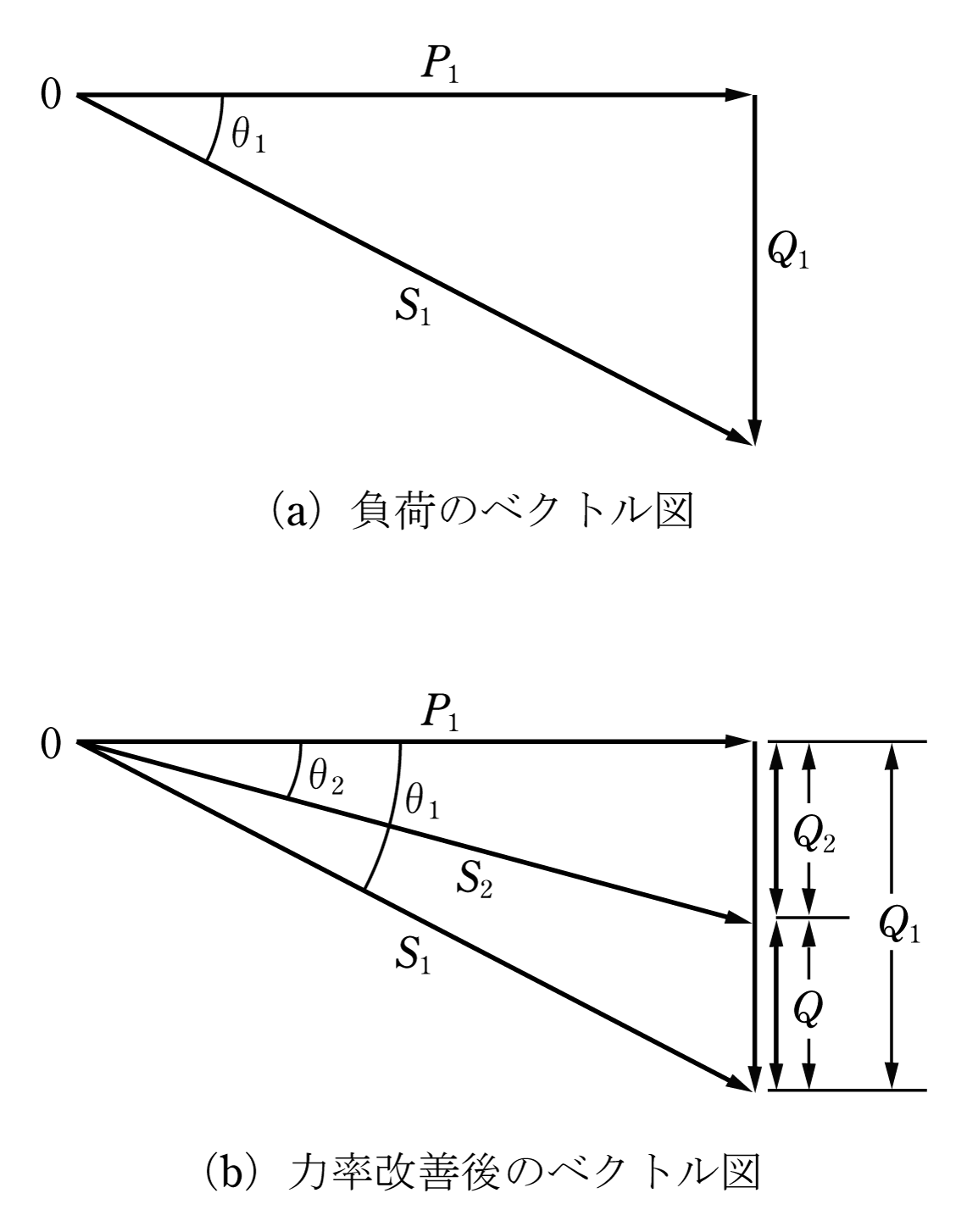
　遅れ力率の負荷の力率を改善するには、負荷と並列にコンデンサを接続し進み電流を流して無効電流を減少させる。具体的には有効電力P₁〔W〕、遅れ力率cosθ₁とすると、無効電力Q₁〔var〕、皮相電力S₁〔VA〕を示すベクトル図は第3図（a）となる。図からS₁、Q₁は（1）式を用いて（5）式のように計算する。

　 S₁ = P₁/cosθ₁

　 Q₁= = (P₁/cosθ₁ )sinθ₁= P₁ /cosθ₁（5）

　次に力率改善のために容量Q〔var〕の電力用コンデンサを負荷と並列に接続すると、進相無効電力Qとして作用するので、第3図（b）のベクトル図のように、力率改善後の有効電力P₁〔W〕は一定で、無効電力Q₂〔var〕、皮相電力S₂〔VA〕、力率cosθ₂は次の（6）式となる。

　 Q₂= Q₁―Q　　　　S₂= 　cosθ₂= P₁ / S₂（6）

　第3図（b）のベクトル図が極めて重要である。

■第3図■

（2）負荷増設と設備容量の確保策

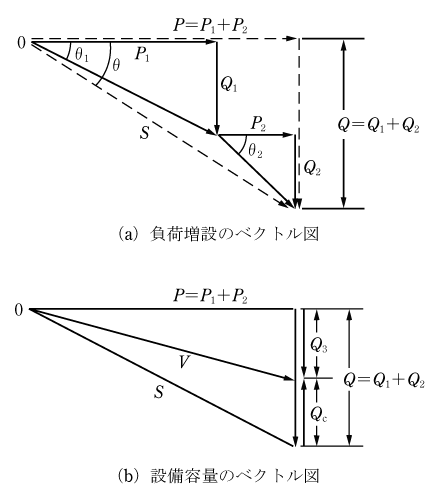
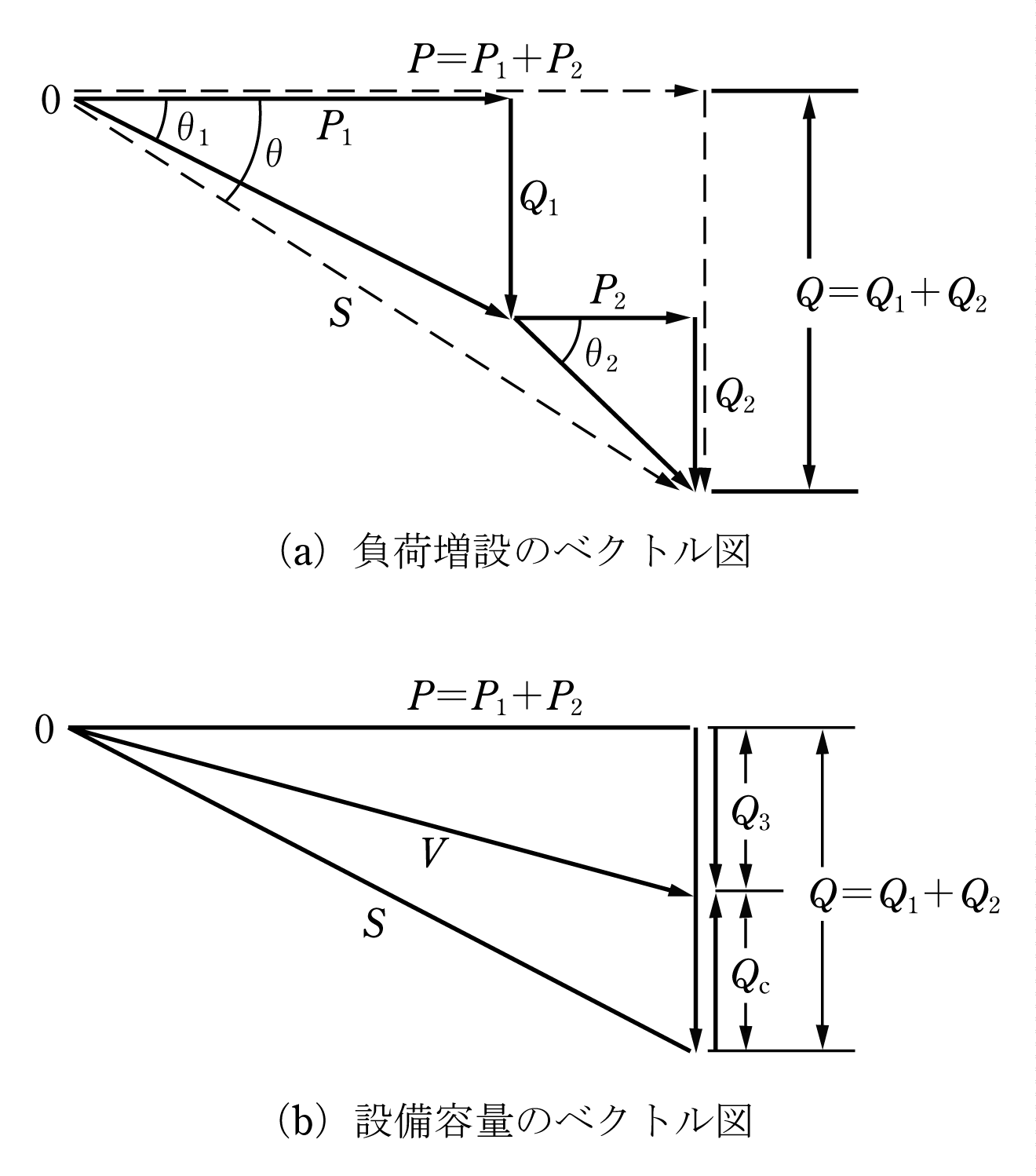
　有効電力P₁、力率cosθ₁の負荷がある。これに有効電力P₂、力率cosθ₂の負荷を増設した場合、合成された有効電力P、無効電力Q、皮相電力S、力率cosθは第4図（a）のベクトル図を用いて（7）式となる。

　 P=P₁+ P₂　　　Q=Q₁+Q₂=(P₁/ cosθ₁ )sinθ₁+ (P₂/ cosθ₂ )sinθ₂

　 S= 　　　cosθ = P / S（7）

　次に、第4図（b）のベクトル図のように負荷の増設により皮相電力S〔VA〕が供給設備である変圧器の設備容量V〔VA〕より大きい場合、変圧器は容量オーバーの過負荷となる。ここで皮相電力を減少させるために、負荷にコンデンサを並列接続して無効電力を減少させS=Vとすることができる。これによって負荷の増設の場合も有効電力が変圧器の設備容量を超えない限りコンデンサを設置することで皮相電力を変圧器の設備容量以下にすることができる。具体的な計算方法は第4図（b）のベクトル図から、

　・皮相電力Vの場合の無効電力Q₃= 〔var〕（8）

　・必要なコンデンサの容量Q_c=( Q₁+Q₂)－Q₃〔var〕（9）

　ここで大切なことは第4図（a）のように負荷を合成するベクトル図を作ること、設備容量は皮相電力と同様の扱いをすることである。

■第4図■

（3）力率改善と損失軽減

　有効電力Pは一定で線路の抵抗r〔Ω〕、負荷側の電圧V〔V〕、負荷電流I₁〔A〕、力率cosθ₁とすると、線路損失p₁は電流の2乗に比例する（10）式となる。

　　　　p₁ =r(I₁)²（10）

　コンデンサを導入して負荷電流I₂〔A〕、力率cosθ₂とすると、線路損失p₂は（11）式のようになる。

　　　　p₂ =r(I₂)²（11）

　力率改善による前後の線路損失の関係p₂/p₁は（12）式となるので、皮相電力に対しては2乗に比例し、力率に対しては2乗に反比例することになる。

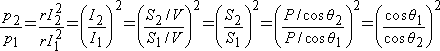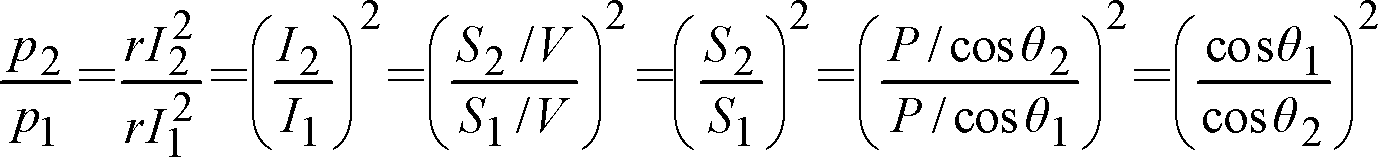（12）

（12）

　次にコンデンサ設置による力率改善で損失がX〔％〕減少した場合のコンデンサの容量Q〔var〕の計算について解説する。

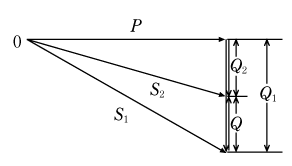
　 損失がX〔％〕減少した場合のp₁とp₂の関係はp₂= p₁×(100－X/100)となる。この関係を用いて、第5図のように有効電力Pは一定でコンデンサ設置前の皮相電力S₁、無効電力Q₁、コンデンサQ設置後の皮相電力S₂、無効電力Q₂とすると（12）式からS₂は（13）式となる。

VA〕(13)

VA〕(13)

　Q₂は となるので、設置されたコンデンサの容量Qは（14）式になる。

〔var〕（14）

〔var〕（14）

■第5図　損失軽減時のベクトル図■

　ここでは（12）、（13）、（14）式と第5図のベクトル図が重要である。

　過去の問題は以下のとおりで、ポイントを解説する。

（1）力率改善の計算

　10,000kVA、遅れ力率80％の負荷に電力を供給している変電所がある。負荷と並列に2,000kvarのコンデンサを設置した場合、次の（a）及び（b）に答えよ。

　（a）コンデンサ設置後の無効電力〔kvar〕の値として、正しいのは次のうちどれか。

　　（1） 1,000　（2） 2,000　（3） 3,000　（4） 4,000　（5） 5,000

　（b）変圧器にかかる負荷の力率〔％〕の値として、正しいのは次のうちどれか。

　　（1） 86.6　（2） 89.4　（3） 93.0　（4） 95.2　（5） 97.5

（a）の解答

　コンデンサ設置前の無効電力Q₁は（5）式にS₁=10,000、P₁=10,000×0.8=8,000を入れて、

　コンデンサ設置後の無効電力Q₂は（6）式から、

　　　Q₂₌Q₁―Q=6,000－2,000=4,000〔kvar〕

　〔答〕　(4)

（b）の解答

　第3図（b）を利用して（6）式から皮相電力S₂は、

　　　S₂= 〔kVA〕

　設置後の負荷の力率cosθ₂は、

　 cosθ₂=P₁ / S₂=8,000/ = =0.894

　〔答〕　

　(2)

（2）負荷増設と設備容量の確保策

　定格容量500kVAの三相変圧器に400kW（遅れ力率0.8）の平衡三相負荷が接続されている。これに新たに60kW（遅れ力率0.6）の平衡三相負荷を追加接続する場合について、次の（a）及び（b）に答えよ。

　（a）コンデンサを設置していない状態で、新たに負荷を追加した場合の合成負荷の力率として、最も近いのは次のうちどれか。

　（1） 0.65　　（2） 0.71　　（3） 0.73　　（4） 0.75　　（5） 0.77

　（b）新たに負荷を追加した場合、変圧器が過負荷運転とならないために設置するコンデンサ設備の必要最小の定格設備容量〔kvar〕の値として、最も適切なのは次のうちどれか。

　（1） 50　　（2） 100　　（3） 150　　（4） 200　　（5） 300

（a）の解答

　第4図（a）のベクトル図と（7）式から合成負荷の有効電力P、無効電力Q、皮相電力S、力率cosθは、

　　　P=P₁+ P₂ =400+60=460kW

　　　Q=Q₁+Q₂=(P₁ /cosθ₁ )sinθ₁＋(P₂/cosθ₂ )sinθ₂

　　　　　　　　　=(400/0.8 )×0.6＋(60/0.6)×0.8=380kvar

　 S= =596.7kVA

　 cosθ=P / S =460/596.7=0.771

　〔答〕　(5)

（b）の解答

　第4図（b）のベクトル図と（8）、（9）式から

　変圧定格容量V=500kVAであるから、許される無効電力は、

　Q₃= =196kvar

　 コンデンサの容量Q_c=( Q₁＋Q₂)－Q₃ =380－196=184kvar

　〔答〕　184より大きく最も近いものとして(4)

（3）力率改善と損失軽減

　60kW、遅れ力率0.6の負荷が高圧配電線路に接続されている。力率を改善するために負荷と並列に電力用コンデンサを設置したところ、線路損失は48％弱減少した。設置したコンデンサの容量〔kvar〕として正しいのは次のうちどれか。ただし、負荷の電圧は一定とする。

　（1） 30　　　（2） 35　　（3） 40　　（4） 45　　（5） 50

　〔解答〕

　コンデンサ設置前の皮相電力S₁、無効電力Q₁は（5）式から、

　　　　　S₁=60/0.6=100kVA　　 Q₁=100 =80kvar

　コンデンサQ設置後の皮相電力S₂とすると、第5図のベクトル図と（13）式から、

=72kVA

=72kVA

　設置されたコンデンサの容量Qは(14)式から、

kvar

kvar

　〔答〕　線路損失は48％弱減少から(3)

　これらの問題はベクトル図を描いて対応することで短時間の回答ができる。